Отношения между понятиями. Понятия находятся в различных отношениях друг к другу

Понятия находятся в различных отношениях друг к другу. Они, прежде всего, являются сравнимыми и несравнимыми. Понятия сравнимы, если они имеют общий род. Если у понятий нет общих родовых признаков, то они несравнимы. Несравнимые понятия не вступают в какие-либо логические отношения. Сравнимые понятия делятся на совместимые и несовместимые.

Совместимые понятия делятся на три вида отношений: равнозначности, подчинения, пересечения.

Отношение равнозначности между понятиями имеет место тогда и только тогда, когда объемы этих понятий полностью совпадают. Другими словами, равнозначные понятия отсылают к одному и тому жен классу предметов, но делают это по-разному.

Отношение подчинения между понятиями имеет место тогда и только тогда, когда объем одного полностью входит в объем другого, но обратное не верно.

Отношение перекрещивания (пересечения) между понятиями имеет место тогда и только тогда, когда их объемы частично совпадают.

По несовместимости понятия делятся на три вида отношений: противоречия (контрадикторности), противоположности ( контрарности), соподчинения (координации).

Отношение противоречия (контрадикторности) между понятиями имеет место тогда и только тогда, когда они являются видами одного и того рода, притом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, не заменяя их другими признаками.

Отношение противоположности ( контрарности) между понятиями имеет место тогда и только тогда, когда они являются видами одного и того рода, притом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, заменяя признаками их исключающими.

Отношение соподчинения (координации)между понятиями имеет место тогда и только тогда когда, когда, объемы двух и более понятий исключают друг друга, но принадлежат общему родовому понятию. Это виды одного и того рода.

Отношения между понятиям можно изобразить в виде круговых схем.

Отношение равнозначности. Понятия «студент» и «учащийся высшего учебного заведения» находятся в отношении равнозначности. Если понятие

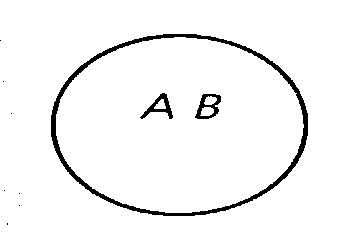
«студент» обозначим буквой А, а понятие «учащийся высшего учебного заведения» — буквой В, то отношение равнозначности между этими понятиями изобразится в виде двух совпадающих кругов (Рис. 1).

Рис. 1

Отношение подчинения. Понятия «студент» и «студент ИУБиП» находятся в отношении подчинения. Подчиняющим понятием будет «студент», подчиненным – «студент ИУБиП». Если понятие «студент» обозначим буквой А, а понятие «студент ИУБиП» - буквой В, то отношение подчинения между этими понятиями изобразиться в виде двух кругов, причем объем подчиненного понятия полностью входит в объем подчиняющего (Рис. 2).

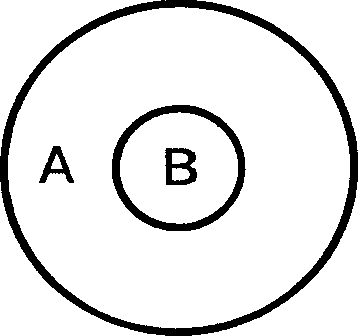
Рис.2.

Отношение перекрещивания ( пересечения). Понятия «студент» и «спортсмен» находятся в отношении перекрещивания. Если понятие «студент» обозначим буквой А , а понятие «спортсмен» - буквой В, то отношение перекрещивания между этими понятиями изобразится в виде пересекающихся двух кругов ( Рис. 3).

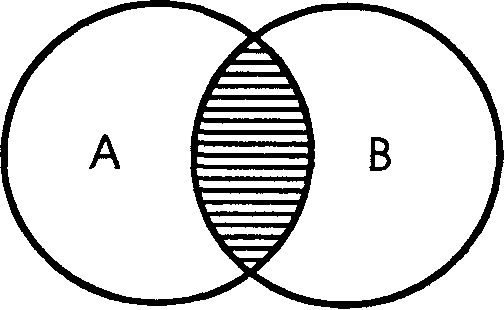
Рис. 3.

Отношение противоречия (контрадикторности). Понятия «студент» и «нестудент» находятся в отношении противоречия. Если понятие «студент» обозначим буквой А, а понятие «нестудент» - буквой не-А, то отношение противоречия между этими понятиями изобразится в виде разделенного круга (Рис.4).

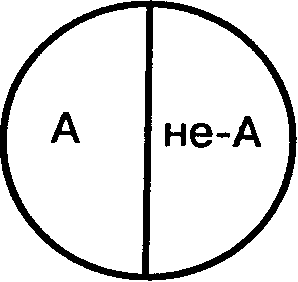
Рис.4

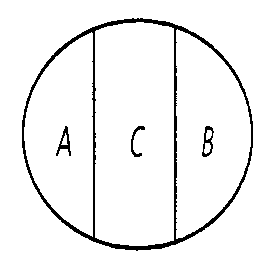
Отношение противоположности (контрарности). Понятия «белый» и «черный» находятся в отношении противоположности. Если понятие «белый» обозначим буквой А, а понятие «черный» - буквой В, то отношение противоположности между этими понятиями изобразится в виде следующего рисунка ( Рис. 5).

Рис. 5.

Отношение соподчинения (координации). Понятия «учащийся», «школьник» и «студент» находятся в отношении соподчинения. Если понятие «учащийся» обозначим буквой С, понятие «школьник» - буквой А, а понятие «студент» буквой В, то отношение соподчинения между этими понятиями изобразится в виде отдельных неперекрещивающихся кругов внутри третьего круга (Рис.6).

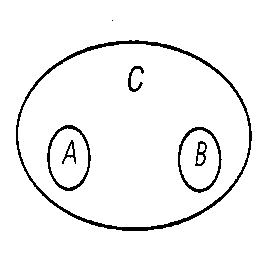
Рис. 6.

Определение.

В научной деятельности широко используется логическая операция, получившая название определения. Определение ( или дефиниция от лат. definition – определение) – это логическая операция, заключающая в придании точного смысла языковому выражению. Процедура определения решает две теоретические задачи: (1) уточняет содержание уже используемых понятий; (2) вводит в научный оборот новые понятия. Сама процедура определения наделяет предмет отличительными признаками, указывающими, с одной стороны, способ его бытия, с другой, - выделяющими и отличающими его от других предметов. Эти признаки предмета, следуя классической философской традиции, называют существенными.

Логика выделяет различные способы и правила определений, выявляет типичные ошибки, допускаемые в исследовательской деятельности, и их теоретические последствия.

В науке применяются определения различных видов. Это, прежде всего, реальные и номинальные определения. В реальных определениях на основе системы признаков осуществляется выделения предмета или класса однородных предметов в понятие. Посредством реальных определений в основном уточняется смысл используемых языковых выражений. Номинальные определения – это соглашение относительно способов употребления тех или иных языковых выражений ( понятий, терминов и т.д.).

Деление определений на реальные и номинальные – это деление по их выполняемым функциям в научном познании. По форме определения можно разделить на два вида: явные и неявные.

Явными называются определения, имеющими структуру: «Dfd ≡ Dfn» где Dfd - дефиниендум (определяемое выражение), Dfn – дефиниенс (определяющее). Знак «≡» - устанавливает логическое отношение между дефиниендумом и дефиниенсом. Это обычно отношение тождества или эквивалентности. Неявные определения такой формы не имеют.

Среди явных определений выделяют определение через род и видовое отличие, которое широко используется в социально-гуманитарных науках.

Определение через род и видовое отличие делится на:

1) атрибутивно-реляционные определения. В этих определениях видовыми отличиями выступают или свойства(атрибуты) предметов, или отношения (реляции) между ними.;

2) генетические определения. В качестве видового отличия выступает способ происхождения предмета;

3) операциональные определения, определения в которых указывается действие, с помощью которого становится возможным распознавание предмета.

К явным определениям предъявляются следующие требования:

1) правила взаимозаменяемости: при замене Dfd на Dfn (или же Dfn на Dfd) истинностное значение языкового выражения, в которую они входят, должно оставаться неизменным. Это правило соразмерности Dfd и Dfn, т.е. их объемы должны совпадать. При нарушении этого правила возникают следующие ошибки:

· «ошибка слишком широкого определения»: объем Dfn( определяющего) понятия шире Dfd (определяемого);

· «ошибка слишком узкого определения»: объем Dfn (определяющего) уже Dfd(определяемого);

· «перекрещивающееся определение»: объемы Dfd и Dfn частично совпадают;

2) в определении не должно быть «порочного круга». Нельзя определять понятие через само себя или понятие, которое, в свою очередь, определяется через определяемое понятие;

3) определение должно быть ясным ( в классической логике это требование приобретает строгою форму и предстает в качестве правила однозначности): каждому Dfd должен соответствовать

Среди неявных определений выделяют остенсивные и контекстуальные определения.

Остенсивные ( от лат. ostensio – показывание)- это разъяснение слов и словосочетаний путем непосредственного указывания на предмет.

Контекстуальные [ от лат. contextus ( тесная связь, соединение) – законченный в смысловом отношении отрывок текста.] определения – определения смысловое содержание которых следует из отрывка текста. Смысловая целостность контекста описания, установившаяся связь данного понятия с другими, уже известными, выражениями языка, позволяет выявить его содержание. Контекстуальные определения, конечно, далеки от идеала строгости, хотя имеют большое хождение в современном неклассическом дискурсе.

1.3. Лекция: Суждение

1.3.1. Общая характеристика суждения.

1.3.2 Простые суждения.

1.3.3 Отношение между суждениями по истинности.

1.3.4. Сложное суждение и его виды.