Виды имен по объему и содержанию
Если в объём имени входит только один предмет, то такое имя называют единичным.
Общее имя - это имя, в объём которого входит более одного элемента. Класс, являющийся объёмом общего имени, называют значением этого имени.
Особой разновидностью общих имен являются универсальные имена, или универсумы. Ими фиксируются все классы объектов, все элементы, исследуемые в той или иной области познания. Имена, входящие в один и тот же универсум, называются родственными.
Нулевые (пустые) имена в самом общем виде определяются как имена, объём которых не содержит ни одного элемента. Класс, не содержащий ни одного элемента, называют нулевым, или пустым.
Различают также имена описательные и собственные. Описательные имена обозначают объекты, указывая их соответствующие признаки. Собственные имена обозначают объекты путем непосредственной соотнесенности с ними, в силу того, что в культуре человеческого сообщества сложились определенные традиции, нормы именования.
Важно различать собирательные и несобирательные имена. Несобирательным называется такое имя, каждый элемент объёма которого представляет собой нечто единое, целостное. Собирательным называется такое имя, каждый элемент которого является совокупностью, собранием, объединением каких-то объектов.
Выделяют положительных и отрицательных имен. Оно базируется на том, что объекты можно охарактеризовать как по наличию, так и по отсутствию у предметов некоторых свойств. Положительным считается имя, в содержании которого указываются свойства, присущие объектам. Отрицательным считается имя, в содержании которого указываются свойства, отсутствующие у предметов.
Наконец, укажем деление имен на чёткие и нечёткие. Если имя таково, что относительно любого предмета можно точно, однозначно решить, входит или не входит этот предмет в объём данного имени, то это имя называют четким (точным, определенным) по объёму (напр., рациональное число, натуральное хозяйство, уголовная ответственность). В противном случае имя считается нечетким (неопределенным, расплывчатым, размытым, неточным) по объёму (напр., дорогой товар, молодой человек, приятная внешность).
ОТНОШЕНИЕ СОВМЕСТИМОСТИ
Имена считаются совместимыми если их объёмы хотя бы частично совпадают, т.е. эти объёмы имеют общие элементы.
Виды совместимых имён:
1) Равнообъёмными (равнозначными) считаются имена, объёмы которых полностью совпадают (рис.1)[1]. При отношении равнообъёмности имен AиB каждый предмет, обозначенный именем A,может бытьобозначен именем B, и наоборот.
2) Имена находятся в отношении подчинения, если объём одного полностью включается в объём другого, но не совпадает с ним. При этом включающеё имя называется подчиняющим, или родовым, а включенное – подчиненным, или видовым. Если имя A подчиняется имени B (рис.2), то все признаки Bприсущи содержанию имени A, и каждый предмет, обозначаемый именем A, может обозначаться именем B (но не наоборот).
3) Пересекающимися (перекрещивающимися) являются такие имена, объёмы которых лишь частично входят друг в друга. При этом некоторые предметы, обозначаемые именем A, могут обозначаться именем B, и наоборот. Если имена A и B находятся в отношении пересечения (рис.3), то предметы, входящие одновременно в объёмы имен A и B, то есть находящиеся на пересечении этих объёмов, обладают одними и теми же признаками.
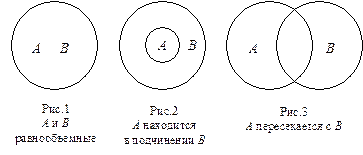
Отношения между родственными именами.
Отношение несовместимости
При отношении несовместимости в содержании одного из имен указываются признаки, исключающие признаки содержания другого имени.
Виды несовместимых имён:
1) Противоречащими называются два несовместимых имени, видовое содержание одного из которых (т.е. совокупность его видовых признаков) является отрицанием видового содержания другого. Такие имена полностью исчерпывают объём третьего, подчиняющего их имени (рис.4).
2) Соподчиненными называются такие несовместимые имена, объёмы которых в сумме составляют часть объёма некоторого подчиняющего (родового) имени. Поскольку A и B, будучи внеположенными, одновременно подчинены С, постольку их называют также внеположенными относительно С (рис. 5).
3) Противоположными называют имена, содержания которых выражают какие-либо крайние характеристики в некотором упорядоченном ряду постепенно меняющихся свойств (рис. 6).
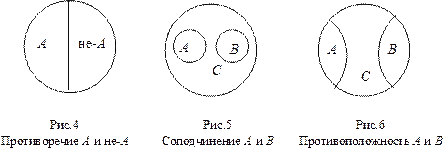
Обобщение и ограничение как операции с именами
Обобщение объема A ‑ логическая операция, в результате которой образуется имя с объемом B, содержащим в себе объем A. Иными словами, обобщить имя A ‑ значит образовать такое другое имя B (род), которое подчиняло бы себе имя A (вид). Пределом обобщения в каждом конкретном случае выступает некое универсальное имя.
Ограничение ‑ логическая операция, обратная обобщению. Она состоит в нахождении имени с объемом B, который содержится в объеме A. Ограничить объем A ‑ значит найти такое другое имя B (вид), которое находилось бы в отношении подчинения к A (роду). Пределом ограничения выступают имена, объемы которых равны одному предмету (единичные имена).
Особой разновидностью ограничения является выделение типа, или типизация. Тип ‑ это имя, которому однородные предметы соответствуют в той или иной мере. Если некоторые предметы составляют объем имени A и среди них есть такие, что безусловно (т.е. со степенью, равной 1) принадлежат к объему B, а другие обладают этим свойством в некоторой (меньшей 1) степени, то имя с объемом B представляет собой тип.
Присоединение к объему А новых предметов, тождественных со старыми по некоторому признаку, называется логической операцией расширения объема A.
Операция, обратная расширению, т. е. удаление из объема A предметов, которые тождественны с оставшимися по некоторым признакам, называется локализацией объема имени A.
Логические операции с объёмами имен не следует смешивать с мысленными переходами от части к целому и, наоборот, от целого к части. Специфика последних наиболее отчетливо выявляется при их сопоставлении с операциями обобщения и ограничения.
ОПЕРАЦИЯ ДЕЛЕНИЯ
Деление логическое– это логическая операция, посредством которой объём имени (род) распределяется по классам (видам).
Деление аналитическое – это операция, связанная с мысленным вычленением в целом его частей. Эти операции не следует смешивать.
Деление может быть классическим или неклассическим. При классическом делении как род, так и виды – имена с четким объёмом, при неклассическом они представляют собой нечеткие, расплывчатые имена, или типы.
Классическое логическое деление состоит в нахождении для имени A таких имен A1, A2, ..., An (n – конечное число), что:
а) каждый из объёмов A1, A2, ... , An находится в отношении подчинения к объёму A);
б) сумма объёмов A1, A2, ... , An равна объёму A;
в) каждая пара объёмов A1, A2, ... , An связана отношением несовместимости. При этом имя A называется делимым именем, а A1, A2, ... , An – членами деления.
В содержательном плане деление состоит в разбиении рода предметов соответственно основанию деления, т.е. особенностям (вариантам) признака, присущего данным предметам.
Возможно, что в качестве основания деления выступает признак, присущий лишь части предметов некоторого класса. В таком случае предметы делятся на те, которые этим признаком обладают, и те, которые им не обладают. Такое деление называется дихотомическим (греч. dicho – на две части, tome – сечение). В отличие от него деление по признаку, которым обладают все предметы рода и который варьируется в видах, называется политомическим греч. polis– много).
Отличие деления от расчленения базируется на различном характере отношений "целое – часть" и "род – вид".
ПРАВИЛА ДЕЛЕНИЯ
1. Правило адекватности.Деление должно быть соразмерным. Это означает, что в случае деления каждый из объёмов A1, A2,, ... , An должен быть видом объёма A, и сумма A1, A2,, ... , An должна исчерпывать весь объём A;в случае расчленениямысленное соединение частей должно быть равно целому.Отступление от этого правила ведет к ошибкам, наиболее известные из которых: "деление с лишними членами", когда некоторый из объёмов (частей) A1, A2, ... , An не является видом A (не входит как часть в целое А); "неполное деление", когда не все виды (части) делимого рода (целого) названы, и сумма объёмов членов деления меньше объёма делимого имени.
2. Правило разграниченности. Члены деления (расчленения) должны исключать друг друга, т.е. их объёмы не должны иметь общих элементов в случае классического деления, и части не должны перекрывать друг друга в случае расчленения.
3. Правило единственности основания. Деление должно производиться по одному основанию. При выполнении этого правила предметы, входящие в объём делимого имени, наделяются одним единственным признаком – тем, который выступает в качестве основания деления. Отступление от этого правила ведет к погрешности, которая называется смешением оснований.
Вместо термина "деление" иногда в качестве синонима используется термин "классификация". Классификация в узком смысле(именно в этом смысле мы будем использовать данный термин в дальнейшем) - это многоступенчатое, разветвленное деление, такое, что каждый из членов, полученный в процессе этой операции, становится предметом дальнейшего деления.
Соответственно классическому и неклассическому делению следует различать классическую и неклассическую классификацию. Последняя называется типологией.
За многоступенчатым и разветвленным расчленением пока что простого и однозначного термина не закрепилось. Эту операцию можно назвать иерархизацией.
Классификация и иерархизация подчиняются всем правилам деления. Кроме того, они имеют свои особые правила.
1. Правило последовательности. В случае классификации следует от рода переходить к ближайшим видам, а в случае иерархизации – от целого к его частям одного и того же уровня, не пропуская их. При нарушении этого правила допускаемая погрешность – «скачком в классификации (иерархизации)».
2. Правило существенности основания. Классификация (иерархизация) должна производиться по существенным признакам. Критерием существенности того или иного признака является способность обладающего им предмета служить средством решения поставленной задачи.
Частным случаем расчленения является периодизация.Её особенностью является, во-первых, указание на развитие отображаемого предмета во времени. Во-вторых, члены расчленения (периоды) отличаются своей мерой как единством качественных и количественных характеристик предмета.
ОПРЕДЕЛЕНИЕ, ИЛИ ДЕФИНИЦИЯ (ОБЩАЯ ХАРАКТЕРИСТИКА)
В логике различают прежде всего два разных смысла термина "определение". Во-первых, под определением понимается операция, позволяющая выделить некоторый предмет среди других предметов, однозначно отличить его от них. Это достигается путем указания на признак, присущий этому, и только этому, предмету. Такой признак называется отличительным (специфическим). Как мы поступаем, например, если требуется выделить квадраты из класса прямоугольников? Мы указываем на признак, присущий квадратам и не присущий другим прямоугольникам, –на равенство их сторон.
Во-вторых, определением называют логическую операцию, дающую возможность раскрыть, уточнить или сформировать смысл одних языковых выражений с помощью других языковых выражений. Так, если человек не знает, что означает слово "вершок", ему разъясняют, что вершок –это древняя мера длины, равная 4,4 см. Поскольку человеку заранее известно, что такое "древняя мера длины, равная 4,4 см", постольку для него становится ясным и понятным смысл слова "вершок".
Определение, дающеё отличительную характеристику некоторого предмета, называется реальным. Определение, раскрывающеё, уточняющеё или формирующеё смысл одних языковых выражений с помощью других, называется номинальным.
Прием установления значения языкового выражения путем его непосредственного соотнесения с обозначаемым предметом или его образом называется остенсивным определением.
В структуре определения выделяется три части:
1) определяемое имя или выражение, его содержащеё (обозначается знаком Dfd –сокращением от лат. definiendum);
2) выражение, раскрывающеё, уточняющеё или формирующеё значение определяемого имени (обозначается знаком Dfn - сокращением лат. definiens);
3) дефинитивная связка, соотносящая Dfd и Dfn по их значению (обозначается знаком º).
Формально структура определения представляется выражением: Dfd º Dfn.
ПРАВИЛА ОПРЕДЕЛЕНИЯ
1. Правило соразмерности. Dfd и Dfn должны быть равнообъёмны.
Отклонение от правила соразмерности приводит к ошибкам:
1) «слишком широкое определение» - объём Dfn больше объёма Dfd;
2) «слишком узкое определение» - объём Dfn меньше объёма Dfd;
3) «одновременно слишком широкое и слишком узкое определение» - объёмы Dfd и Dfn находятся в отношении пересечения.
4) определение через пустое имя - Dfd и Dfn оказываются несовместимыми.
2. Правило запрета порочного круга. Запрещается Dfd определять через Dfn, который, в свою очередь, определен через Dfd. Допускаемое при этом нарушение называется "порочный круг в определении". Частным случаем "порочного круга" является тавтология –повторение Dfd и Dfn (хотя бы и в иной словесной форме) без установления значения Dfd.
3. Правило однозначности. Каждому Dfn в точности должен соответствовать один единственный Dfd, и наоборот. Это правило устраняет явления синонимии и омонимии, запрещает использование метафор, художественных образов.
4. Правило простоты. Dfn должен выражаться описательным именем, характеризующим определяемые предметы лишь своими основными признаками. В противном случае определение будет избыточным. В классических определениях это правило выполняется при условии, если: а) входящий в Dfn род является ближайшим по отношению к Dfd, т.е. таким, что никакое другое имя, подчиненное роду и подчиняющеё Dfd, ранее не определено; б) в Dfn отсутствуют выражения, находящиеся в отношении следования (подчинения).
5. Правило компетентности. В Dfn могут входить лишь выражения, значения которых уже приняты или ранее определены. Отклонение от этого правила называется "определением неизвестного через неизвестное".
