Тапсырма. Көмекші программаларды қолданып программа жазыңдар.

Процедуралар

1. а санының үшінші дәрежесін есептеп, нәтижені b айнымалысына қайтаратын Power_a3(a,b) процедурасын сипаттау керек (а – ену, ал b – шығу параметрі, екеуі де нақты типті). Берілген 5 нақты санның үшінші дәрежелері осы процедура көмегімен есептелсін.

2. а санының екінші, үшінші және төртінші дәрежесін есептеп, нәтижелерді сәйкесінше b, c, d айнымалыларына қайтаратын Power_a234(a,b,c,d) процедурасын сипаттау керек (а – ену, ал b,c,d – шығу параметрлері, барлығы нақты типті). Берілген 5 нақты санның екінші, үшінші және төртінші дәрежелері осы процедура көмегімен есептелсін.

3. Оң таңбалы х және у сандарының арифметикалық (amean=(a+b)/2)және геометриялық ( 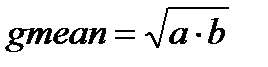) орта мәндерін есептеуге арналған Mean(x, y, amean, gmean) процедурасын сипаттау керек. (x, y – ену, ал amean, gmean – шығу параметрлері, барлығы нақты типті). Егер a,b,c,d шамалары берілген болса, онда (a,b), (a,c) және (a,d) жұптарының арифметикалық және геометриялық орта мәндері есептелсін.

4. Қабырғасының ұзындығы а тең қабырғалы үшбұрыштың периметрі (p=3×a) мен ауданын ( 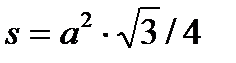)есептеуге арналған Triangle_ps(a, p, s) процедурасын сипаттау керек (a – ену, ал p, s – шығу параметрлері, барлығы нақты типті). Қабырғалары берілген үш үшбұрыштың периметрлері мен аудандары осы процедура көмегімен есептелсін.

5. Қарама-қарсы төбелерінің координаттары (x₁,y₁), (x₂,y₂) және қабырғалары координата осьтеріне параллель тік төртбұрыштың периметрі мен ауданын есептейтін Rect_ps(x₁, y₁, x₂, y_2, p, s) процедурасын сипаттау керек (x₁, y₁, x₂, y₂ – ену, ал p, s – шығу параметрлері, барлығы нақты типті). Осы процедураны пайдаланып, қарама-қарсы төбелері берілген үш тік төртбұрыштың периметрі мен ауданы есептелсін.

6. k оң бүтін санының цифрларының санын (с) және қосындысын (s)анықтауға мүмкіндік беретін DigitCountSum(k, c, s) процедурасын сипаттау керек (k – ену, ал c, s – шығу параметрлері, барлығы бүтін типті). Осы процедураны пайдаланып, мәндері берілген бес бүтін санның цифрларының саны және қосындысы есептелсін.

7. k оң бүтін санының цифрларын кері тәртіпке ауыстыратын InvertDigits(k) процедурасын сипаттау керек. (k – әрі ену, әрі шығу параметрі болатын бүтін шама). Осы процедураны пайдаланып, мәндері берілген бес бүтін санның цифрлары кері тәртіппен шығарылсын.

8. d цифрын k оң бүтін санының оң шетінен қосып жазатын AddRightDigit(d, k) процедурасын сипаттау керек (d – ену параметрі (0..9 аралығындағы бүтін сан), k – әрі ену, әрі шығу параметрі болатын бүтін шама). Осы процедураны пайдаланып, мәні берілген k санының оң шетіне d₁ және d₂ цифрлары қосып жазылсын және әр қосылу нәтижесі жеке шығарылсын.

9. d цифрын k оң бүтін санының сол шетінен қосып жазатын AddLeftDigit(d, k) процедурасын сипаттау керек (d – ену параметрі (0..9 аралығындағы бүтін сан), k – әрі ену, әрі шығу параметрі болатын бүтін шама). Осы процедураны пайдаланып, мәні берілген k санының сол шетіне d₁ және d₂ цифрлары қосып жазылсын және әр қосылу нәтижесі жеке шығарылсын.

10. х және у айнымалыларының мәндерін ауыстыратын Swap(x, y) процеду-расын сипаттау керек (х,у – әрі ену, әрі шығу параметрі болатын нақты сандар). Осы процедураны арқылы берілген a,b,c,d айнымалылары үшін (a, b), (c, d), (b, c) жұптарының мәндері ауыстырылсын және a,b,c,d айнымалыларының жаңа мәндері шығарылсын.

11. х және у мәндерінің кішісін х айнымалысына, ал үлкенін у айнымалысы-на жазатын Minmax(x,y) процедурасын сипаттау керек (x,y – әрі ену, әрі шығу параметрі болатын нақты сандар). Осы процедураны төрт рет қолдана отырып, берілген a, b, c, d шамаларының минимумы мен максимумы анықталсын.

12. Мәндері берілген a, b, c шамаларын олар өсу ретімен орналасатындай етіп ауыстыратын SortInc(a,b,c) процедурасын сипаттау керек (a, b, c – әрі ену, әрі шығу параметрі болатын нақты сандар). Сипатталған процедура арқылы a₁,b₁,c₁ және a₂,b₂,c₂ үштіктері өсу ретімен орналастырылсын.

13. Мәндері берілген a, b, c шамаларын олар кему ретімен орналасатындай етіп ауыстыратын SortDec(a,b,c) процедурасын сипаттау керек (a, b, c – әрі ену, әрі шығу параметрі болатын нақты сандар). Сипатталған процедура арқылы a₁,b₁,c₁ және a₂,b₂,c₂ жиындары кему ретімен орналастырылсын.

14. Мәндері берілген a, b, c шамаларына оң бағытты циклдық сырғуды (а-ның мәнін b-ға, b-ны – c-ға, с-ны – а-ға ауыстыру) іске асыратын ShiftRight(a, b, c) процедурасын сипаттау керек (a, b, c – әрі ену, әрі шығу параметрі болатын нақты сандар). Сипатталған процедура арқылы a₁,b₁,c₁ және a₂,b₂,c₂ жындарына оң бағытты циклдық сырғу іске асырылсын.

15. Мәндері берілген a, b, c шамаларына сол бағытты циклдық сырғуды (а-ның мәнін с-ға, с-ны – b-ға, b-ны – а-ға ауыстыру) іске асыратын ShiftRight(a, b, c) процедурасын сипаттау керек (a, b, c – әрі ену, әрі шығу параметрі болатын нақты сандар). Сипатталған процедура арқылы a₁,b₁,c₁ және a₂,b₂,c₂ жиындарына сол бағытты циклдық сырғу іске асырылсын.

Функциялар

16. х нақты саны үшін келесі мәндерді анықтайтын бүтін типті Sign(x) функциясын сипаттау керек:

-1, егер x<0 болса, 0, егер x=0 болса, 1, егер x>0 болса

Осы функция көмегімен мәні берілген a,b сандары үшін Sign(a)+Sign(b)

өрнегінің мәні есептелсін.

17. a×x²+b×x +c=0 квадрат теңдеуінің түбірлерінің санын анықтайтын бүтін типті RootsCount(a,b,c) функциясын сипаттау керек (a,b,c – нақты типті параметрлер, a≠0). Оның көмегімен коэффициенттері арқылы берілген үш квадрат теңдеудің түбірлерінің саны анықталсын. Түбірлердің саны d=b²-4×a×c дискриминантының мәні бойынша табылсын.

18. Радиусы r дөңгелектің ауданын табатын нақты типті Circle(r) функциясын сипаттау керек (r – нақты параметр). Осы функция көмегімен радиустары берілген үш дөңгелектің аудандары анықталсын. Радиусы r дөңгелектің ауданы s=p×r² формуласымен есептеледі, ал p=3.14 деп алынсын.

19. Центрлері ортақ, радиустары r₁ және r₂ шеңберлерімен шектелетін сақинаның ауданын есептейтін RingS(r₁,r₂) функциясын сипаттау керек (r₁,r₂ – нақты параметрлер, r₁>r₂). Осы функция көмегімен ішкі және сыртқы радиустары берілген үш сақинаның аудандары анықталсын. Радиусы r дөңгелектің ауданы s=p×r² формуласымен есептеледі, ал p=3.14 деп алынсын.

20. Табан қабырғасы а мен табанына түсірілген биіктігі h арқылы тең бүйірлі үшбұрыштың периметрін есептейтін TriangleP(a,h) функциясын сипаттау керек (a,h – нақты параметр). Осы функция көмегімен табан қабырғасы және оған түсірілген биіктіктері берілген үш үшбұрыштың периметрлері анықталсын. Үшбұрыштың бүйір қабырғасын табу үшін Пифагор теоремасын пайдалануға болады: b²=(a/2)²+h².

21. Бүтін a және b шамаларының арасындағы барлық бүтін сандардың қосындысын (олардың өздерімен қоса) анықтау үшін бүтін типті SumRange(a,b) функциясын сипаттау керек. Егер a>b болса, онда функция 0 мәнін қайтарады. Сипатталған функция көмегімен мәндері берілген a,b,c шамалары үшін a-дан b-ға дейінгі және b-дан c-ға дейінгі барлық бүтін сандардың қосындысы есептелінсін.

22. Нөлдік емес a және b сандарына арифметикалық амалдардың бірін орындап, нәтижесін шығаратын Calc(a,b,Op) функциясын сипаттау керек. Арифметикалық амал түрі бүтін Ор параметрі арқылы анықталады: 1 – азайту, 2 – көбейту, 3 – бөлу, өзге мәндер – қосу. Берілген a және b үшін n₁,n₂,n₃ бүтін сандары арқылы анықталатын амалдар орындалсын.

23. Нөлдік емес нақты х, у сандары арқылы берілген нүкте орналасқан координаттық ширектің нөмірін анықтайтын бүтін Quarter(x,y) функциясын сипаттау керек. Осы функция арқылы нөлдік емес координаттармен берілген үш нүктенің координаттық ширектерінің нөмірлері анықталсын.

24. Бүтін k параметрі жұп болса – TRUE, әйтпесе – FALSE сөзін қайтаратын логикалық Even(k) функциясын сипаттау керек. Сипатталған функция көмегімен 10 бүтін саннан тұратын жиындағы жұп элементтердің саны анықталсын.

25. Егер бүтін k (k>0) параметрі қандай да бір бүтін санның квадраты болса – TRUE, әйтпесе – FALSE сөзін қайтаратын логикалық IsSquare(k) функциясын сипаттау керек. Сипатталған функция көмегімен 10 бүтін саннан тұратын жиындағы квадраттардың саны анықталсын.

26. Егер бүтін k (k>0) параметрі 5-тің дәрежесі болса – TRUE, әйтпесе – FALSE сөзін қайтаратын логикалық IsPower5(k) функциясын сипаттау керек. Сипатталған функция көмегімен 10 бүтін саннан тұратын жиындағы 5-тің дәрежелерінің саны анықталсын.

27. Егер бүтін k (k>0) параметрі n-нің дәрежесі (n>1) болса – TRUE, әйтпесе – FALSE сөзін қайтаратын логикалық IsPowerN(k,n) функциясын сипаттау керек. Сипатталған функция көмегімен 10 бүтін саннан тұратын жиындағы n-нің дәрежелерінің саны анықталсын.

28. Егер бүтін n (n>1) параметрі жай сан болса – TRUE, әйтпесе – FALSE сөзін қайтаратын логикалық IsPrime(n) функциясын сипаттау керек (жай сан деп 1 және өзінен басқа бүтін бөлгіштері жоқ санды айтады) Сипатталған функция көмегімен 1-ден артық 10 бүтін саннан тұратын жиындағы жай сандардың нешеу екені анықталсын.

29. Оң бүтін k параметріндегі цифрлардың санын анықтауға мүмкіндік беретін DigitCountK(k) функциясын сипаттау керек. Осы функцияны пайдаланып, мәндері берілген бес бүтін элементтің цифрларының саны есептелсін.

30. Оң бүтін k параметріндегі n-ші цифрды қайтаруға мүмкіндік беретін DigitN(k,n) функциясын сипаттау керек (цифрлар солдан оңға қарай нөмірленеді). Егер k саынндағы цифрлар саны n-нен кем болса, функция -1 мәнін қайтарады. k₁,k₂,…,k₅ бүтін сандарының әрқайсысы үшін параметрі n (1 ≤ n ≤ 5) болатын DigitN функциясы орындалсын.

31. Егер бүтін n (n>0) параметрі палиндром болса – TRUE, әйтпесе – FALSE сөзін қайтаратын логикалық IsPalindrom(n) функциясын сипаттау керек (палиндром дем солынан да, оңынан да бірдей оқылатын сандарды айтады). Сипатталған функция көмегімен 10 бүтін саннан тұратын жиындағы барлық палиндромдар анықталсын. Функцияны сипаттау кезінде 29-шы және 30-шы есептердегі DigitCountK және DigitN функцияларын қолдануға болады.

32. Градуспен берілген d (0<d<360) бұрышының мәнін радианмен анықтайтын нақты типті DegToRad(d) функциясын сипаттау керек. Келесі қатынасты пайдалануға болады: 180°=p × радиан, мұндағы p=3.14. Анықталған функция көмегімен берілген бес бұрыштың градустық мәні радианға ауыстырылсын.

33. Радианмен берілген r (0<r<2×p) бұрышының мәнін градуспен анықтайтын нақты типті RadToDeg(r) функциясын сипаттау керек. Келесі қатынасты пайдалануға болады: 180°=p × радиан, мұндағы p=3.14. Анықталған функция көмегімен берілген бес бұрыштың радиандағы мәндері градуспен табылсын.

34. Бүтін типті n (n>0) параметрі үшін n!=1×2×…× n факториалын есептейтін нақты faсt(n) функциясын сипаттау керек (функция мәнінің нақты болу себебі – n-нің үлкен мәндері үшін «бүтін санды тасқынның» алдын алу болып табылады). Сипатталған функция көмегімен берілген бес бүтін санның факториалдары анықталсын.

35. Бүтін типті n (n>0) параметрі үшін қос факториалды есептейтін нақты faсt2(n) функциясын сипаттау керек:

n!!=1×3×5…× n, егер n – тақ болса,

n!!=2×4×6…× n, егер n – жұп болса.

(функция мәнінің нақты болу себебі – n-нің үлкен мәндері үшін «бүтін

санды тасқынның» алдын алу болып табылады). Сипатталған функция

көмегімен берілген бес бүтін санның қос факториалдары анықталсын.

36. F₁=1, F₂=1, F_k=F_k-2+F_k-1, k=3,4,… формулаларымен анықталатын F_k Фибоначчи сандарының тізбегіндегі n-ші нөмірлі элементті табатынбүтін типті Fib(n) функциясын сипаттау керек. Сипатталған функция көмегімен Фибоначчи сандарының n₁,n₂,…,n₅ нөмірлі элементтері анықталсын.

Функциялар пен процедураларға қосымша тапсырмалар

37. a^b шамасын a^b=exp(b× ln(a)) формуласымен есептейтін нақты типті Power(a,b) функциясын сипаттау керек (a,b параметрлері нақты). a≤0 жағдайда функция 0-дік мән қайтарады. Осы функцияны пайдаланып, мәндері берілген a,b,c,p шамалары үшін a^p,b^p,c^p дәрежелері есептелінсін.

38. Келесі Евклид алгоритмін қолданып, оң a және b бүтін сандарының ең үлкен ортақ бөлгішін (ЕҮОБ) табатын NOD2(a,b) функциясын сипаттау керек:

ЕҮОБ(a,b)= ЕҮОБ(b, a mod b), егер b ≠ 0 болса; ЕҮОБ(a,0)=а.