III. Аксиоматизируемые классы. Теория арифметики.

1. Аксиоматизируемые классы, критерий аксиоматизируемости. ([1, § 25], [2, § 5.2])

2. Сохранение аксиоматизируемости при взятии объединения и пересечения. ([1, § 25], [2, § 5.2])

3. Связь конечной аксиоматизируемости с сохранением аксиоматизируемости при взятии дополнения. ([1, § 25], [2, § 5.2])

4. Система аксиом арифметики Пеано. ([1, § 38], [2, § 7.5])

5. Выводимость атомарных формул и их отрицаний в арифметике Пеано. ([1, § 38], [2, § 7.5])

IV. Разрешимые и неразрешимые теории. Теорема Гёделя о неполноте.

1. Гёделевская нумерация. ([1, § 38], [2, § 7.3])

2. Теорема о рекурсивной перечислимости множества гёделевских номеров доказуемых формул. ([1, § 38], [2, § 7.3])

3. Теорема о представимости рекурсивных функций в арифметике Пеано. ([1, § 38])

4. Теорема о неразрешимости арифметики. ([1, § 38], [2, § 7.5])

5. Теорема Гёделя о неполноте. ([1, § 38], [2, § 7.5])

6. Теорема Чёрча о неразрешимости 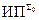. ([1, § 38], [2, § 7.5])

7. Разрешимость полной рекурсивно аксиоматизируемой теории. ([1, § 38])

8. Элементарные подсистемы, критерий элементарности подсистем. ([1, § 24], [2, § 5.1])

9. Элементарная диаграмма и ее свойство. ([1, § 24], [2, § 5.1])

10. Теоремы Лёвенгейма-Скулема. ([1, § 24], [2, § 5.1])

11. Теорема о полноте категоричной теории. ([1, § 29], [2, § 5.6])

12. Разрешимость теорий одноместных предикатов, поля комплексных чисел, плотных линейных порядков, поля вещественных чисел, векторных пространств. ([1, § 39], [2, § 8.1-8.3])

Программа практических занятий

По математической логике

Семестр

1. Понятие формулы. Таблицы истинности. Семантическая эквивалентность (2 часа). Лавров, Максимова (ЛМ), Часть 2, § 1, N 1-3, 7-10, 19-20.

2. Вывод в исчислении высказываний. Допустимые правила. Вывод основных эквивалентностей (6 часов). ЛМ, Часть 2, § 3, N 1-9, 14.

3. Приведение к нормальным формам (2 часа). ЛМ, Часть 2, § 1, N 24.

4. Контрольная работа (2 часа).

5. Приведение к совершенным нормальным формам (2 часа). ЛМ, Часть 2, § 1, N 29, 30, 32, 33, 35-40.

6. Функционально полные системы связок (2 часа). ЛМ, Часть 2, § 2, N 2-6, 8-13.

7. Исчисление высказываний гильбертовского типа (4 часа). ЛМ, Часть 2, § 3, N 17-40.

8. Контрольная работа (2 часа).

9. Множества и операции над ними. (2 часа). ЛМ, Часть 1, § 1.

10. Декартово произведение. Отношения и функции (2 часа). ЛМ, Часть 1, § 2, N 1-27.

11. Специальные бинарные отношения (4 часа). ЛМ, Часть 1, § 3, N 6-11, 26-31, 34-42; § 5, N 30-43.

12. Мощность множества (4 часа). ЛМ, Часть 2, § 4, N 7-36; § 6, N 8, 9.

Семестр

1. Понятие терма и формулы данной сигнатуры. Запись свойств на языке первого порядка (4 часа). ЛМ, Часть 2, § 4.

2. Истинность и выполнимость. Приведение к предваренной нормальной форме (4 часа). ЛМ, Часть 2, § 5, N 7-19, 30-37, 42.

3. Выводы в исчислении предикатов (4 часа). ЛМ, Часть 2, § 6, N 1-10, 14-30, § 7, N 1.

4. Локальная теорема Мальцева (4 часа). ЛМ, Часть 2, § 7, N 12-17; § 9, N 1-3, 5, 7, 8.

5. Фильтрованные произведения (4 часа). ЛМ, Часть 2, § 8, N 1-16; 29, 30, 44-51.

6. Контрольная работа (2 часа).

7. Примитивно рекурсивные и частично-рекурсивные функции (4 часа). ЛМ, Часть 3, § 1, N 1-32.

8. Машины Тьюринга. Функции, вычислимые на машинах Тьюринга (2 часа). ЛМ, Часть 3, § 2, N 1-10.

9. Рекурсивные и рекурсивно перечислимые множества. (2 часа). ЛМ, Часть 3, § 3, N 1-29.

10. Рекурсивно аксиоматизируемые, разрешимые и неразрешимые теории (2 часа). ЛМ, Часть 2, § 7, N 13-17.

11. Формальная арифметика. Представимость рекурсивных функций (2 часа). ЛМ, Часть 2, § 7, N 18-37.

ОСНОВНАЯ ЛИТЕРАТУРА

1. Ершов Ю.Л., Палютин Е.А. Математическая логика. – М.: Наука, 1979, 1987; СПб.: Лань, 2004, 2005, 2006.

1. Ершов Ю.Л., Палютин Е.А. Математическая логика. – М.: ФИЗМАТЛИТ, 2011.

2. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука, 1975, 1984, или М.: ФИЗМАТЛИТ, 1995, 2001, 2004, 2006.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Гончаров С.С. Счетные булевы алгебры и разрешимость. – Новосибирск: Научная книга, 1996.

2. Гончаров С.С., Ершов Ю.Л. Конструктивные модели. – Новосибирск: Научная книга, 1999.

3. Ершов Ю.Л. Проблемы разрешимости и конструктивные модели. – М.: Наука, 1980.

4. Ершов Ю.Л. Определимость и вычислимость. – Новосибирск: НИИ МИОО

НГУ, Научная книга, 1996 или М.: Экономика, 2000.

5. Кейслер Г., Чэн Ч.Ч. Теория моделей. – М.: Мир, 1977.

6. Куратовский К., Мостовский А. Теория множеств. – М.: Мир, 1970.

7. Мальцев А.И. Алгоритмы и рекурсивные функции. – М.: Наука, 1965, 1986.

8. Мальцев А.И. Алгебраические системы. – М.: Наука, 1970.

9. Мендельсон Э. Введение в математическую логику. – М.: Наука, 1971, 1984.

10. Непейвода Н.Н. Прикладная логика. – Новосибирск: Изд-во НГУ, 2000.

11. Новиков П.С. Элементы математической логики. – М.: Наука, 1973.

12. Роджерс Х. Теория рекурсивных функций и вычислимость. – М.: Мир, 1972.

13. Соар Р. Вычислимо перечислимые множества и степени. – Казань: Казанское мат. общество, 2000.

14. Справочная книга по математической логике / Под ред. Дж. Барвайса. – М.: Наука, 1982. Т. 1–4.

15. Судоплатов С.В., Овчинникова Е.В. Дискретная математика. – М.: Юрайт, 2016.

16. Судоплатов С.В., Овчинникова Е.В. Математическая логика и теория алгоритмов. – М.: Юрайт, 2016.

17. Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. – М.: Наука, 1983.