Онятие о нечетких множествах и лингвистических переменных

4. ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ ОБРАБОТКИ

ИНФОРМАЦИИ НА ОСНОВЕ НЕЧЕТКОЙ ЛОГИКИ

ведение

В 1965 г. появилась статья Л. Заде «Fuzzy Sets», которая положила начало теории нечетких множеств (НМ). Основная идея Заде: человеческий способ рассуждений, опирающийся на естественные языки, не может быть описан в рамках традиционных формализмов. Программа Л. Заде состояла в построении новой математической дисциплины, в основе которой лежала бы не классическая теория множеств (чётких множеств), а теория нечетких множеств (НМ). Тогда можно построить нечеткие аналоги всех основных математических понятий и создать необходимый формальный аппарат для моделирования человеческих рассуждений и человеческого способа решения задач.

При помощи НМ можно формально определить неточные и многозначные понятия, такие как «высокая температура», «молодой человек», «высокая скорость» и т.п.

Суть нового подхода к анализу сложных систем и процессов принятия решений, получившего название нечеткой логики (Fuzzy Logic), заключается в следующем:

вместо обычных числовых переменных или в дополнение к ним используются «лингвистические» переменные;

простые отношения между переменными описываются с помощью нечетких высказываний;

сложные отношения описываются нечеткими алгоритмами.

Выделяют два основных подхода к формализации нечеткости.

1. Подход. НМ образуется путем введения обобщенного понятия принадлежности, т.е. расширения множества (0, 1) значений характеристической функции до континуума [0, 1]. Это означает, что переход от полной принадлежности объекта классу (множеству) к полной его непринадлежности происходит не скачком, а плавно, постепенно, причём принадлежность элемента множеству выражается числом из интервала [0, 1]. Таким образом, НМ можно записать в виде

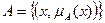, (4.1)

где 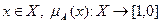– функция принадлежности.

2. Подход. Всякое НМ можно разложить по множествам уровня (теорема декомпозиции):

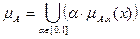, где

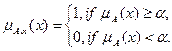
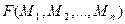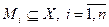То есть нечеткость выражается с помощью набора иерархически упорядоченных чётких множеств. Следовательно, для конечного числа n градаций рассматриваемого свойства n –нечёткое множество задается через n –ку обычных множеств , где и .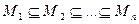

Для бесконечного числа градаций имеем бесконечное семейство множеств 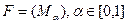, т.е. отображение вида 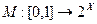, где любому числу (индексу) 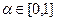ставится в соответствие чёткое подмножество множества Х.

Тогда размытость моделируется отображением М из класса функций

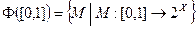со свойствами:

а) М(0)=Х; б) ;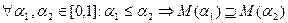

и соответствующими операциями над ними.

Связь между первым и вторым представлениями НМ устанавливается теоремой представления, согласно которой классы F(X) (класс функций первого представления) и 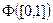изоморфны относительно операци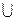й и .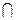

онятие о нечетких множествах и лингвистических переменных

Рассмотрим более подробно определение НМ вида (4.1). Перед формулированием определения необходимо задать область рассуждений, то есть четкое множество Х, из элементов которого формируется НМ.

Определение НМ. Нечетким множеством А в некоторой области рассуждений Х (т.е. 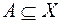) называется множество пар

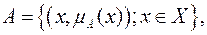
где 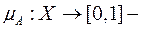функция принадлежности нечеткого множества А.

Функция 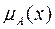приписывает каждому элементу 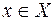степень его принадлежности к НМ А. При этом может быть три случая:

1) 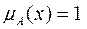при полной принадлежности элемента х к нечеткому множеству А, т.е. ;

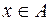2) 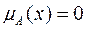при отсутствии принадлежности элемента х к нечеткому множеству А, т.е. ;

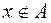3) 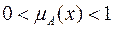при частичной принадлежности элемента х к нечеткому множеству А.

В литературе используется описание нечеткого множества как в виде множества пар, так и в символьном виде. Если множество Х имеет конечное число элементов 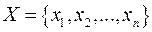, то нечеткое множество 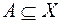часто записывается в виде

.

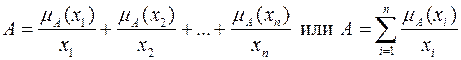Символьная запись 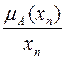означает пару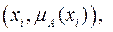 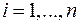. Символ «+» не означает операцию сложения, а интерпретируется как множественное суммирование пар. Возможен и табличный способ задания нечеткого множества.

Если множество Х имеет бесконечное число элементов, то нечеткое множество 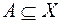часто записывается в виде

.

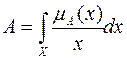В этом случае функция принадлежности 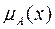обычно задается графически или в виде аналитической зависимости.

Рассмотрим несколько примеров.

Допустим, что при измерении некоторой величины ошибка составляет 10%, например, измеренное напряжение х = 10В, а ошибка составляет 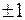В. Тогда переход от четкого значения х = 10 к нечеткому множеству х = «приблизительно 10» может быть представлен, как показано на рис. 4.1.

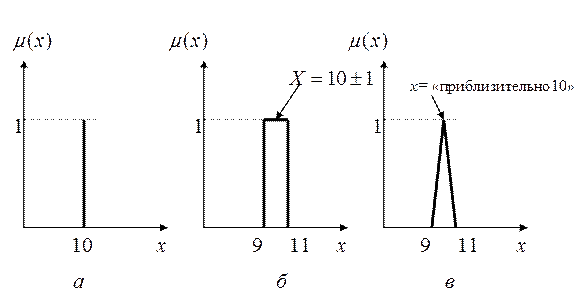
Рис. 4.1.

Функция принадлежности 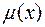, приведенная на рис. 4.1.в описывается выражением

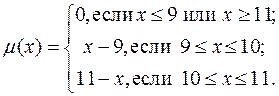(4.1)

Допустим, что Х – множество натуральных чисел. Определим понятие множества натуральных чисел, «близких числу 10». Это можно сделать с помощью следующего нечеткого множества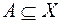

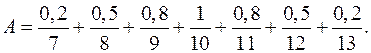
Нечеткие множества натуральных или действительных чисел, «близких числу 10», можно записать различными способами. Например, вместо функции принадлежности вида (4.1) можно использовать выражение

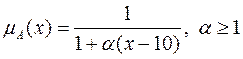(4.2)

или

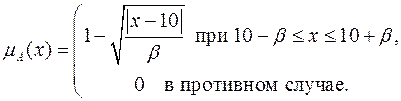(4.3)

Параметры α и β определяют степень нечеткости понятия чисел, «близких числу 10». На рис.4.2 представлены две функции принадлежности вида (4.2) и (4.3) при .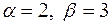

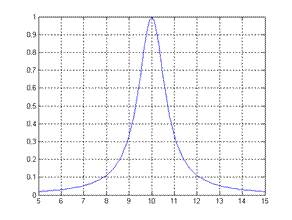
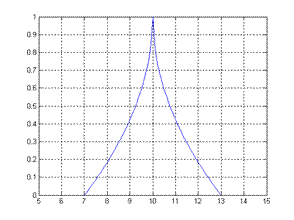
Рис. 4.2.

Выбор (или задание) функции принадлежности, а также её смысл в каждом конкретном случае является неоднозначным и во многом определяется мнением эксперта. Наиболее распространенным является мнение, что 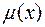может рассматриваться как «субъективная вероятность» или как «коэффициент уверенности» эксперта в том, что элемент х принадлежит множеству А.

Процесс перехода от четкого (т.е. измеренного) значения x к его нечеткой интерпретации называется фазификацией (fuzzification), например, от х = 10 к х = «приблизительно 10» (см. рис. 4.1).

Одним из ключевых понятий нечеткой логики является понятие лингвистической переменной, суть которого состоит в том, что конкретные значения числовой переменной х обычно подвергается субъективной оценке человеком, причем результат такой оценки выражается на естественном языке. Например, переменная «Скорость движения автомобиля» может характеризоваться одним из кратких словесных описаний (термов): «малая скорость», «средняя скорость», «большая скорость». Каждый терм может рассматриваться как наименование (символ, label) некоторого нечеткого подмножества в составе полного множества значений х.

Переменные, значения которых являются термы (слова, фразы, предложения), выраженные на естественном языке, называют лингвистическими переменными (linguistic variables).

Например, лингвистическая переменная «Скорость движения автомобиля» характеризуется тремя значениями, т.е. тремя нечеткими подмножествами: 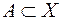для терма «малая скорость», 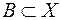для терма «малая скорость», 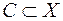для терма «малая скорость», функции принадлежности которых показаны на рис. 4.3, область рассуждений 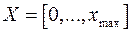, где 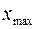– величина максимальной скорости.

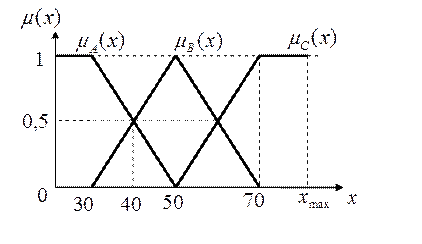
Рис. 4.3.