Расчет корреляционной функции по экспериментальным данным

Пусть стационарный случайный процесс задан одной реализацией (рис.62). Промежуток времени наблюдения процесса Т делим на N малых интервалов D так, чтобы функция x(t) мало изменялась на протяжении интервала D. T=ND. Будем придавать t и t дискретные значения, кратные D: t=nD, n=1,2,...; t=mD, m=0,1,2,....

Обозначим: R(t) = R(mD) = R(m), x(t) = x(nD) = x_n, x(t+t) = x(nD+mD) = x_n+m.

Тогда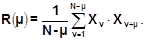

Так, 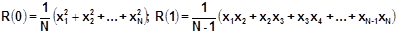и т.д.

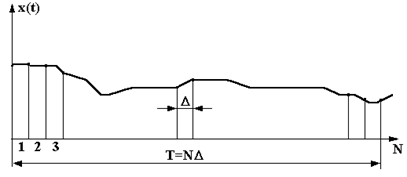
Рис.62

Спектральная плотность стационарного случайного процесса

Пусть функция x(t) на любом конечном интервале удовлетворяет условиям Дирихле и, кроме того, интеграл 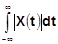сходится, тогда функцию X(t) можно представить в виде

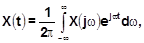(6)

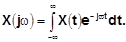где (7)

Формула (6) называется «обратное преобразование Фурье» или интеграл Фурье, а формула (7)- «прямое преобразование Фурье». Функция X(jv) называется изображением Фурье функции времени x(t).

Интеграл Фурье позволяет представить непериодическую функцию в виде бесконечной суммы гармонических составляющих с непрерывным спектром частот. X(jw) представляет собой спектральную плотность амплитуд или частотный спектр функции X(t).

Рассмотрим энергетическую форму интеграла Фурье. Пусть имеется некоторая функция (например, случайная) времени X(t).

Имеем:

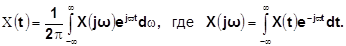
Рассмотрим выражение

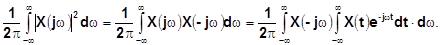
Меняем порядок интегрирования:

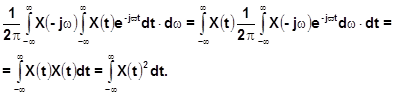
Итак,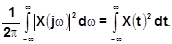

Эта формула выражает энергетическую форму интеграла Фурье и называется формулой Релея. Правая часть представляет собой величину, пропорциональную энергии рассматриваемого процесса. Например, если x(t) представляет собой напряжение на резисторе 1 Ом, то 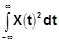представляет собой энергию, выделенную на этом сопротивлении, за бесконечно большой промежуток времени -¥<t<+¥.

Таким образом, для нахождения энергии рассматриваемого процесса за бесконечный интервал наблюдения с равным основанием можно интегрировать квадрат функции времени в интервале -¥<t<+¥ или интегрировать квадрат модуля изображения Фурье по всем частотам от -¥ до +¥.

Перейдем к средней мощности процесса. Ее можно получить, если поделить энергию процесса на интервал наблюдения.

Тогда

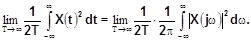
Левая часть представляет собой средний квадрат X(t).
Величина

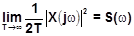
называется спектральной плотностью мощности или просто спектральной плотностью стационарного случайного процесса. Очевидно,

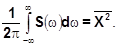
Интегрирование по всем частотам от -¥ до +¥ S(w) дает средний квадрат функции времени X(t). По физическому смыслу спектральная плотность есть величина, пропорциональная средней мощности процесса в интервале частот от w до w+dw.

S(w) является четной функцией частоты, т.к. 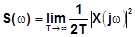.