Тема: Статистическое изучение взаимосвязей
А1. В основу непараметрических методов положен:
· принцип нумерации значений статистического ряда
А2. Если линейный коэффициент корреляции равен +1, то это говорит:
· Прямая связь
А3. Если линейный коэффициент корреляции равен 0, то это говорит:
· то он показывает полное отсутствие связи.
А4. Если линейный коэффициент корреляции равен -1, то это говорит:
· обратная
А5. Если расчетное значение хи-квадрат критерия Пирсона больше теоретического, то: гипотеза о том, что эмпирические данные можно описать теоретической функцией распределения:
· отклоняется
А6. Если расчетное значение хи-квадрат критерия Пирсона меньше теоретического, то: гипотеза о том, что эмпирические данные можно описать теоретической функцией распределения:
· принимается
А7. Если эмпирическое корреляционное отношение равно 0, то:
· то группированный признак не оказывает влияния на результативный
А8. Если эмпирическое корреляционное отношение равно 1, то:
· то результативный признак изменяется только взависимости от признака, положенного в основание группировки
А9. Коэффициент детерминации может принимать значения в пределах:
· от 0 до 1
А10. Критерий согласия Колмогорова:
· применяется для проверки статистических гипотез о законе распределения с известным видом распределения и известными параметрами.; используется для того, чтобы определить, подчиняются ли два эмпирических распределения одному закону, либо определить, подчиняется ли полученное распределение предполагаемой модели.
· 
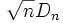
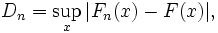
А11. Критерий согласия Пирсона:
· наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.
· 
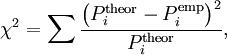где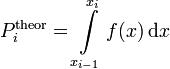 
— предполагаемая вероятность попадения в i-й интервал, 
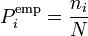— соответствующее эмпирическое значение, ni — число элементов выборки из i-го интервала
А12. Линейный коэффициент корреляции может принимать значения:
· -1 +1
А13. Минимальное количество данных, необходимое для получения надежных оценок должно быть не менее:
· 30 -40 наблюдений
А14. Минимальное количество данных, необходимое для статистической обработки должно быть не менее:
· 5-8 наблюдений
А15. Регрессионная модель называется многопараметрической, если:
· Переменная зависит от нескольких независимых переменных
А16.Регрессионная модель называется однопараметрической, если:
· Зависит от одной переменной
А17. Эмпирическое корреляционное отношение может принимать значения:
· От 0 до 1
А18.Эмпирическое корреляционное отношение можно определить как: А19.Эмпирическое корреляционное отношение определяют как:
· Это корень квадратный из эмпирического коэффициента детерминации. В свою очередь эмпир коэф детерм – для межгрупповой дисперсии в общей дисперсии
η=√σ2/σ2общ
ВАРИАНТ 1
Часть Б.
Б1. Имеются данные о группировке предприятий по стоимости основных средств:
| Группы предприятий по стоимости основных средств, млн. руб. | Число предприятий в группе, шт. |
| До 10 | |
| 10 – 14 | |
| 14 – 18 | |
| 18 – 22 | |
| 22 – 26 | |
| 26 и более |
Определить средний размер основных средств на одно предприятие. Ответ дать с точностью до 0,1.
Ответ: 19
Б2. Имеются следующие данные о затратах на производство продукции и ее себестоимости по группе предприятий:
| Предприятие | 2005 год | |
| Затраты на производство продукции, тыс. руб. | Себестоимость единицы продукции, тыс. руб. | |
| Завод 1 | ||
| Завод 2 | ||
| Завод 3 |
Определите среднюю себестоимость единицы продукции по трем заводам за 2005 год. Ответ дать с точностью до 0,1.
Ответ: 32,5
Б3. Имеются данные о группировке предприятий по стоимости основных средств:
| Группы предприятий по стоимости основных средств, млн. руб. | Число предприятий в группе, шт. |
| До 10 | |
| 10 – 14 | |
| 14 – 18 | |
| 18 – 22 | |
| 22 – 26 | |
| 26 и более |
?Определите моду и медиану. Ответ дать в целых числах. Ответ: Мо=19,3; Ме=18,5
ВАРИАНТ 2
Часть Б.
Б1. Имеются следующие данные по предприятиям, выпускающим одноименную продукцию:
| Номер предприятия | 2005 год | |
| Количество выпущенной продукции, т. шт. | Себестоимость единицы продукции, тыс. руб. | |
Определить среднюю себестоимость единицы продукции по трем предприятиям за 2005 год. Ответ дать с точностью до 0,1.
Ответ: 32,5
Б2. Имеются следующие данные о затратах на производство продукции и ее себестоимости по группе предприятий:
| Предприятие | 2005 год | |
| Затраты на производство продукции, тыс. руб. | Себестоимость единицы продукции, тыс. руб. | |
| Завод 1 | ||
| Завод 2 | ||
| Завод 3 |
Определите среднюю себестоимость единицы продукции по трем заводам за 2005 год. Ответ дать с точностью до 0,1.
Ответ: 32,5
Б3. Имеются данные о группировке рабочих предприятия по уровню месячной заработной платы:
| Группы рабочих по уровню месячной заработной платы, тыс. руб. | Число рабочих в группе, чел. |
| До 500 | |
| 500 – 550 | |
| 550 – 600 | |
| 600 – 650 | |
| 650 – 700 | |
| 700 и более |
Определите моду и медиану. Ответ дать в целых числах
Ответ: Ме=600; Мо=611,36