Рубые погрешности и критерии их оценки

1. МНОГОКРАТНЫЕ ИЗМЕРЕНИЯ И ИХ ОБРАБОТКА

Цель – рассмотрение основных понятий и изуче­ние алгоритма обработки многократных измерений.

В общем видеалгоритм обработки многократных измерений состоит из следующих шагов:

1.Анализ априорной информации; выявление известных систематических погрешностей и определение поправок С_i

2.Получение n независимых значений отсчёта 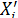по основному уравнению измерений.

3.Внесение поправок и получение n независимых значений результата наблюдения как .

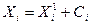4. Оценка среднего значения результата измерения .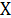

5.Оценка среднего квадратического отклонения результата наблюдения s_x.

6. Оценка среднего квадратического отклонения результата измерения .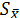

7.Выявление результатов, содержащих грубые погрешности и исключение их; повторный расчёт оценок (возвращение к пункту 4).

8. Проверка нормальности распределения результатов наблюдения.

9.Определение доверительных интервалов случайной погрешности.

10. Определение границ неисключённой систематической погрешности Θ результата измерений.

11. Определение доверительной границы погрешности результата измерения.

12. Запись результата измерения в виде доверительного интервала с указанием вероятности и размера единицы измеряемой ФВ, например, в виде: 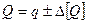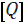; Р=0,95..

бщие сведения

Метрологический анализ многократного измерения показывает, что главной его особенностью является получение и использование большого объема апостериорной измерительной информации. Это не означает, что необходимость в анализе априорной информации отпадает. Такой анализ обязательно предшествует многократному измерению и преследует те же цели, что и при однократном измерении, но с той разницей, что при многократном измерении распределение вероятности результата измерения устанавливается экспериментально. После анализа априорной информации и тщательной подготовки к измерению получают n независимых значений отсчета. Все значения отсчёта х', независимо от способа их получения, переводятся затем в показания 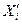, в которые вносятся поправки С_i.

Весь массив экспериментальных данных:

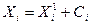; i 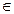(1,…n) (1.1.1)

характеризует результат измерения X. Он может быть также описан с помощью функции распределения вероятности X.

Но нужно проверить, не было ли допущено ошибок при получении отдельных значений результата измерения.

Оценки числовых характеристик законов распределения вероятности случайных чисел или величин, изображаемых точкой на числовой оси, называются точечными, интервалом — интервальными. Примером последних служат доверительные интервалы. В отличие от самих числовых характеристик оценки являются случайными, причем их значения зависят от объема экспериментальных данных, а законы распределения вероятности - от законов распределения вероятности самих случайных чисел или значений измеряемых величин.

Оценки должны удовлетворять трём требования: быть состоятельным, несмещёнными и эффективными.

· Состоятельной называется оценка, которая сходится по вероятности к оцениваемой числовой характеристике.

· Несмещённойявляется оценка, математическое ожидание которой равно оцениваемой числовой характеристике.

· Эффективной называют ту из нескольких возможных несмещённых оценок, которая имеет наименьшую дисперсию.

Математическое ожидание среднего арифметического:

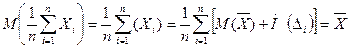(1.1.2)

где 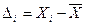– отклонение значений результатов от среднего.

Дисперсия среднего арифметического для нормального распределения и близкого по форме к нему:

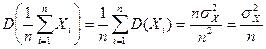(1.1.3)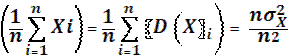

рубые погрешности и критерии их оценки

Под грубымипонимают погрешности, приводящие к явному искажению результата. Наличие грубых погрешностей определяет качество проведённых изменений. Существует несколько критериев оценки грубых погрешностей. Все они основаны на расчёте величины 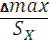_max / S_x, где ∆_max –максимальное по модулю значение разности 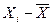, а S_x- стандартное отклонение. Дальше полученное значение сравнивается с тем или иным численным значением критерия.

Критерий «трёх сигм»

В этом случае должны быть отброшены все результаты измерений, отклонения которых от среднего арифметического превышает 3S_x, причём суждение о дисперсии генеральной совокупности 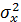делают по оставшимся результатам измерений.

Пусть X_1, Х₂, ...X_к...Х_n— ряд результатов измерений где Х_k — результат измерений, в котором предполагают наличие грубой погрешности.

1.Вычисляют 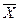по формуле cреднего арифметического п-1 членам ряда, то есть без учёта Х_k:

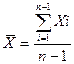(1.2.1)

2.Для нахождения критерия «трёх сигм» 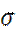получают, рассчитывая среднее квадратическое отклонение по формуле:

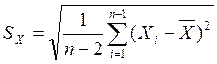(1.2.2)

Также без учёта X_k.

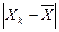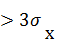3. Результат измерений X_k должен быть отброшен, если > 3σ_х или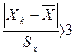

Метод рекомендуется применять при числе измерений n в интервале от 25 до 100.

Метод вычисления максимального относительного отклонения (критерий v_a).

Для проверки гипотезы об отсутствии грубых погрешностей при различных доверительных вероятностях α и числе измерений, недостаточном для надёжного определения 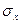(т.е. n ≤25)можно воспользоваться также критерием v_α (таблица 6 приложения).Расчётное значение v,которое не должно по принятой гипотезе превышать критического, определяют как:

или v= 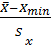(1.2.3)

Здесь: S_x- среднее квадратическое отклонение, вычисляемое с учётом всех результатов наблюдения, включая проверяемый, по формуле

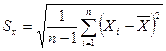(1.2.4)

а 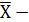среднее арифметическое( оценка истинного значения), также по всем полученным результатам

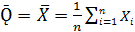(1.2.5)