Множество: референтность и дистанционная референтность

Открытой остается такая проблема для теории множеств: множество представляет собой множество объектов, где свойства нечто другое, или множество свойств, где совокупность объектов нечто другое? Если мы говорим о множестве некоторых свойств, являющихся полной совокупностью свойств некоторого объекта, то в каком отношении находятся объект и эта совокупность? Как допустимо различить свойства объекта и свойства свойств объекта? Являются ли последние такими же свойствами объекта как и первыми, или же они нечто иное? И, самое главное, может ли это отношение быть проинтерпретировано в существующей абстрактной теории множеств, или мы должны строить принципиально другую теорию?

С другой стороны, множество, которое объединяется объекты с общим свойством, выделяется как класс. И во всех изложениях определения «класс» вы встретите компромисс: ну мы же понимаем, что всегда допустимо найти некоторое свойство, но в данном случае, мы понимаем, что это разные объекты. И с этим компромиссом никак нельзя согласиться. Дело в том, что какие вы бы общности не объединили в множество, они вполне могут представлять собой класс, как минимум по тому свойству, что объединены на этом листе бумаги. И вот проблема, которую формулирует Борхес в работе «Аналитический язык Джона Уилкинса»: достаточно ли включения в классификацию (у Борхеса приводится классификация животных) для того, чтобы некоторую совокупность рассматривать как интуитивно понятную совокупность? Из этой проблемы вышла целая книга Фуко «Слова и вещи».

Проблему, которая возникает при объединении некоторых объектов в класс, можно сформулировать следующим образом. Где должна быть установлена (проинтерпретирована) актуальность (виртуальность) общего свойства объектов класса: в формальной записи или вне ее? Насколько эта актуальность (виртуальность) должна быть очевидной при объединении этих объектов в класс? Является ли дополнительный комментарий актуальности (виртуальности) общего свойства класса входящим в формальную запись, или формальная запись может подвергаться преобразованиям без учета ее дополнительного комментария? Таким образом вопрос о классе объектов это вопрос о месте актуальности (виртуальности) общего свойства класса.

По отношению к сформулированному Кантором пониманию мощности предложим следующее замечание: если мы возьмем бесконечное множество некоторых объектов и их свойств и соотнесем их с другим бесконечным множеством объектов и их свойств, будет ли мощность этих множеств одинаковой даже в том случае, если подмножества свойств могут быть разномощными?

Очевидно дело здесь не в рассмотрении, а в том, в чем обвиняли интуиционисты Кантора: перенос на бесконечные (трансфинитные) множества правил, присущих конечным (финитным) множествам неизбежно ведет к антиномиям. Мы улавливаем название такого оперирования: завершенная бесконечность или актуальная бесконечность. Актуальность, употребляемая в терминах теории множеств, означает, что некоторое отношение каждый раз подразумевалось в комментарии, участвовало в содержании формальной записи, но не отражалось в этой же формальной записи.

Именно понимание актуальности в теории множеств при обращении бесконечности в завершенную бесконечность и будет оспорена в ТВ. В связи с излагаемым нами пониманием полей актуальности, актуальной структуры, мы можем уточнить, что множество представляет собой актуальную структуру, структуру с единым полем актуальности. Причем, в теории множестве речь преимущественно идет именно об актуальности, а не о виртуальности — то есть не о конструктивных структурах. Там же где конструктивные (виртуальные) структуры, как например концептуальные объекты или имена начинают объединяться в совокупности наравне с истолковательными (актуальными) структурами, там теория множеств перестает работать, порождая парадоксы.

Теория множеств интерпретирует актуальную бесконечность. Бесконечность же должна быть расширена в своем понимании: структурная бесконечность суть не бесконечность перечня объектов или их атрибутов, но бесконечность «структурного погружения в объект и структурной надстройки над объектом», то есть бесконечность структурной глубины внутри каждого объекта (свойство, свойство свойства, свойство свойства свойства и т.д.) и бесконечность надобъектов в надструктуре объекта. Структурная бесконечность суть виртуальная бесконечность. Так возникает представление о структурном континууме как континууме, объединяющем актуальную и виртуальную бесконечность — в их контрафлексивном сопоставлении.

Размерность суть структурная глубина в некоторой дирекциональной дистанции одного или каждого элемента связности. Связность суть структурный горизонт, состоящий из элементов одной и той же размерности. Разные размерности порождают разные ряды односвязностей. Разные связности порождают разные ряды одноразмерностей. Референция (референтность) суть установленное влияние (взаимодействие) разных односвязностей. Дистанционная референция (референтность) суть установленное влияние (взаимодействие) дистанционно-удаленных уровней структуры далее одной связности и/или размерности. Разноуровневость это разноразмерность и/или разносвязность. Если дистанционная референция (референтность) — отношение между разноуровневыми элементами, множествами или реальностями, то структурность (трансструктурность) внутреннее отношение элемента, множества или реальности.

Мы предполагаем, что введение представления о виртуальной бесконечности корректирует понимание гипотезы Ходжа (гипотезы об инвариантах), где равенство множеств определяет равенство их инвариантов, и равенство инвариантов гипотетически определяет равенство их множеств. Инвариант таким образом оказывается связан с актуальной бесконечностью, то есть с актуально связанными представлениями об одноразмерности и односвязности множества. Виртуальная бесконечность разрывает связь связности и размерности, и устанавливает разные связности и разные размерности.

Таким образом если инварианты разных множеств мы рассматриваем с точки зрения разноразмерностей и разносвязностей, то мы в принципе не можем уравнивать дистанционно-референтные множества, но можем лишь осуществлять их референцию и референтность как реальностей на том или ином уровне дирекционально-дистанционной глубины. Точно также мы не можем уравнивать трансструктурные множества. Любой выход за пределы одноразмерного и односвязного множества уничтожает инвариантность. То есть виртуальность неинвариантна.

Множество тем самым является либо множеством свойств, либо множеством объектов, но не тех и других одномножественно. При этом мы будем подозревать, что не множество является более общим выражением, где класс — лишь частный случай, а класс является более общим выражением, где множество как отдельное понятие является лишним. В то же время с точки зрения теории типов два типа в ТВ разнесены в разные реальности и между ними устанавливаются дирекциональные отношения, как это было в теории Куайна, но это отношение операционализируется и становится подверженным анализу (речь идет об релевантности и типах референтности).

По существу это уже предполагает внесение релевантности в определение множества, что только формально противоречит изначальной посылке Кантора — рассматривать в принципе любые абстрактные общности. Ибо любая совокупность это релевантная совокупность.

Актуальное (виртуальное) множество в ТВ может быть рассмотрено как класс, то есть как совокупность объектов, имеющих одно или несколько общих свойств. А вот трансактуальное (трансвиртуальное) множество в ТВ может быть рассмотрено как множество объектов, которые событийно относятся к некой структуре, и для которых событие между ними ведет к изменению аспектов (атрибутов) за пределами актуальности (виртуальности) данной совокупности, независимо от того, является ли какой-нибудь из аспектов (атрибутов) общим при создании множества. Такое актуально-виртуальное установление трансактуального (трансвиртуального) множества привносит совершенно новое содержание — независимость от содержания свойств, предварительно определенных. Принадлежность к одной структуре не предполагает непосредственную близость объектов, входящих в множество, она предполагает лишь наличие экспериментально подтвержденного однособытийным взаимодействием элементов, объединяемых на этом основании в множество — как реальность, то есть общность нормирования. Основания для объединения некоторых объектов в актуальную (виртуальную) совокупность могут быть вдалеке от самой совокупности — в затухающей актуальности (виртуальности).

Причем мы рассматриваем именно трансактуальное (трансвиртуальное) множество, а не трансструктурное, так как трансструктурность предполагала бы отнесение элементов множества к структурным элементам, а это не так. Элементы множества — объекты, поэтому между ними для довиртуальной логики существует только отношение трансактуальности.

В конечном счете класс в логике отождествляют с множеством именно потому, что оказалось всегда допустимым найти общее свойство для любой совокупности (релевантность), безотносительно к их референтности, то есть взаимодействию свойств. Релевантность порождает множество, референтность — класс, если мы допускаем их в в одной и той же реальности, то есть в одном и том же нормировании. Актуальное (виртуальное) множество есть множество референтных объектов, референтность которых фиксируется в их событийном взаимодействии, где событие имеет не удаленное происхождение, а происходит непосредственно между ними, то есть в пределах актуальной (виртуальной) структуры и вызывает изменение аспектов (атрибутов) этих объектов. ТВ различает дистанционно-референтные (трансактуальные и трансвиртуальные) и актуальные (виртуальные) множества.

Более того, некоторые явления, находящиеся за горизонтом актуальности (виртуальности) могут для нас выступать вообще как различные аспекты (атрибуты), проявляющиеся в тех или иных условиях эксперимента. Именно в этом случае, для того, чтобы объединить их в актуальное или виртуальное множество, мы даем выражение событийно-структурного взаимодействия. Это по существу и является основанием экспериментального метода в физике элементарных частиц. Эксперимент в физике элементарных частиц есть виртуальное удаленное событие, не принадлежащее актуальной структуре самих частиц, к чему мы еще вернемся при описании имманентной и концептуальной апперцепции.

В этом смысле должны быть описаны множества всех множеств как трансактуальные множества для традиционной теории множеств. Трансактуальные множества есть множества некоторых структурных элементов, поля актуальности которых условно пересекаются в актуальности исследователя, но не в исследуемой области, и которые являются близлежащими лишь концептуально. Трансактуальные множества объединяют элементы разных структур, с разными полями актуальности. Трансактуальное множество имеет вынесенную за пределы элементов актуальность. Их актуальностью является актуальность «наблюдателя», а не их собственная актуальность. В этом смысле множество, представленное Расселом как «множество всех множеств, не содержащих самих себя», есть трансактуальное множество, точно такое же как и трансвиртуальное множество явлений, объединенных в квантовой механике в понятие «частица».

Трансактуальное (трансвиртуальное) множество есть множество релевантных объектов, причем релевантность есть не только актуальная (виртуальная) реферируемость, но и отношение к удаленному событию, то есть затухающая актуальность (виртуальность). Место происхождения этого события не имеет значения для образования трансактуального (трансвиртуального) множества, но имеет значение в дальнейшем для установления референтности между структурой множества и внешней актуальной (виртуальной) структурой события (или событий), объединивших эту структур в множество. Эта затухающая актуальность в физике элементарных частиц преодолевается тем, что наблюдатель вместе с тем, что он навязывает некоторое удаленное событие (эксперимент) некоторым элементам с допустимо разными полями актуальности, навязывает также и свое поле актуальности, в котором действительные поля актуальности некоторых элементов оказываются пересекающимися полями актуальности.

Трансактуальное множество может выступать только как виртуальная реальность, то есть его единство должно задаваться каким-либо событием (в том числе чистым усмотрением). Трансактуальное множество характеризуется исчисляемыми полями актуальности (количество актуальных реальностей, к которым реферирует виртуальная реальность трансактуального множества). Трансактуальное множество характеризуется исчисляемыми объектно-атрибутивными связями. Трансактуальное множество впервые ставит на повестку дня проблему: подлежат ли исчисляемому анализу трансвиртуальные уровни виртуальной реальности, то есть разноуровневые актуальные и виртуальные реальности.

То есть мы ставим главный вопрос исчисления трансактуальных множеств: может ли быть функционально или модельно описано отношение атрибутов объекта виртуальной реальности и аспектов объектов разноуровневых актуальных реальностей, реферирующих с ней. То есть относится ли по какой-либо функции атрибут объекта виртуальной реальности с аспектами в трансактуальной глубине некоторой совокупности объектов актуальной реальности? Иными словами, если одна совокупность объектов установлением объединена в виртуальную реальность, а другая совокупность объектов событийно объединена в актуальную реальность, то есть ли связь между соответствующими их аспектами и атрибутами? Ответ на эти вопросы и есть главная проблема единой теории поля и новых теорий в логике и математике.

Поэтому в связи с этими представлениями Теории Виртуальности требует уточнение и понимание множества. Множество есть актуальное множество — то есть, совокупность реферирующих объектов некоторой актуальной структуры, каждый из которых имеет то же поле актуальности. Там же, где мы рассматриваем свойства, мы всегда должны рассматривать и объект этих свойств или разные объекты этих свойств, а значит речь идет о реальности, которая может быть рассмотрена как трансактуальное множество. Когда мы говорим о виртуальном множестве, то тем самым мы покидаем теорию множеств, и всецело перемещаемся в область Теории Виртуальности.

Изобразим это в виде символизации.

(a, b) — старая запись актуального множества;

[E(a, b)]_i=1{a(e), b(e)} — некий синтез старой и новой записи, где E — событие между объектами a и b, которые объединяют их в множество. В этом синтезе старой и новой записи мы показали, что поскольку интерпретативная референтность равна 1, то раньше левую часть с указанием на событие между объектами отбрасывали, наличие некоторого события E подразумевая. Теперь для нас эта подразумеваемая левая часть становится важной, поскольку эти внешние события могут быть удаленными, а не происходящими между объектами, а референтность между таким трансактуальным множеством и актуальными для него реальностями может быть не только интерпретативная.

Изобразим символически трансактуальное множество, образуемое двумя внешними событиями, относящимися к разным актуальным реальностям.

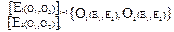
Итак трансактуальное множество состоит из двух объектов O₁ O₂, объединенных в результате двух событий E₁ E₂, одно из которых E₁ относится к его (множества) актуальной структуре (интерпретативная референтность равна 1), а другое событие E₂ удалено, где референтность интерпретативная, но ее значение нельзя точно определить. Обратите внимание, что в трансактуальное множество включены не только объекты O₁ O₂, но им сопоставлены и события (E₁,E₂), которые их объединяют в множество. Данная запись может выражать ситуацию эксперимента для адронов (барионов и мезонов), которые состоят из кварков, то есть событие E₂ относится к уровню адронов, а событие E₁ относится к уровню актуальности экспериментатора. Данная запись также может быть использована, как это мы покажем дальше для понимающей лингвистики компьютерного перевода, где для каждого выражаемого объекта необходимо определять референтность по отношению к шести реальностям, в том числе к реальности самого текста, включая установление каждый раз приблизительной референтности (что и делает человеческое сознание) в случае речевого-языкового взаимодействия в мире объектов.

Для точного различения и операционализации работы с такими множествами мы применяем выписанное нами соотношение «актуальная-виртуальная реальность» с указанием релевантности, вида референтности и исчисление референтности. Эти применения мы выражаем с помощью так называемых ав- ава- и вав-моделей. С помощью этих моделей в ТВ мы рассматриваем: 1) актуальные множества в процессе референтности их элементов в событиях с тождественным полем актуальности (референтность); 2) трансактуальные множества с фиксируемыми (исчисляемыми) полями актуальности (релевантность); 3) разные виды затухающей и направленной релевантной референтности (виды референтности) с искаженным подобием; 4) глубину трансактуального множества (уровень объектно-атрибутивных связей) или поле трансактуальности.

Пока в виде проблемы изложим предположение о реальности как о переплетенных на разных уровнях множествах. Что это за множества и что это за переплетения? Наиболее адекватно эта проблема может быть понята при рассмотрении технологии, которой пользуется сознание для удержания памяти и ее анализа. Эта технология представляет собой переплетение анализа реальности сознанием на уровне множества объектов по их расположению в реальности и на уровне множества объектов для каждого из их свойств. То есть сознание создает связанную цепь трансактуальных множеств, где объединение объектов происходит за счет вынесенной за скобки множества свойства «быть отвлеченным этим сознанием из одной и той же ситуации». Другой способ объединения тех же объектов в множества происходит за счет анализа их содержания и выделение других общих свойств, других атрибутов.

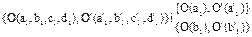
То есть для некоторой ситуации, положения дел или события, память о котором хранится в правом полушарии мозга, создается континуум, для чего сознание отвлекает в левое полушарие два трансактуальных множества {O(a₁), O'(a'₁)} и {O(b₁), O'(b'₁)}. Для любой теории множеств это одно и то же множество {O, O'}. Для ТВ это разные трансактуальные множества, которые могут быть превращены в разные виртуальные реальности для последующего их референтного анализа: [O(a₁,b₁,c₁,d₁)]_iO(a₁), [O'(a₁,b₁,c₁,d₁)]_iO'(a'₁), [O(a₁,b₁,c₁,d₁)]_iO(b₁) и [O'(a'₁,b'₁,c'₁,d'₁)]_iO'(b'₁). Более того каждое из этих трансактуальных множеств имманентно содержит допустимость построения набора выражений об объектах, в них входящих B₁(O), B₁(O') и т.д. То есть тем самым мы указываем на то, что способ оперирования сознанием реальностью и создания множеств является более сложным, чем это рассматривала до сих пор теория множеств. ТВ никак не отменяет теорию множеств, но расширяет инструменты для анализа трансактуальных структур, их релевантно-референтного соотношения, которое в одно и то же время предполагает допустимость построения выражений о каждом из объектов, установления истинности, модальности и т.д.