Основы теории множеств Алгебра множеств.
Алгебра
Алгебра - множество  (несущее множество, носитель алгебры) вместе с заданной на нем совокупностью операций
(несущее множество, носитель алгебры) вместе с заданной на нем совокупностью операций 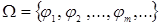 (сигнатурой), т.е. система
(сигнатурой), т.е. система 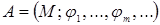 .
.
Алгебра множеств
Непустая совокупность подмножеств некоторого множества  , замкнутая относительно теоретико-множественных операций (объединения, пересечения, разности, дополнения).
, замкнутая относительно теоретико-множественных операций (объединения, пересечения, разности, дополнения).
Бесконечное множество
Множество, которое содержит бесконечное число элементов.
Бинарная операция
Операция, заданная на некотором множестве, называется бинарной, если она действует на два элемента этого множества и её результатом является элемент этого же множества.
Булеан множества
Множество всех подмножеств множества  , обозначаемое Â(А) (или
, обозначаемое Â(А) (или 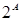 ).
).
(То же, что и множество-степень).
Двойственные соотношения
Соотношения, одно из которых получается заменой в другом следующих символов: 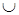 на
на 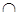 и
и 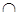 на
на 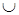 , а также
, а также 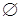 на
на 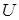 и
и 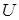 на
на 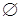 . Соответствующие пары символов
. Соответствующие пары символов 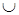 ,
, 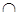 и
и 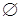 и
и 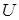 называются двойственными (дуальными) символами.
называются двойственными (дуальными) символами.
Диаграммы Эйлера-Венна
Используются для наглядного представления отношений между подмножествами универсального множества 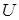 .
.
Дизъюнктивная сумма
Множество, состоящее из всех элементов множества  , не принадлежащих множеству
, не принадлежащих множеству  , и всех элементов множества
, и всех элементов множества  , не принадлежащих множеству
, не принадлежащих множеству  , и не содержащее никаких других элементов.
, и не содержащее никаких других элементов.
(То же, что и симметрическая разность).
Дополнение(теоретико-множественная операция)
Множество 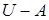 называется дополнениеммножества
называется дополнениеммножества  , т.е. это множество элементов универсума, которые не принадлежат
, т.е. это множество элементов универсума, которые не принадлежат  .
.
(То же, что и отрицание).
Класс
Множество, элементами которого являются множества.
(То же, что и семейство).
Конечное множество
Множество, содержащее конечное число элементов.
Множество
Совокупность объектов произвольной природы, которые удовлетворяют двум свойствам: все объекты этой совокупности попарно различимы; существует некий признак принадлежности объекта этой совокупности.
Множество-степень
То же, что и булеан множества.
Мощность множества
Мощность конечного счётного множества есть число его элементов.
Мультимножество
При многократной записи одного и того же элемента множество называют мультимножеством.
Нестрогое включение
Запись 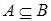 означает, что А - подмножество множества В, возможно, совпадающее с ним.
означает, что А - подмножество множества В, возможно, совпадающее с ним.
Несущее множество (носитель)
Множество  в алгебре
в алгебре 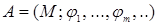 .
.
Нульарные операции
Фиксированные элементы множества  (называются также выделенными элементами, иногда нулями).
(называются также выделенными элементами, иногда нулями).
Объединение(теоретико-множественная операция)
Объединением множеств  и
и  называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств
называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств  или
или  .
.
(То же, что и сумма).
Отрицание(теоретико-множественная операция)
(То же, что и дополнение).
Пересечение
Пересечением множеств  и
и  называется множество, состоящее из всех тех и только тех элементов, которые принадлежат и
называется множество, состоящее из всех тех и только тех элементов, которые принадлежат и  , и
, и  .
.
Подмножество
Множество  , все элементы которого принадлежат и множеству
, все элементы которого принадлежат и множеству  , называется подмножеством множества
, называется подмножеством множества  .
.
Порождающая процедура
Процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определенного множества.
Пустое множество
Множество, не содержащее ни одного элемента (обозначается специальным символом Æ).
Равенство множеств
Неупорядоченные множества равны, если они содержат одинаковый набор элементов.
Разбиение множества
Система множеств, в которой все попарные пересечения множеств пусты, называется разбиением множества 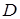 всех элементов этих множеств, а множества такой системы называются классами.
всех элементов этих множеств, а множества такой системы называются классами.
Разность (теоретико-множественная операция)
Разность  и
и  (обозначается
(обозначается 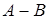 или
или 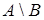 ) - это множество, состоящее из тех и только тех элементов, которые принадлежат
) - это множество, состоящее из тех и только тех элементов, которые принадлежат  и не принадлежат
и не принадлежат  .
.
Семейство
(То же, что и класс).
Сигнатура
Множество операций над элементами множества  , т.е.
, т.е. 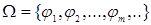 , где
, где 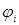 - операции.
- операции.
Симметрическая разность
(То же, что и дизъюнктивная сумма).
Строгое включение
Подмножество А множества В, которое не совпадает с множеством В.
Сумма
(То же, что и объединение).
Счетное множество
Множество А называется счетным, если его объекты можно пересчитывать (каждому объекту множества присвоить натуральное число, которое было бы номером лишь одного элемента множества).
