Основные операции над случайными событиями

Пусть имеется несколько случайных событий. Тогда из них можно строить новые случайные события, используя логические связки «ИЛИ» и «И», которым в теории множеств соответствуют операции объединения и пересечения. В теории вероятностей эти операции называются сложением и умножением, а результаты этих операций – суммой и произведением событий.

Рассмотрим следующий пример. Пусть проводится стрельба двух стрелков (каждый делает по одному выстрелу). Событие А означает, что попал в цель первый стрелок, событие В – попал в цель второй стрелок. Введем в рассмотрение еще два события:

С – попал в цель хотя бы один стрелок;

D – попали в цель оба стрелка.

Нетрудно понять, что событие С наступит тогда, когда произойдет либо одно из событий А или В, либо оба этих события вместе. Событие D произойдет только тогда, когда наступит и событие А и событие В.

Суммойсобытий А и В называется такое событие С=А+В, которое происходит тогда, когда произошло по крайней мере одно из событий А или В.

По определению сумма событий состоит из всех возможных исходов событий А и В, поэтому сумма случайных событий геометрически соответствует объединению множеств, которые определяют события А и В соответственно. Таким образом, для суммы (или объединения) случайных событий А и В имеет место геометрическая интерпретация, где суммой С=А+В является заштрихованная часть плоскости:

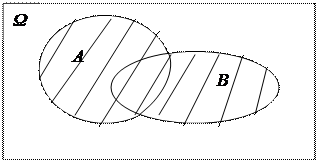Рис.2.7.

Особое значение для решения примеров имеет следующий очевидный факт: Сумма двух противоположных событий для данного испытания является достоверным событием, т.е.

А+Ā = U.

Сумма событий может состоять не из двух, а из большего числа слагаемых. Тогда суммой конечного числа событий А₁, А₂, …, А_n называется событие которое происходит тогда, когда произошло хотя бы одно из событий А₁, А₂, …, А_n.

Произведениемсобытий А и В называется такое событие D = А·В, которое происходит тогда и только тогда, когда произошло и событие А и событие В.

Для совместных событий А и В можно дать следующую геометрическую интерпретацию произведения событий, как пересечения двух множеств, соответствующих событиям А и В:

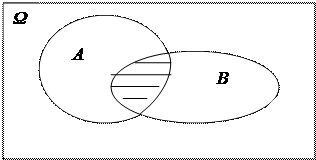Рис.2.8.

Ясно, что для несовместных событий А и В их произведение есть пустое множество.

Произведение противоположных событий также является пустым множеством, т.е.

А·Ā = Λ.

Произведение событий, также как и сумма событий может состоять не из двух, а из конечного числа сомножителей.

Произведением конечного числа случайных событий А₁, А₂, …, А_n называется случайное событие, которое происходит тогда и только тогда, когда произошли все события А₁, А₂, …, А_n.

Для решения задач бывает полезно использовать следующие простые соотношения:

А или В <=> А + В

А и В <=> А · В

Операции сложения и умножения случайных событий обладают следующими свойствами:

1) А + В = В + А – коммутативность сложения;

2) А + (В + С) = (А + В) + С – ассоциативность сложения;

3) А · В = В · А – коммутативность умножения;

4) А · (В · С) = (А · В) · С – ассоциативность умножения;

5) А · (В + С) = А · В + А · С – дистрибутивность.

Используя операции сложения и умножения можно сложные (составные) события разложить на менее сложные или простые события, что будет существенно упрощать решение задачи.

Кроме суммы и произведения существует понятие разности событий.

Разностьюсобытий А и В называется событие А\В, которое происходит тогда, когда произошло событие А и не произошло событие В.