Построение противоположного высказывания

Пользуясь законами де Моргана, нетрудно определить правило, по которому строится высказывание, противоположное данному. Для построения противоположного высказывания, следует записать высказывание в виде формулы, а затем надчеркнуть эту формулу и упростить полученное высказывание, пользуясь доказанными законами математической логики.

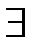Очень часто в высказываниях (особенно, математических) присутствуют кванторы общности ( ) или существования ( ). При построении противоположного высказывания данные кванторы взаимно заменяют друг друга. Поэтому правило построения высказывания, противоположного высказыванию, содержащему кванторы, такое. В исходном высказывании выделяется основная фраза, которая содержится в последней части высказывания. При построении противоположного высказывания кванторы взаимно заменяются, а последняя фраза заменяется на противоположную.

Примеры.1. Исходная фраза: «Каждого человека посещает мысль о том, что либо он должен поместить все деньги в банк, либо приобрести акции нефтяных компаний».

Запишем с помощью кванторов: « у человека 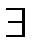мысль (( деньги положить в банк) (приобрести акции нефтяных компаний))». То, что мы поместили в скобку, и есть основная фраза, содержащаяся в последней части высказывания. Фраза, противоположная той, что в скобках, в формальной записи имеет вид: (( 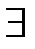деньги, не положенные в банк) (не приобретать акции нефтяных компаний)). Операция дизъюнкции заменена на операцию конъюнкции в соответствии с законом де Моргана. 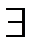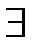Запись высказывания, противоположного исходному, в кванторах имеет вид: « человек , у которого мысль (( деньги, не положенные в банк) (не приобретать акции нефтяных компаний))».

После некоторой литературной обработки наше высказывание принимает вид: «Есть люди, твердо уверенные в том, что не все деньги следует доверять банкам и что нельзя покупать акции нефтяных компаний».

2. Аналогичным способом строятся высказывания, противоположные математическим, таким как «Для любого 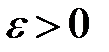существует 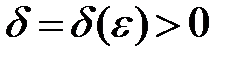такое, что при любом 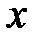, обладающем свойством 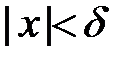, выполняется неравенство ».

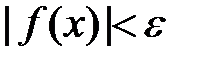Запишем исходное высказывание в кванторах: « 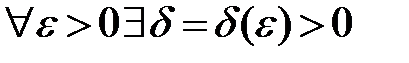такое, что 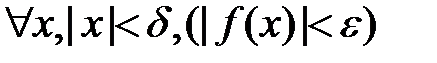». Противоположное высказывание в кванторах имеет вид « 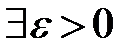такое, что 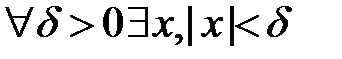,( 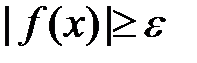)». Читается противоположное высказывание так: «существует такое 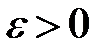, что для любого положительного 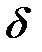можно подобрать такое 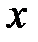, что 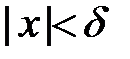, и при этом ».

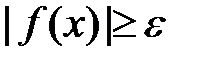Кстати, исходное высказывание – это математическое определение того факта, что функция 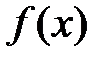имеет в точке 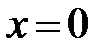предел, равный 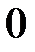. Противоположное высказывание – это математическое определение того, что у функции 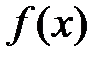в точке 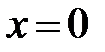либо не существует предела, либо есть предел, отличный от нуля.

Задания

1. Среди предложений выделите высказывания и определите их истинностные значения: 1) Рыбы живут в воде. 2) Осень – хорошее время года. 3) Казань – столица США. 4) Волга впадает в Каспийское море. 5) Не ходи сюда! 6) 2 + 2 = 4. 7) 3 – 5 = 8.

2. Пусть А: «Сегодня буду писать отчет»; В: «Сегодня буду отдыхать»; С: «На улице идет дождь». Сформулируйте предложения соответствующие формулам:

1) А^В, 2) С^В, 3) ⌐А^В, 4) С^А, 5) А Ú ⌐В, 6) ⌐ С Ú А, 7) С→ ВÚА, 8) (В↔С) ^А.

3. Составьте формулы, соответствующие повествовательным предложениям, обозначая буквами элементарные высказывания: 1) Идет дождь или кто-то не выключил душ; 2) Если вечером будет туман, то я останусь дома или вынужден буду взять такси; 3) Если я устал или голоден, то не могу заниматься; 4) Если Роман проснется и пойдет на лекцию, то он будет доволен, а если не проснется, то не будет доволен; 5) Хлеба уцелеют тогда и только тогда, когда будут вырыты ирригационные канавы, а если хлеба не уцелеют, то фермеры обанкротятся и оставят свои фермы.

4. Сформулируйте словесно высказывания:

1) (АÚ В) →С, С→(А^В), где А: лето жаркое; В: лето дождливое; С: я поеду в отпуск;

2) (А^ В) →С, (АÚ В) → С, где А: фигура ромб; В: фигура прямоугольник; С: фигура параллелограмм;

3) (⌐ АÚВ) → ⌐С, С→(АÚ ⌐В), где А: сегодня светит солнце; В: сегодня сыро; С: я поеду на дачу.

5.Докажите с помощью таблиц истинности равносильность формул:

1) А → (В → С) º (А^В) →С;

2) ( А→В) ^(А→С) º А→(В^С).

6.В результате тестирования были установлены следующие факты(И):

1) если Иванов не увлекается историей, то либо Петров , либо Сидоров ею увлечены, причем не Сидоров и Иванов одновременно;

2) если Сидоров не увлечен историей, то Иванов увлечен ею, Петров нет;

3) если Иванов историк, то и Сидоров историк.

Выяснить, кто согласно указанным фактам увлекается историей.

7.Пусть значение высказывания А →В = И, что можно сказать о значении высказывания

⌐А ^В ↔А ÚВ?

8. Проверить, является ли данная логическая формула тавтологией:

1) (А Ú В) → В Ú⌐А; 2) А Ú В ↔⌐(⌐А ^ ⌐В); 3) А → (А Ú (⌐В^ А)).

9. Переведите каждое рассуждение в логическую символику и установите, имеет ли место в нем логическое следование:

1) Если он принадлежит к нашей компании (К), то он храбр (Х) и на него можно положиться (П). Он не принадлежит нашей компании. Значит, он не храбр или же на него нельзя положиться.

2) В бюджете возникнет дефицит (D), если не повысят пошлины (P). Если в бюджете имеется дефицит, то государственные расходы на общественные нужды сократятся (O). Значит, если повысят пошлины, то государственные расходы на общественные нужды не сократятся.

3) Если он автор этого слуха (А), то он глуп (Г) или беспринципен (Б). Он не глуп и не лишен принципов. Значит, не он автор этого слуха.

4) Если бы он ей не сказал, она ни за что не узнала бы. А не спроси она его, он бы и не сказал. Но она узнала. Значит: Она его спросила.

5).Если бы он не пошел в кино, он не получил бы двойки. Если бы он подготовил домашнее задание, то он не пошел бы в кино. Он получил двойку. Значит, он не подготовил домашнее задание.

10.Проверить правильность рассуждения средствами логики суждений: «Если бы он не пошел в кино, он не получил бы двойки. Если бы он подготовил домашнее задание, то он не пошел бы в кино. Он получил двойку. Значит, он не подготовил домашнее задание».

19. Пользуясь правилом построения противоположного высказывания, записать утверждения, противоположные следующим:

1) На любом курсе каждого факультета КГУ есть студенты, сдающие все экзамены на «отлично».

2) Каждый студент философского факультета КГУ имеет друга, который умеет решать все логические задачи.

3) В любом самолете на рейсе Вашингтон-Москва присутствует хотя бы один сотрудник силовых органов, в каждой пуговице одежды которого вмонтирован микрофон.

Элементы теории множеств

Понятие множестваили совокупности принадлежит к числу простейших математических понятий. Оно не имеет точного определения. Любое множество задается своими элементами. Примерами являются множество книг в библиотеке или множество студентов, присутствующих на занятии. Обычно множество обозначают заглавными латинскими буквами (A), а его элементы строчными латинскими буквами (a). То, что элемент принадлежит множеству, обозначают так: a 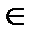A. Если a не принадлежит A, то этот факт обозначают так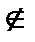: a A.

Чтобы задать множество, следует или перечислить его элементы, или указать характеристическое свойство его элементов, то есть такое свойство, которым обладают все элементы множества и только они.

Примеры. 1. Множество натуральных чисел можно задать так: N={1, 2, 3,…,n, n+1,…}. Из записи следует, что все натуральные числа, начиная с двойки, получаются прибавлением единицы к предыдущему числу.

2. Множество целых чисел можно задать так: Z={0, 1 ,–1, 2, –2,…,n, –n,…}.

3. Множество рациональных чисел можно задать так:

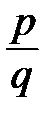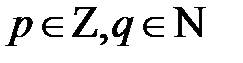={ | }. Вертикальная черта внутри фигурной скобки

означает, что далее идет описание характеристических свойств введенных обозначений.

Два множества равны тогда и только тогда, когда состоят из одних и тех же элементов. Если все элементы множества A содержатся в множестве B, то говорят, что A является подмножеством множества B и обозначают A 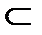B.

В рамках рассматриваемой математической теории вводят два исключительных множества: пустое множество ( 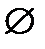), не содержащее элементов, и универсальное множество или «универсум» (U), содержащее все элементы данной теории.

Аксиоматика операций над множествами

Основными операциями над множествами являются следующие.

1. Дополнение.Для любого множества 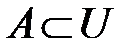определим дополнение .

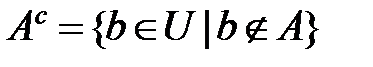Например, в множестве вещественных чисел дополнением к множеству 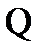является множество всех иррациональных чисел.

2. Объединение.Для любых двух множеств 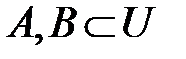определим объединение .

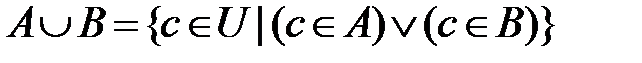Например, объединением отрезков [1,3] и [2,7] является отрезок [1,7].

2. Пересечение.Для любых двух множеств 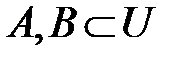определим пересечение .

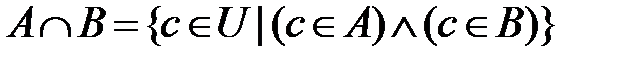Например, пересечением отрезков [1,3] и [2,7] является отрезок [2,3].

Для иллюстрации операций над множествами вводят диаграммы Эйлера-Венна – круги, обозначающие множества. Так, введенные нами операции иллюстрируются следующим образом.

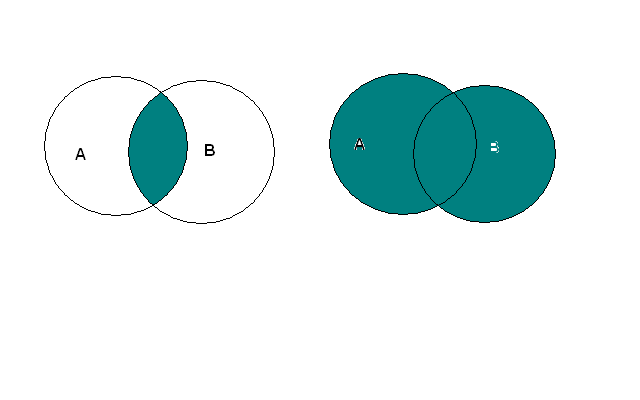
А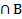

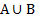
Подчеркнем, что диаграммы Эйлера-Венна не могут служить доказательствами равенства множеств.

Кроме введенных нами трех операций над множествами существуют еще операции, которые могут быть представлены как комбинация простейших операций. Введем операцию вычитаниямножеств:

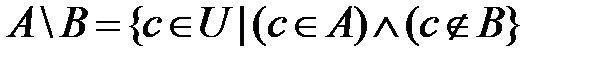. На диаграмме Эйлера-Венна результат вычитания выглядит так: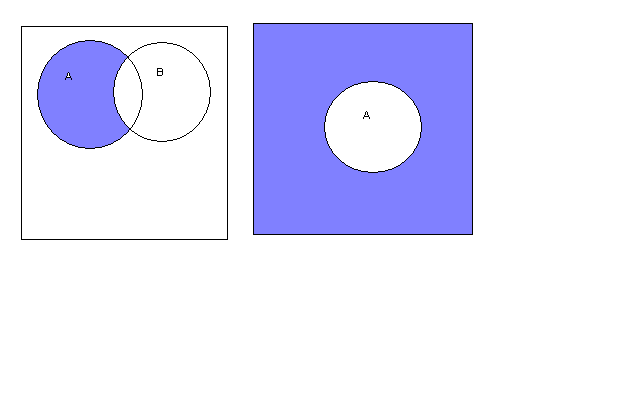

А\В 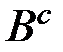= U\В

Докажем, что 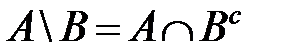. Для доказательства равенства двух множеств следует убедиться в том, что все элементы первого множества принадлежат второму и все элементы второго множества принадлежат первому.

а) Пусть 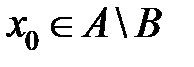. Из определения следует, что справедливо высказывание 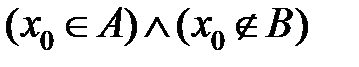. Из определения дополнения к множеству 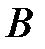следует, что 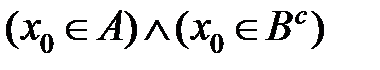. Теперь из определения пересечения множеств следует, что 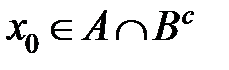. То есть, любой элемент из множества 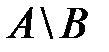принадлежит множеству .

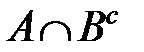б) Пусть 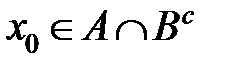. Из определения пересечения множеств следует, что 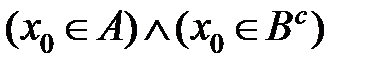. Из определения дополнения множества получим 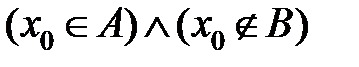. В соответствии с определением разности множеств 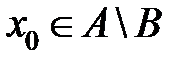. Следовательно, любой элемент из множества 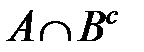принадлежит множеству .

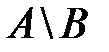Доказательство равенства двух множеств закончено.

Нетрудно заметить, что при доказательстве, связанном с множествами, большую роль играют высказывания, присутствующие в определении высказывания. Поскольку эти высказывания содержат логические операции, естественно предположить, что законы, справедливые для логических операций, могут быть перенесены на множества. Это, действительно, так.