Высказывания и логические операции над ними
2. Формулы логики высказываний и их классификация
3. Общезначимые формулы
4. Логическое следование
5. Равносильность формул
6. Нормальные формы для формул алгебры высказываний
Формализованное исчисление высказываний
Теорема о дедукции
Полнота, непротиворечивость и разрешимость исчисления высказываний
10. Предикаты и их классификация.
11. Логические и кванторные операции над предикатами
Формулы логики предикатов и их классификация
Равносильность и логическое следование формул логики предикатов
Формализованное исчисление предикатов
15. Классическая логика и клаузальная логика
Логическое программирование. Клаузы Хорна и метод резолюций
Модальная логика
18. Нечеткая логика
19. Темпоральная логика
20. Задачи и алгоритмы. Свойства алгоритма.
21. Машина Тьюринга
22. Рекурсивные функции
23. Нормальные алгоритмы Маркова
24. Алгоритмически неразрешимые проблемы
Образец контрольной работы
1. Докажите, что теория графов в сигнатуре без равенства неполна.
2. Может ли полная теория в сигнатуре с равенством иметь нормальную конечную модель и нормальную бесконечную модель?
3. Пусть Т – полная теория с равенством, имеющая конечную модель. Докажите, что Т не имеет бесконечных моделей.
4. Докажите, что не существует теории первого порядка в сигнатуре {+,,=,0,1}, моделями которой являются в точности все конечные поля. Аналогично -- для полей ненулевой характеристики.
5. Переведите в логическую символику и проверьте общезначимость полученной формулы:
В пьесе у каждого участника есть брат и сестра, также участвующие в этой пьесе. Никто не является своим собственным братом или сестрой. Брат не может быть сестрой. Значит, либо в этой пьесе нет вовсе действующих лиц, либо же их не меньше четырех.
6. Постройте формулу 1-го порядка без равенства, имеющую 3-элементную модель, но не имеющую 2-элементных моделей.
Образец заданий для типового расчёта
ТР №1
1. Записать булевы выражения А, В и С в стандартных обозначениях
2. Проверить, эквивалентны ли А и В
3. Привести В и С к КНФ и ДНФ
4. Написать двойственное к С выражение в виде многочлена Жегалкина
5. Указать, при каких значениях переменных В истинно
6. Проверить А на линейность и монотонность
7. Проверить, не являются ли А, В и С тавтологиями
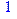
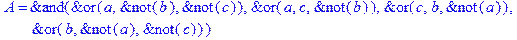
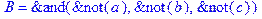

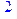
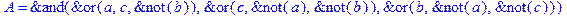
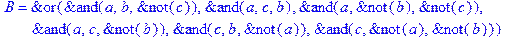
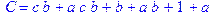
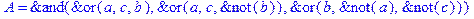
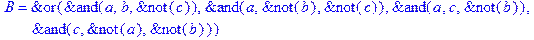
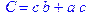
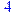
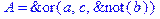
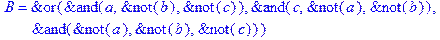
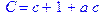
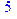
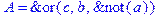
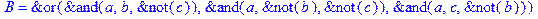
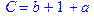
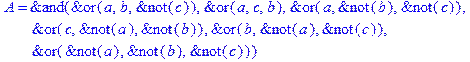
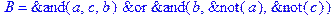
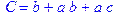
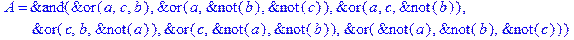
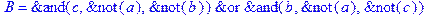
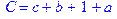
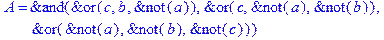

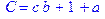
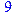
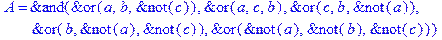
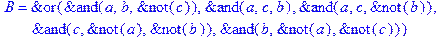
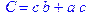
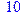
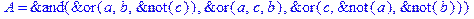

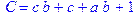
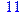
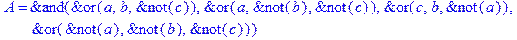
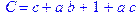
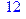
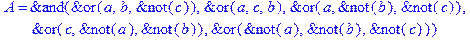


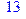
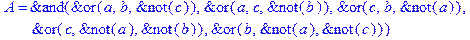
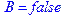
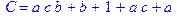
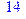
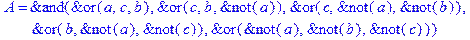
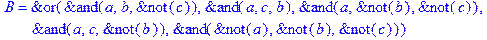
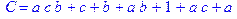
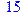
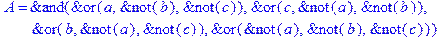
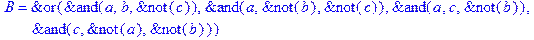
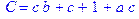
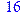
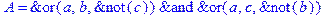
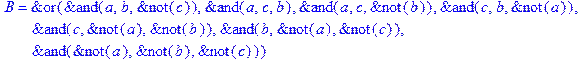
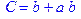
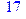
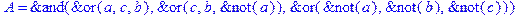
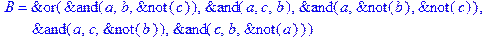
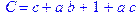

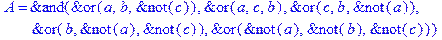
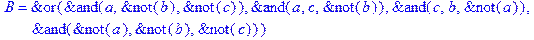
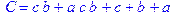
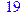
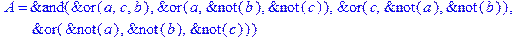
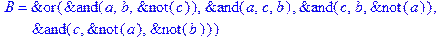
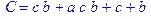
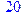
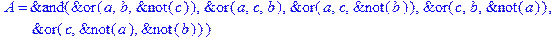
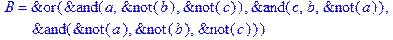
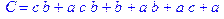
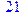
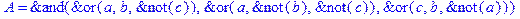
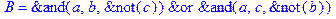
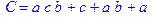
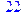
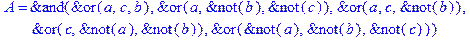
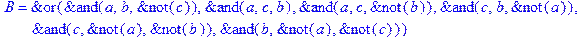
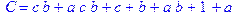
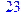


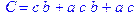
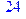
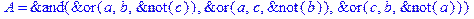
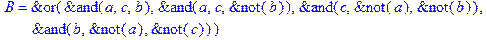
ТР №3
1. Нарисовать контактно-релейные схемы, соответствующие A,B,C
2. Упростить А и изобразить соответствующую упрощенную схему
3. Нарисовать схему для С, использующую только элементы "и-не"
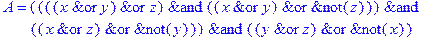
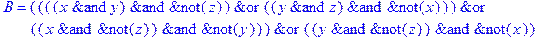
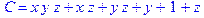
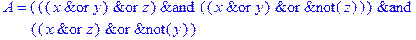
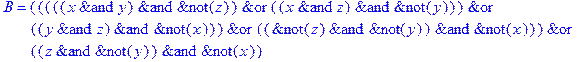
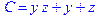

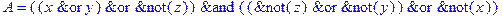
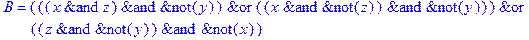
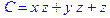
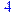
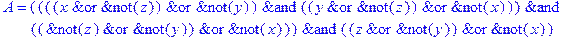
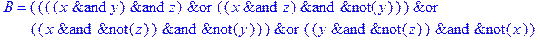
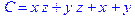
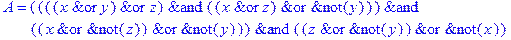
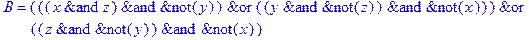
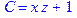
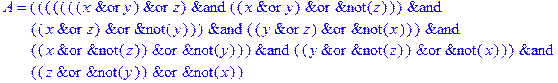
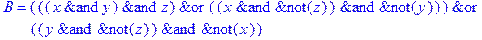
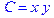
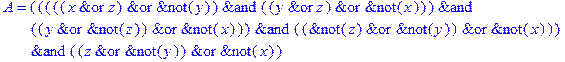
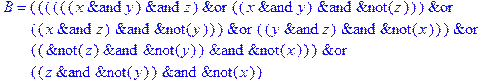
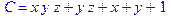
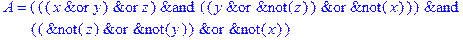
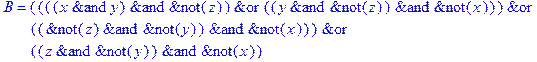
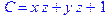
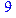
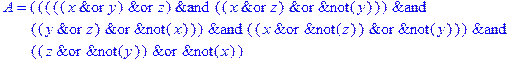
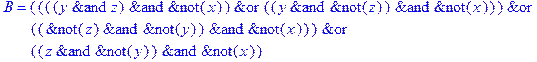
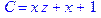
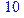
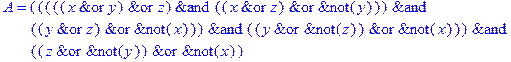
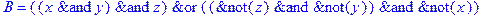
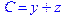
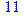
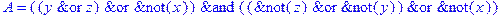
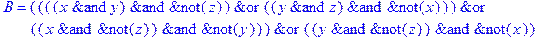
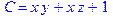
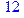
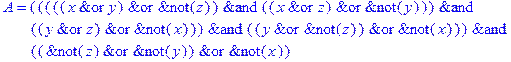
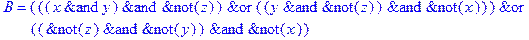
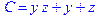
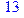
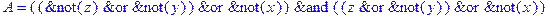
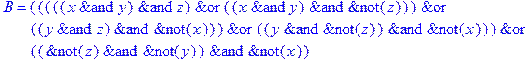
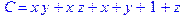
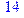
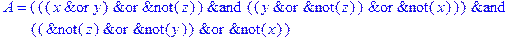
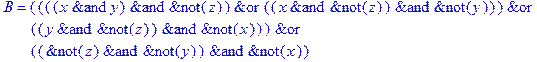
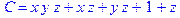
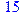
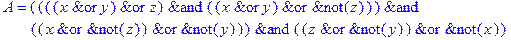
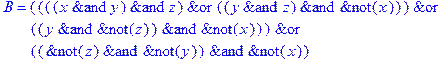
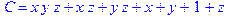
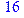
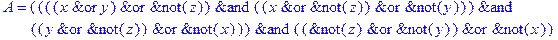
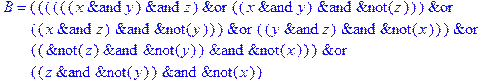
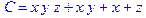
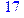
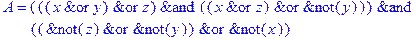
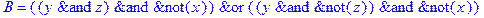
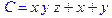
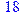
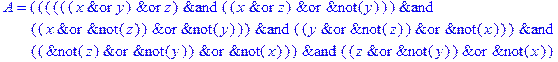
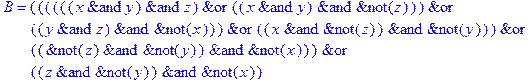
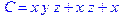
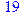
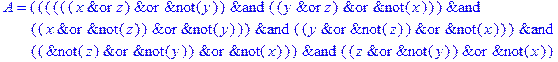
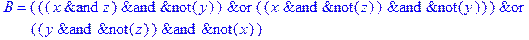
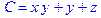
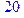
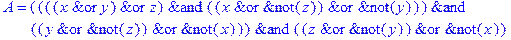
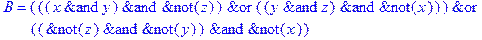
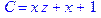
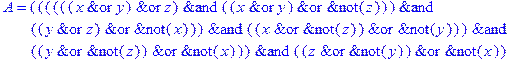
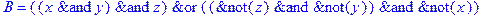
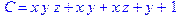
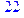

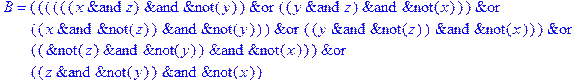
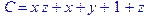
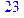
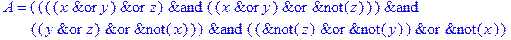
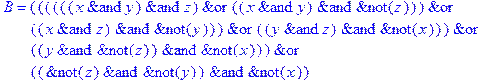

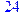
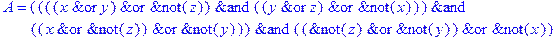
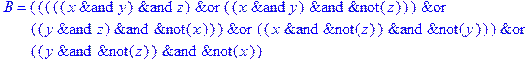
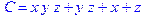
Примеры вариантов тестовых заданий
Вариант 1.
1. Какое из следующих равенств с множествами А и В является ложным:
1) 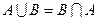 ; 2)(А
; 2)(А 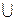 В)
В) 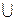 С=А
С=А 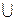 (В
(В 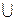 С); 3) Если
С); 3) Если 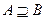 , то А
, то А 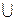 В= А; 4)А
В= А; 4)А 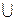 Ø= А.
Ø= А.
2. Дизъюнкцией высказываний А и В (обозначение АÚВ, читается: А или В) называется высказывание:
1) истинное тогда, когда истинно хотя бы одно из высказываний А и В, и ложное, если и А и В ложны
2) ложное в случае, если А истинно, а В ложно, и истинное в остальных случаях
3) истинное тогда, когда истинны оба высказывания А и В, и ложное в остальных случаях
4) истинное тогда, когда оба высказывания А и В либо истинны, либо ложны, и ложное если одно из высказываний А, В истинно, а другое ложно
3. Квантор общности обозначается символом:
1); 2)^; 3) 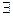 ; 4)
; 4) 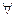
4. Информационная ленты, считывающая и записывающая головка и управляющее устройство – это состав машины:
1)Черча; 2)Маркова; 3)Паскаля; 4)Тьюринга
5. Оператор минимизации обозначается:
1) Jn,m ; 2) l (x);3) my; 4)R(g(n) ; h(n+2))
21.Пусть g(х)=Ci(х)=0; h(х;у;f (х; у)) = J3,2=y. Пользуясь схемой примитивной рекурсии найти f(3):
1)0; 2)1; 3)2; 4)5
Вариант 2.
1. Какое из следующих равенств с множествами А и В является ложным:
1) 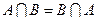 ; 2)(А
; 2)(А 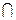 В)
В) 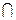 С=А
С=А 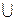 (В
(В 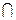 С);3)Если
С);3)Если 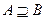 , то А
, то А 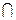 В= В; 4)А
В= В; 4)А 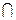 Ø=Ø;
Ø=Ø;
2. Формула 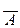 V
V 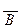 »
» 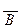 V
V 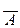 представляет собойзакон:
представляет собойзакон:
1)идемпотентности 3)ассоциативности
2)коммутативности 4)тавтологии
3. Неразрешимость проблемы разрешения для множества всех истинных предложений логики предикатов установил:
1)Черч;2) Марков; 3) Паскаль; 4) Тьюринг
4. Функция следования обозначается:
1) Jn,m ; 2) l (x);3)my; 4)R(g(n) ; h(n+2))
5. Пусть g(x)=J1,1=x; h (х; у; f (х; у)) = l (J3,3) = f (x; у) + 1
Пользуясь схемой примитивной рекурсии найти f(3;6):
1)3; 2)6; 3)9; 4)12
Вариант 3.
1 . Какое из следующих равенств с множествами А и В является ложным:
1) 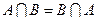 ; 2) (А
; 2) (А 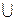 В)
В) 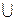 С=А
С=А 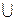 (В
(В 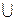 С); 3) Если
С); 3) Если 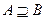 , то А
, то А 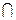 В= А;4)А
В= А;4)А 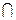 Ø=Ø
Ø=Ø
2. Какое из следующих свойств логических операций является неверным:
1) (ù ù ùА) Û (А); 2)( ù (АÚВ)) Û (ùАÙùВ); 3)( ù (АÙВ)) Û (ùАÚùВ); 4) ((АÚВ)ÚС) Û (АÚ(ВÚС))
3. К числу элементарных операций не относят операцию:
1)константы;2)суперпозиции; 3)рекурсии; 4)минимизации
4. Пусть g(x) = I1,1 = x; h (х; у; f (х; у)) = l-1 (J3,3) = f (x; у) – 1
Пользуясь схемой примитивной рекурсии найти f(6;3):
1)3; 2)6; 3)9; 4)12
Критерии оценивания
Решения типовых расчётов и домашних заданий представляются в любой читаемой форме (в бумажном или электронном виде – по выбору студента).
Каждая правильно решенная задача оценивается в зависимости от её трудности и объёма вычислений.
Контрольные работы зачитываются при решении не менее 60% задач, а типовые расчёты – не менее 80% задач. В противном случае, оценка за работу в целом – нулевая.
Приложение 5
к рабочей программе дисциплины
«Математическая логика и теория алгоритмов»
Таблица планирования результатов обучения студентов 1 курса по дисциплине«Математическая логика и теория алгоритмов»во 2 семестре
| Модуль 3 | Модуль 4 | |||||||||||||||||||
| Текущий контроль по точкам | Рубежный контроль | Текущий контроль по точкам | Рубежный контроль | |||||||||||||||||
| [min] | max | [min] | max | [min] | max | [min] | max | [min] | max | [min] | max | [min] | max | [min] | max | [min] | max | [min] | max | |
| Текущее тестирование | ||||||||||||||||||||
| Допуск к л.р. | ||||||||||||||||||||
| Выполнение л.р. | ||||||||||||||||||||
| Защита отчета по л.р. | ||||||||||||||||||||
| Посещение практических занятий (семинаров) | ||||||||||||||||||||
| Работа на практических занятиях | ||||||||||||||||||||
| Выполнение контрольных работ | ||||||||||||||||||||
| Выполнение домашних заданий | ||||||||||||||||||||
| Работа над рефератом (по этапам) | ||||||||||||||||||||
| Рубежное тестирование | ||||||||||||||||||||
| Личностные качества | ||||||||||||||||||||
| Балловая стоимость одной точки | ||||||||||||||||||||
| Накопление баллов | ||||||||||||||||||||
| Итого: |
Преподаватели: __________________________
Зав. кафедрой: ___________________________
Декан факультета: ________________________
