Способы задания фукции алгебры логики
СБОРНИК ЗАДАЧ ПО АЛГЕБРЕ ЛОГИКИ
УЧЕБНОЕ ПОСОБИЕ
К практическим занятиям
по курсу «Теория дискретных устройств»
(рукопись)
Красноярск 2014
УДК 62.50
Туйгунова А.Г., Худоногов И.А.Сборник задач по алгебре логики: Учебное пособие к практическим занятиям по курсу «Теория дискретных устройств». – Красноярск: КрИЖТ ИрГУПС, 2014. – 49 с.
Учебное пособие к практическим занятиям по курсу «Теория дискретных устройств» содержит задачи анализа и синтеза соответствующих функций алгебры логики. Предназначено студентам, изучающим элементы теории дискретных устройств железнодорожной автоматики, телемеханики и связи, используемые при построении систем телемеханики, при проведении практических занятий и для самостоятельной работы.
Ил. 26. Табл. 16. Библиогр. 8 назв.
Авторы: А.Г. Туйгунова, канд. техн. наук, доцент кафедры «Транспортные системы» КрИЖТ ИрГУПС;
И.А. Худоногов, д-р техн. наук, профессор кафедры «Электроснабжение железнодорожного транспорта» ИрГУПС
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ..................................................................................................................... 4
1. СПОСОБЫ ЗАДАНИЯ ФУКЦИИ АЛГЕБРЫ ЛОГИКИ................................. 5
2. МИНИМИЗАЦИя ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ....................................... 12
3. Преобразование логических функций........................................ 26
4. ПРЕДСТАВЛЕНИЕ ФАЛ В РАЗЛИЧНЫХ БАЗИСАХ................................. 27
5. Реализация ФАЛ на контактных и бесконтактных элементах 28
6. СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ........................................................ 35
6.1. Синтез комбинационных схем с несколькими выходами........................ 35
6.2. Синтез специальных комбинационных схем............................................ 40
Задания для самостоятельной работы................................................ 44
БИБЛИОГРАФИЧЕСКИЙ СПИСОК........................................................................ 49
Введение
Сборник задач рассматривается как учебное пособие для упражнений и практических знаний по разделу «Теория дискретных устройств» соответствующей программы учебной дисциплины.
Сборник задач состоит из семи разделов. Первый раздел позволяет закрепить знания по способам задания и основным законам функций алгебры логики (ФАЛ). Задачи минимизации полностью определенных логических выражений ФАЛ приведены во втором разделе. Третий раздел посвящен преобразованию и упрощению булевых выражений. В четвертом разделе показано представление ФАЛ в различных базисах. Способ реализации ФАЛ на релейно-контактных схемах приведен в пятом разделе. В шестом разделе показан синтез комбинационных схем с несколькими выходами. В седьмом разделе приведены примеры для самостоятельного углубления знаний студентами в теории булевых функций. Решение задач позволит студенту освоить методику формализации содержательной постановки задачи в виде булевого уравнения, логической диаграммы или релейно-контактной схемы и овладеть приемами решения задач.
СПОСОБЫ ЗАДАНИЯ ФУКЦИИ АЛГЕБРЫ ЛОГИКИ
Методы анализа и синтеза всех классов дискретных автоматов строят на базе алгебры логики. Алгебра логики - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Начало алгебры логики было положено ирландским математиком Д.Булем (1815-1864).
Функцию f (х1, х2, ..., хп) называют функцией алгебры логики (ФАЛ), если она, как и ее переменные (аргументы), может принимать только два значения: логического 0 и логической 1. Переменные ФАЛ сопоставляют со значениями сигналов на входах дискретного автомата, а значения функции алгебры логики - со значениями сигналов на его выходах.
Реальные дискретные автоматы имеют конечное число входов, следовательно, число переменных у соответствующих ФАЛ также конечно. Так как переменные ФАЛ могут принимать только два значения, область определения любой ФАЛ конечна.
Базисом называют полную систему функций алгебры логики. Минимальный базис состоит из такого набора функций, исключение из которого любой функции превращает этот набор в неполную систему функций. Наиболее удобным для представления в виде логического выражения функций алгебры логики является базис, содержащий конъюнкцию, дизъюнкцию и инверсию (И, ИЛИ, НЕ). Этот базис называют основным. Минимальный базис включает в себя две функции: И, НЕ или ИЛИ, НЕ, однако использование трех функций упрощает логическое описание, а в ряде случаев и построение дискретных устройств железнодорожной автоматики, телемеханики и связи.
Для начального представления функций обычно применяют основной базис И, ИЛИ, НЕ независимо от того, какой базис будет использован для построения дискретного устройства.
Решение вопросов анализа и синтеза схем дискретных устройств железнодорожной автоматики, телемеханики и связи связано с преобразованием выражений, которые содержат ФАЛ основного базиса. Запись, содержащая двоичные переменные, соединенные знаками логического сложения, умножения и инверсии, называют логическим выражением. Такое выражение однозначно определяет комбинационное устройство, построенное на элементах И, ИЛИ, НЕ.
При табличном способе ФАЛ задают таблицей ее значений в зависимости от значений переменных. Таблицу, в которой для всех наборов переменных приводятся значения ФАЛ, называют таблицей истинности. Например, в таблице 1 заданы две ФАЛ трех переменных: f (x1, х2, ..., хn) и φ (х1, x2, ..., хn).
Таблица 1
| Номер | x1 | х2 | х 3 | f | φ |
Совокупность значений переменных называют набором (точкой). Каждому набору переменных соответствует определенное значение функции. Если ФАЛ содержит п переменных, двоичные числа будут разрядные и, следовательно, общее число наборов определяется по формуле k = 2п. При трех аргументах можно образовать восемь наборов. Следовательно, приведенные в табл. 1 функции f (x1, х2, ..., хп) и φ (х1, x2, ..., хп) определены на восьми наборах. При этом каждый набор представляет собой трехразрядное двоичное число.
При каждом наборе переменных возможны два значения ФАЛ: логического 0 или 1. Поэтому в соответствие каждой ФАЛ можно поставить k-разрядное двоичное число. Значит, число функций алгебры логики п аргументов определяется формулой 2k. При п переменных таблица содержит 2п строк (по числу наборов), п столбцов (по числу переменных) и один столбец значений функции, соответствующих каждому набору (сочетанию) аргументов.
При графическом способе наборам значений переменных ФАЛ сопоставляются точки п-мерного пространства. Множество 2п наборов определяет множество вершин п-мерного единичного куба. Вершинам куба соответствуют наборы значений переменных и приписаны значения функции на этих наборах, т.е. областью определения ФАЛ, зависящей от п переменных, является множество вершин единичного п-мерного куба. Куб называют единичным, так как каждое его ребро соединяет вершины, наборы которых различаются одной переменной. Функции f (x1, х2, ..., хп) и φ (х1, x2, ..., хп) - заданные таблицей истинности (см. табл. 1), можно задать графически (рис. 1).
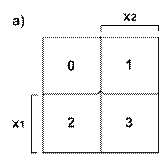
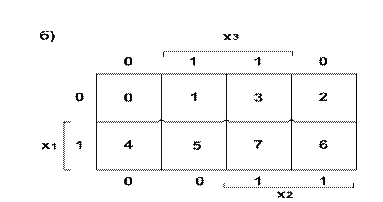
При координатном способе функцию задают в виде координатной карты состояний, которую называют картой Карно. Карты представляют собой прямоугольные таблицы, разделенные горизонтальными и вертикальными линиями на клетки. Общее число клеток соответствует числу наборов функции. Все переменные функции разбивают на две группы, Одна группа переменных определяет выбор строки, другая - столбца. На пересечении строки и столбца находится клетка, в которую записывают значение функции при соответствующем наборе переменных. Аргументы разделяются на группы так, чтобы в соседних клетках наборы различались только значением одной переменной. Карты Карно для двух, трех и четырех и пяти переменных приведены соответственно на рис. 2,а, б, в, г. В каждую из клеток карты Карно трех переменных вписаны значения функции f (x1, х2, ..., хп) заданной таблицей истинности (см. табл. 1). На рис. 3 в скобках в каждой из клеток карты Карно проставлены десятичные номера соответствующих наборов.
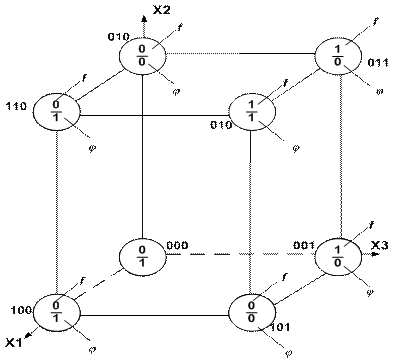
Рисунок 1 - Графическое задание ФАЛ
При числовом способе каждому набору переменных ставят в соответствие определенное число в двоичной системе исчисления и присваивают соответствующий номер. Переменным x1, х2, ..., хп приписывают соответственно веса 2 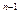 ,2
,2 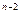 ,…,2
,…,2 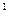 ,2
,2 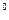 . Функцию задают в виде десятичных номеров тех наборов переменных, на которых она принимает значение 1. Поскольку номер внутреннего состояния зависит от присвоенных переменным весов условимся записывать эти переменные в порядке уменьшения весов. Такую запись называют базой системы нумерации. Так, например, если имеются три переменные x1, х2, х3, причем переменной x1 присвоен вес 22, переменной х2 – 21, а переменной х3 - 20, то база системы нумерации будет x1, х2, х3.
. Функцию задают в виде десятичных номеров тех наборов переменных, на которых она принимает значение 1. Поскольку номер внутреннего состояния зависит от присвоенных переменным весов условимся записывать эти переменные в порядке уменьшения весов. Такую запись называют базой системы нумерации. Так, например, если имеются три переменные x1, х2, х3, причем переменной x1 присвоен вес 22, переменной х2 – 21, а переменной х3 - 20, то база системы нумерации будет x1, х2, х3.
В тех случаях, когда при некоторых наборах аргументов значения функции «безразличны» (не определены), при задании ФАЛ табличным, координатным и графическим способами на таком наборе проставляются знаки «~» или «Ø» (рис. 4).
 |  | |
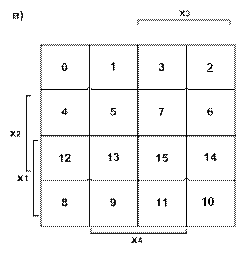 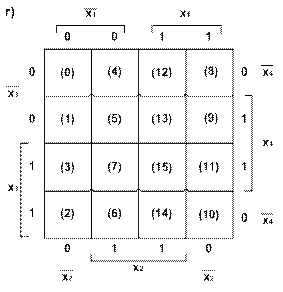 | ||
Рисунок 2 - Координатный способ задания ФАЛ: а) для двух аргументов; б) для трех аргументов; в, г) для четырех аргументов 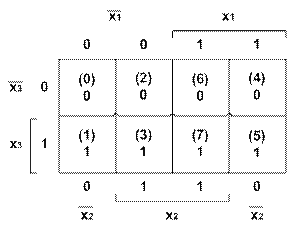 | ||
Рисунок 3 - Задание ФАЛ трех переменных координатным способом
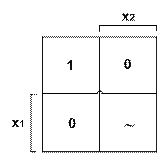
Рисунок 4 - Табличное задание не полностью определенной функции
При числовом способе задания не полностью определенной функции указываются множества наборов, при которых ФАЛ принимает значения 1 (обязательные номера), и наборов, при которых функция равна 0 (запрещенные номера) или ее значения безразличны (условные номера):

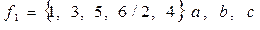 .
.
или
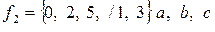
Функции f (x1, х2, ..., хп) и φ (х1, x2, ..., хп), приведенные в табл.1, могут быть заданы числовым способом:
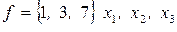 ;
; 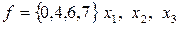 .
.
При аналитическом способе функцию задают в виде алгебраического выражения с указанием логических операции над аргументами функции. В таблице 2 приведен перечень логических операций, используемых при записи логических выражений.
Таблица 2 - Перечень логических операций, используемых при записи логических выражений
| Обозначение логических операций | Таблица истинности | Как читается | Название операции | |||||
| Х1 | ||||||||
| Х2 | ||||||||
| Х1 Х2 Х1 ۸ Х2 Х1 & Х2 | Х1 и Х2 | Конъюнкция; логическое И ; логическое произведение | ||||||
| Х1 ۷ Х2 Х1 + Х2 | Х1 или Х2 | Дизъюнкция; логическое ИЛИ; логическая сумма | ||||||
Х1 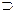 Х2 Х2 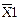 + Х2 Х1→ Х2 + Х2 Х1→ Х2 | Если Х1, то Х2; Х1 влечет Х2; Х1 имплицирует Х2 | Импликация | ||||||
| Х1~Х2 Х1≡Х2 Х1↔Х2 | Х1 эквивалентно Х2 | Эквивалентность; функция равнозначности | ||||||
Х1  Х2 Х2 | или Х1 или Х2; Х1 неэквивалентно Х2 | Функция неэквивалентности; функция неравнозначности; исключающее ИЛИ; сумма по модулю 2 | ||||||
Х1∆Х2 Х1 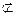 Х2 Х1→Х2 Х2 Х1→Х2 | Х1 запрет по Х2; Х1, но не Х2 | Запрет; отрицание импликации | ||||||
| Х1│ Х2 | Х1 и Х2 не совместны | Штрих-Шеффера; логическое И-НЕ; отрицание конъюнкции | ||||||
| Х1↓ Х2 | не Х1 не Х2 | Стрелка Пирса; логическое И-НЕ; отрицание дизъюнкции | ||||||
 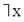 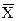 | Х | не Х | Инверсия; логическое отрицание; логическое НЕ | |||||
| У | ||||||||
Алгебраическое выражение может быть составлено из наборов аргументов, на которых функция принимает значение 1, или из наборов аргументов, на которых она принимает значение 0.
Например, можно записать ФАЛ трех аргументов в виде:
f = ( 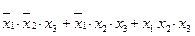 )
)
ИЛИ
f = 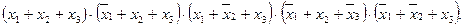
Задание: напишите аналитические выражения для функций f (x1, х2, ..., хп) и φ (х1, x2, ..., хп), заданных таблицей истинности (см. табл. 1).
В системах железнодорожной автоматики, телемеханики и связи могут применяться дискретные устройства, закон функционирования которых определен не полностью. В таких устройствах некоторые комбинации сигналов на входы никогда не подаются. Эти комбинации входных сигналов называют неиспользуемыми. Для неиспользуемых входных комбинаций выходные сигналы не определены.
Если значение ФАЛ определено на всех возможных наборах значений ее переменных, то ее называют полностью определенной. В случае числового задания не полностью определенной функции номера неиспользуемых наборов заключают в скобки:
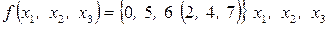 .
.
В булевой алгебре действуют следующие законы:
§ переместительный (коммутативный):
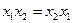 и
и 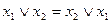 ;
;
§ сочетательный (ассоциативный):
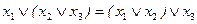 и
и 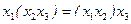 ;
;
§ распределительный (дистрибутивный):
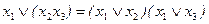 и
и 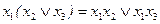 .
.
§ нулевого множества:
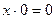 ;
;
§ единичного множества:
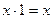 ;
;
§ логического нуля:
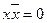 ;
;
§ логической единицы:
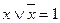 ;
;
§ повторения:
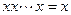 и
и 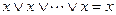 ;
;
§ двойного отрицания:
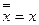 ;
;
§ склеивания:
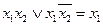 и
и 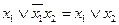 ;
;
§ поглощения:
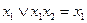 ;
;
§ инверсии, правило де Моргана:
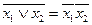 и
и 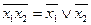 .
.
