При выполнении арифметических операций в ЭВМ применяют прямой, обратный и дополнительный коды
Кодомназывают такую запись числа, которая отличается от естественной и общепринятой. В математике естественной формой записи числа является запись, при которой непосредственно перед старшей значащей цифрой числа помещается знак плюс (+) или минус (-), а длина записи определяется величиной числа (иначе, количество символов, использованных для записи разных чисел, как правило, не совпадает). В ЭВМ это не так. Одной из важнейших характеристик любой ЭВМ является длина слова в ней. Длина слова определяется количеством двоичных разрядов слова, поэтому в ЭВМ, вне зависимости от величины числа, его код всегда имеет фиксированное количество двоичных цифр.
В двоичном алфавите нет никаких символов, кроме цифр 0 и 1, и необходимы новые правила для указания знака числа. Суть этих правил сводится к тому, что знак плюс изображается цифрой 0, знак минус - цифрой 1, а цифра, изображающая знак, всегда записывается самой первой в записи числа. Код числа всегда содержит изображение его знака, в отличие от математической записи, которая позволяет опускать знак плюс при изображении положительного числа. Так, код 011101, согласно этим правилам, изображает положительное (самая левая цифра - 0) двоичное число 11101.
Для более простой и экономичной реализации АЛУ применяют несколько разных кодов чисел. Это связано с тем, что разные операции в ЭВМ более просто реализуются в разных кодах.
Прямой код двоичного числа - это само двоичное число, в котором все цифры, изображающие его значение, записываются как в математической записи, а знак числа записывается двоичной цифрой. При этом никакого символа, отделяющего эту цифру от старшей цифры, используемой при изображении его величины, не допускается. В таких случаях говорят о том, что назначение цифры в коде определяется его позицией.
Пример:
Изображаемое число Код
· +1101 (+13) 0000 1101
· +1011101 (+93) 0101 1101
· 1101 (-13) 1000 1101
(В примере коды изображаются восемью цифрами)
Прямой код почти не отличается от принятого в математике: для выявления абсолютной величины (модуля) числа, надо отбросить цифру, обозначающую его знак. Прямой код используется при хранении чисел в памяти ЭВМ, а также при выполнении операций умножения и деления. Однако применительно к операциям сложения и вычитания такой код неудобен: правила счета для положительных и отрицательных чисел различаются.
Обратный код положительного числа совпадает с прямым, а при записи отрицательного числа все его цифры, кроме цифры, изображающей знак числа, заменяются на противоположные (0 заменяется на 1, а 1 - на 0).
Примеры записи.
Изображаемое число Код
· +1101 (+13) 0000 1101
· +1011101 (+93) 0101 1101
· 1101 (-13) 1111 0010
В этом коде, как к положительным, так и к отрицательным числам можно применять одни и те же правила, а операцию вычитания (А-В) можно заменить операцией сложения (А+(-В)).
Для восстановления прямого кода отрицательного числа из обратного кода надо все цифры, кроме цифры, изображающей знак числа, заменить на противоположные.
Дополнительный код положительного числа совпадает с прямым, а код отрицательного числа образуется как результат увеличения на 1 его обратного кода. (Процесс построения дополнительного кода отрицательного числа можно разбить на два этапа – построить обратный код, а затем из него построить дополнительный).
Пример:
Число -> - 101101
Прямой код -> 1101101
Обратный код -> 1010010
+1
Дополнительный -> 1010011
Для восстановления прямого кода числа из дополнительного нужно полностью повторить (и именно в том же порядке) действия, которые использовались при переводе из прямого в дополнительный код: сначала все цифры, кроме цифры, изображающей знак, заменить на противоположные, а затем прибавить 1.
Сложение и вычитание чисел в обратном и дополнительном кодах выполняется с использованием обычного правила арифметического сложения многоразрядных чисел, при этом разряды, изображающие знаки чисел, рассматриваются как равноправные разряды двоичного числа, которые складываются друг с другом и с единицей переноса из предыдущего разряда числа по обычным правилам арифметики. Различия же обратного и дополнительного кодов связаны с тем, что делается с единицей переноса из старшего разряда. При сложении чисел в дополнительном коде единица переноса из старшего разряда игнорируется (теряется), а в обратном коде эту единицу надо прибавить к младшему разряду результата.
Основным достоинством дополнительного кода является то, что в нем единообразно реализуются операции сложения чисел разных знаков (алгебраическое сложение), а операцию вычитания можно свести к операции сложения заменой знака вычитаемого на обратный.
Практически все современные цифровые ЭВМ в качестве основной используют двоичную систему счисления. При этом все арифметические операции над двоичными числами можно свести к двум элементарным - сложению и сдвигу двоичных кодов, изображающих числа. Это позволит технически реализовать четыре действия арифметики в одном устройстве, называемом арифметико-логическом (АЛУ), используя одни и те же электрические схемы.
Арифметические действия с двоичными числами просты:
| 0 + 0 = 0 | 0 х 0 = 0 |
| 0 + 1 = 1 | 0 х 1 = 0 |
| 1 + 1 = 0 (единица переходит в старший разряд) | 1 х 1 = 1 |
Сумматор — комбинационное устройство, предназначенное для сложения чисел, подставленных в двоичной форме.
Рассмотрим сложение двух одноразрядных двоичных чисел, для чего составим таблицу сложения (таблицу истинности), в которой отразим значения входных чисел X1 и X2, значение результата суммирования S и значение переноса в старший разряд Р:
| X1 | X2 | S | P |
Работа устройства, реализующего данную таблицу истинности, описывается следующими уравнениями: 
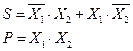
Очевидно, что по отношению к столбцу S реализуется логическая функция «исключающее ИЛИ», т. е. 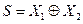 .
.
Устройство, реализующее данную таблицу истинности, называют полусумматором. Оно имеет следующую логическую структуру:
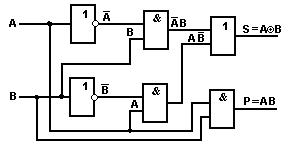
Рис. 6.1. Полусумматор
Поскольку полусумматор имеет только два входа, он может использоваться для суммирования лишь в младшем разряде. При суммировании двух многоразрядных чисел для каждого разряда (кроме младшего) необходимо использовать устройство, имеющее дополнительный вход переноса. Такое устройство называют полным сумматором и его можно представить как объединение двух полусумматоров.
Для этого в каждом из разрядов применяют одноразрядный суммирующий элемент (рис.6.2.) на три входа: два — для слагаемых x1 и x2 данного разряда, а третий (y1) — для переноса 1 из соседнего младшего разряда. Устройство снабжают двумя выходами: по одному (S) выдается искомая сумма (x1+x2), а по другому (Р) переносится 1 в соседний старший разряд.
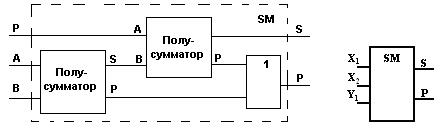
Рис. 6.2. Схема и условное обозначение сумматора.
Для сложения двоичных чисел с несколькими разрядами используют двух- и трехразрядные сумматоры с последовательным переносом 1 в старшие разряды (например, микросхемы К155ИМ2 и К155ИМЗ соответственно). Быстродействие сумматоров последовательного действия лимитируется временем переноса 1 через все элементы устройства. Для улучшения этого показателя применяют сумматоры с параллельным переносом.
