Методы поиска решений. Целесообразность вывода метода поиска решений
Исчисление высказываний. Правила вывода. Нормальные формы.
Исчисление высказываний – это аксиоматическая логическая система, интерпретацией которой является алгебра высказываний. Описание всякого исчисления включает в себя описание символов этого исчисления (алфавита); формул, являющихся конечными конфигурациями символов и определение выводимых формул. Алфавит исчисления высказываний состоит из символов трех категорий: Символы первой категории: x, y, z,…,x1, x2,…, которые называются переменными высказывания; Символы второй категории: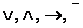 
, которые называются логическими связками. 
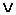– дизъюнкция (логическое сложение), 
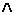– конъюнкция (логическое умножение), → – импликация (логическое следование), ¯ – отрицание; Символы третьей категории: скобки. Других символов исчисление высказываний не имеет. Формулы исчисления высказываний представляют собой последовательности символов алфавита исчисления высказываний. Для обозначения формул будем пользоваться заглавными буквами латинского алфавита. Эти буквы не являются символами исчисления. Они представляют собой условные обозначения формул.
Методы поиска решений. Целесообразность вывода метода поиска решений.
Требования пользователя к результату задачи, решаемой с помощью поиска, можно характеризовать 1) количеством решений : одно решение, несколько решений, все решения. 2) свойствами результата: ограничения, которым должен удовлетворять полученный результат 3) и (или) способом его получения. Существующие методы решения задач, используемые в экспертных системах, можно классифицировать следующим образом: методы поиска в одном пространстве - методы, предназначенные для использования в следующих условиях: области небольшой размерности, полнота модели, точные и полные данные; методы поиска в иерархических пространствах - методы, предназначенные для работы в областях большой размерности; методы поиска при неточных и неполных данных ; методы поиска, использующие несколько моделей, предназначенные для работы с областями, для адекватного описания которых одной модели недостаточно. Предполагается, что перечисленные методам при необходимости должны объединяться для того, чтобы позволить решать задачи, сложность которых возрастает одновременно по нескольким параметрам. Методы поиска решений в одном пространстве обычно делятся на: 1) поиск в пространстве состояний (рассмотрим подробно), 2) поиск методом редукции, 3) эвристический поиск
4) поиск методом "генерация-проверка".
Задачу поиска в пространстве состояний можно сформулировать в общем виде так: Пусть исходная задача описывается тройкой (S, F, T), где S – множество начальных состояний; F – множество операторов, отображающих одни состояния в другие; T – множество целевых состояний. Решение задачи состоит в нахождении последовательности операторов f1,f2,…,fk (fi ÎF), которые преобразуют начальные состояния в конечные. Задача поиска в пространстве состояний описывается с помощью понятий теории графов [41]. Задается начальная вершина (исходное состояние) и множество целевых вершин T. Для построения пространства состояний используются операторы F. Последовательно от корня к вершинам дерева применяются операторы, относящиеся к этому уровню, для построения вершин-преемников следующего уровня (раскрытие вершин). Дуги идентифицируются как операторы преобразования. Получаемые вершины - преемники проверяются: не являются ли они целевыми. Далее переходят к следующему уровню. Терминальные вершины – это те, к которым нельзя применить никаких операторов. Раскрытие продолжается до тех пор, пока не получена целевая или терминальная вершина. Поиск на графе состояний – это процесс построения графа G, содержащего целевую вершину. Этот граф называется графом поиска. Различие нескольких вариантов реализации метода перебора, которые отличаются заданным порядком, в котором будут перебираться вершины (поиск в глубину, поиск в ширину, поиск на основе стоимости дуг, поиск с возвратом). При поиске методом редукции решение задачи сводится к решению совокупности образующих ее подзадач. Этот процесс повторяется для каждой подзадачи до тех пор, пока каждая из полученного набора подзадач, образующих решение исходной задачи, не будет иметь очевидное решение. Процесс решения задачи разбиением ее на подзадачи можно представить в виде специального направленного графа G, называемого И/ИЛИ-графом; Каждой вершине этого графа ставитсяв соответствие описание некоторой задачи (подзадачи). В графе выделяют два типа вершин: конъюнктивные вершины и дизъюнктивные вершины. Решение задачи при поиске методом редукции (при поиске в И/ИЛИ-графе) сводится к нахождению в И/ИЛИ-графе решающего графа. Эвристический поиск - При увеличении пространства поиска методы слепого поиска требуют чрезмерных затрат времени и (или) памяти. Это привело к созданию эвристических методов поиска, т.е. методов, использующих некоторую информацию о предметной области для рассмотрения не всего пространства поиска, а таких путей в нем, которые с наибольшей вероятностью приводят .кцели. Поиск методом "генерация-проверка может быть сформулирован в терминах "генерация-проверка". Для осуществления процесса поиска необходимо генерировать очередное возможное решение (состояние или подзадачу) и проверить, не является ли оно результирующим.