Расчет безотказности последовательной системы

ПРИ НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ НАГРУЗКИ

Цель работы:

1. Изучить методику расчета безотказной работы узла как последовательной системы.

2. Научиться рассчитывать вероятность безотказной работы системы узла редукторного типа.

Общие положения

Если рассеяние нагрузки по системам пренебрежимо мало, а несущие способности элементов независимы друг от друга, то отказы элементов статистически независимы и поэтому вероятность Р (R/F₀) безотказной работы последовательной системы с несущей способностью R при нагрузке F₀ равна произведению вероятностей безотказной работы элементов:

P(R/F₀)= ,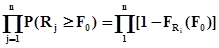

где P(R_j/F₀) – вероятность безотказной работы j-го элемента при нагрузке F₀; n – число элементов в системе; F_Rj(F₀) – функция распределения несущей способности j-го элемента при значении случайной величины R_j, равном F₀.

В большинстве случаев нагрузка имеет существенное рассеяние по системам, например, универсальные машины (станки, автомобили и др.) могут эксплуатироваться в разных условиях. При рассеянии нагрузки по системам, оценку вероятности безотказной работы системы P(R/F) в общем случае следует находить по формуле полной вероятности, разбив диапазон рассеяния нагрузки на интервалы F. Найдя для каждого интервала нагрузки произведение вероятности безотказной работы P(R_j/F_j) у j-го элемента при фиксированной нагрузке на вероятность этой нагрузки f(F_i) F, а затем, просуммировав эти произведения по всем интервалам,

P(R/F)= ,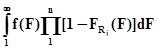

где f(F) – плотность распределения нагрузки; F_Rj(F) – функция распределения

несущей способности j-го элемента при значении несущей

способности R_j=F.

Такие расчеты в общем случае трудоемки, так как предполагают численное интегрирование, а поэтому при большом n возможны только на ЭВМ.

Рассматривается достаточно точный метод упрощенной оценки надежности последовательной системы для случая нормального распределения нагрузки по системам. Идея метода состоит в аппроксимации закона распределения несущей способности системы, так как именно эти значения определяют величину показателя надежности системы.

Сравнительные расчеты на ЭВМ и предлагаемому упрощенному методу показали, что его точность достаточна для инженерных расчетов надежности систем, у которых коэффициент вариации несущей способности не превышает 0,1…0,15, а число элементов системы не превышает 10…15.

Расчеты осуществляются в следующей последовательности:

1. Задаются двумя значениями F_A и F_B фиксированных нагрузок. Проводят расчет вероятностей безотказной работы системы при этих нагрузках. Нагрузки подбирают с тем расчетом, чтобы при оценке надежности системы вероятность безотказной работы системы получилась в пределах P(R/F_A)=0,45…0,60 и P(R/F_B)=0,95…0,99, т.е. охватывали бы представляющий интерес интервал. Ориентировочные значения нагрузок можно принимать близкими значениям F_A»(1+3v_F)m_F, F_B»(1+v_F)m_F.

2. Находят квантили нормального распределения up_A и up_B, соответствующие найденным вероятностям.

3. Аппроксимируют закон распределения несущей способности системы нормальным распределением с параметрами математического ожидания m_R и коэффициента вариации v_R. Пусть S_R – среднее квадратическое отклонение аппроксимирующего распределения. Тогда m_R-F_A+up_AS_R=0 и m_R-F_B+up_BS_R=0. Из приведенных выражений получаем для m_R и v_R=S_R/m_R:

m_R=F_А- ;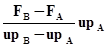

v_R=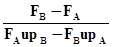

4. Вероятность безотказной работы системы P(R/F) для случая нормального распределения нагрузки F по системам с параметрами математического ожидания m_R и коэффициента вариации v_R находят обычным способом по квантили нормального распределения up. Квантиль up вычисляют по формуле, отражающей факт, что разность двух распределенных нормально случайных величин (несущей способности системы и нагрузки) распределена нормально с математическим ожиданием, равным разности их математических ожиданий и средним квадратическим, равным корню из суммы квадратов их средних квадратических отклонений:

up=- ,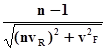

где n=m_R/m_F – условный запас прочности по средним значениям несущей способности и нагрузки.

Порядок выполнения работы

1. Оценить вероятность безотказной работы одноступенчатого редуктора.

2. Пример расчета.

Требуется оценить вероятность безотказной работы одноступенчатого редуктора, если известно следующее. Условные запасы прочности по средним значениям несущей способности и нагрузки составляют: зубчатой передачи n₁=1,5; подшипников входного вала n₂=n₃=1,4; подшипников выходного вала n₄=n₅=1,6; выходного и входного валов n₆=n₇=2,0. Это соответствует математическим ожиданиям несущей способности элементов m_R1=1,5 m_F; m_R2=m_R3=1,4m_F; m_R4=m_R5=1,6; m_R6=m_R7=2m_F. Часто в редукторах n₆ и n₇ соответственно m_R6 и m_R7 существенно больше. Задано, что несущие способности передачи, подшипников и валов нормально распределены с одинаковыми коэффициентами вариации v_R1=v_R2=…= v_R7=0,1, а нагрузка по редукторам распределена также нормально с коэффициентом вариации v_F=0,1.

Задаемся нагрузками F_A и F_В. Принимаем F_A=1,3m_F, F_В=1,1m_F, предполагая, что эти значения дадут близкие к требуемым значениям вероятностей безотказной работы систем при фиксированных нагрузках P(R/F_A) и P(R/F_В).

Вычисляем квантили нормального распределения всех элементов, соответствующие их вероятностям безотказной работы при нагрузках F_A и F_В:

up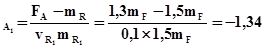

Аналогично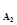, up =up 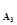=-0,715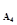; up =up 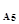=-1,88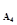; up =up 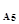=-3,5;

up 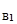=-2,67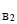; up =up 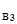=-2,15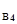; up =up 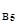=-3,13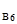; up =up 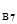=-4,5.

По квантилям из таблицы (Приложение 1) находим вероятность безотказной работы элементов: P₁(R/F_A)=0,9099; P₂(R/F_A)=P₃(R/F_A)=0,7627;

P₄(R/F_A)= =P₅(R/F_A)=0,9699; P₆(R/F_A)=P₇(R/F_A)=0,9998 при нагрузке F_A и P₁(R/F_В)=0,9967; P₂(R/F_В)=P₃(R/F_В)=0,9842;

P₄(R/F_В)=P₅(R/F_В)=0,9991; P₆(R/F_В)=P₇(R/F_В)=1,000 при нагрузке F_В.

Вероятность безотказной работы редуктора P(R/F_A) и P(R/F_В) при фиксированных нагрузках F_A и F_В оцениваем по формуле как произведение вероятностей безотказной работы элементов. Получаем P(R/F_A)=0,4979; P(R/F_В)=0,9637. Сопоставляя эти значения с диапазонами допустимых значений, приведенными выше, видим, что вероятности находятся внутри диапазонов. Поэтому изменять значения F_A и F_В не будем.

Вычисляем математическое ожидание m_R и коэффициент вариации v_R несущей способности редуктора:

m_R=F_A- ;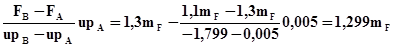

v_R= ,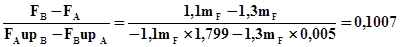

где up_A, up_B квантили нормального распределения, соответствующие вероятностям P(R/F_A) и P(R/F_В).

Вычисляем квантиль up нормального распределения, соответствующую вероятности P(R/F) безотказной работы редуктора:

up=-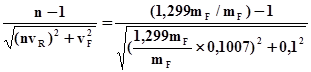

Находим искомую вероятность, соответствующую полученной квантили: P(R/F)=0,965.

Таблица 1

Варианты заданий

№ вари анта	Условные запасы прочности по средним значениям несущей способности и нагрузки	Коэффициенты вариации
Зубчатая передача, n1	Подшипники входного вала, n2=n3	Подшипники выходного вала, n4=n5	Входной и выходной вал, n6=n7	Несущей способности, vRi	Нагрузки, vF
	1,5	1,4	1,6	1,9	0,1	0,11
	1,4	1,6	1,5	2,0	0,11	0,1
	1,6	1,5	1,4	2,1	0,12	0,11
	1,45	1,6	1,55	1,9	0,11	0,12
	1,5	1,45	1,6	2,2	0,11	0,12
	1,6	1,55	1,45	2,0	0,1	0,12
	1,4	1,6	1,55	1,9	0,12	0,1
	1,45	1,55	1,4	2,1	0,11	0,12
	1,55	1,5	1,45	1,9	0,1	0,11
	1,5	1,4	1,5	2,0	0,12	0,11

ПРИЛОЖЕНИЯ

Приложение 1

Таблица значений интегральной функции нормального закона.

Доля общей площади под кривой плотности нормального распределения, соответствующая изменению переменной t от - ¥ до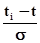

(t_i- действительные значения случайной величины t)

	0,09	0,08	0,07	0,06	0,05	0,04	0,03	0,02	0,01	0,00
-3,5	0,00017	0,00017	0,000I8	0,00019	0,00019	0,00020	0,00021	0,00022	0,00022	0,00023
-3,4	0,00024	0,00025	0,00026	0,00027	0,00028	0,00029	0,00030	0,0003I	0,00033	0,00034
-3,3	0,00035	0,00036	0,00038	0,00039	0,00040	0,00042	0,00043	0,00043	0,00047	0,00048
-3.2	0,00050	0,00052	0,00054	0,00056	0,00058	0,00060	0,00062	0,00064	0,00066	0,00069
-3,1	0.00071	0,00074	0,00076	0,00079	0,00082	0,00085	0,00087	0,00090	0,00094	0,00097
-3,0	0,00100	0,00104	0,00107	0,00111	0,00114	0,00118	0,00122	0,00126	0,00131	0,00135
-2,9	0,0014	0,0014	0,0015	0,0015	0,0016	0,0016	0,0017	0,0017	0,0018	0,00I9
-2,8	0,0019	0,0020	0,0021	0,0021	0,0022	0,0023	0,0023	0,0024	0,0025	0,0026
-2.7	0,0026	0,0027	0,0028	0,0029	0,0030	0,0031	0,0032	0,0033	0,0034	0,0035
-2,6	0,0036	0.0037	0,0038	0,0039	0,0040	0,0041	0,0043	0,0044	0,0045	0,0047
-2,5	0,0048	0,0049	0,0051	0,0052	0,0054	0,0055	0.0057	0,0059	0,0060	0,0062
-2,4	0,0064	0.0066	0,0068	0,0069	0,0071	0,0073	0,0075	0,0078	0,0080	0,0082
-2,3	0,0084	0,0087	0.0089	0,0091	0,0094	0,0096	0,0099	0,0102	0,0104	0,0107
-2,2	0,0110	0,0113	0,0116	0,0119	0,0122	0,0125	0,0129	0,0132	0,0I36	0,0139
-2,1	0,0143	0,0146	0,0150	0,0154	0,0158	0,0162	0,0166	0,0I70	0,0174	0.0179

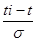0,09 0.08 0,07 0.06 0,05 0.04 0.03 0,02 0,01 0.00	0,09	0,08	0,07	0,06	0,05	0,04	0,03	0,02	0,01	0,00
-2,0	0,0183	0,0188	0,0192	0,0197	0,0202	0,0207	0,0212	0,0217	0,0222	0,0228
-1,9	0,0233	0,0239	0,0244	0,0250	0,0256	0,0262	0,0268	0,0274	0,0281	0,0287
-1,8	0,0294	0,030I	0,0307	0,0314	0,0322	0,0329	0,0336	0,0344	0,0351	0,0359
-1,7	0,0367	0,0375	0,0384	0,0392	0,0401	0,0409	0,0418	0,0427	0,0436	0,0446
-1,6	0,0455	0,0465	0,0475	0,0485	0,0495	0,0505	0,0516	0,0526	0,0537	0,0548
-1,5	0,0559	0,0571	0,0582	0,0594	0,0606	0,0618	0,0630	0,0643	0,0655	0,0668
-1,4	0,0681	0,0694	0,0708	0,0721	0,0735	0,0749	0,0764	0,0778	0,0793	0,0808
-1,3	0,0823	0,0838	0,0853	0,0869	0,0885	0,0901	0,0918	0,0934	0,0951	0,0968
-1,2	0,0985	0,1003	0,1020	0,1038	0,1057	0,1075	0,1093	0,1112	0,1131	0,1151
-1,1	0,1170	0,1190	0,1210	0,1230	0,1251	0,1271	0,1292	0,1314	0,1335	0,1357
-1,0	0,1379	0,1401	0,1423	0,1446	0,1469	0,1492	0,1515	0,1539	0,1562	0,1587
-0,9	0,1611	0,1635	0,1660	0,1685	0,1711	0,1736	0,1762	0,1788	0,1814	0,1841
-0,8	0,1867	0,1894	0,1922	0,1949	0,1977	0,2005	0,2033	0,2061	0,2090	0,2119
-0,7	0,2148	0,2177	0,2207	0,2236	0,2266	0,2297	0,2327	0,2358	0,2389	0,2420
-0,6	0,2451	0,2483	0,2514	0,2546	0,2578	0,2611	0,2643	0,2676	0,2709	0,2743
-0,5	0,2776	0,2810	0,2843	0,2877	0,2912	0,2946	0,2981	0,3015	0,3050	0,3085
-0,4	0,3121	0,3156	0,3192	0,3228	0,3264	0,3300	0,3336	0,3372	0,3409	0,3446
-0,3	0,3483	0,3520	0,3557	0,3594	0,3632	0,3669	0,3707	0,3745	0,3783	0,3821
-0,2	0,3859	0,3897	0,3936	0,3974	0,4013	0,4052	0,4090	0,4129	0,4168	0,4207
-0,1	0,4247	0,4286	0,4325	0,4364	0,4404	0,4443	0,4483	0,4522	0,4562	0,4602
-0,0	0,4641	0,4681	0,4721	0,4761	0,4801	0,4840	0,4880	0,4920	0,4960	0,5000

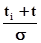	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
+0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
+0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753
+0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141
+0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
+0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6808	0,6844	0,6879
+0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
+0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549
+0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
+0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023	0,8051	0,8079	0,8106	0,8133
+0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
+1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
+1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830
+1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,8980	0,8997	0,9015
+1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177
+1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319
+1,5	0,9332	0,9345	0,9357	0,9370	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441
+1,6	0,9452	0,9463	0,9447	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545
+1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9599	0,9608	0,9616	0,9625	0,9633
+1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706
+1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,9750	0,9756	0,9761	0,9767
+2,0	0,9773	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817

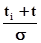	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
+2,1	0,9821	0,9826	0,9830)	0,9834	0,9838	0,9842	0,9846	0,9850	0,9854	0,9857
+2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,9890
+2,3	0,9893	0,9896	0,9898	0,9901	0,9904	0,9906	0,9909	0,9911	0,9913	0,9916
+2,4	0,9918	0,9920	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936
+2,5	0,9938	0,9940	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952
+2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,9960	0,9961	0,9962	0,9963	0,9964
+2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972	0,9973	0,9974
+2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,9980	0,9981
+2,9	0,9981	0,9982	0,9983	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986	0,9986
+3,0	0,99865	0,99869	0,99874	0,99878	0,99882	0,99886	0,99889	0,99893	0,99896	0,99900
+3,1	0,99903	0,99906	0,99910	0,99913	0,99915	0,99918	0,99921	0,99924	0,99926	0,99929
+3,2	0,99931	0,99934	0,99936	0,99938	0,99940	0,99942	0,99944	0,99946	0,99948	0,99950
+3.3	0,99952	0,99953	0,99955	0,99957	0,99958	0,99960	0,99961	0,99962	0,99964	0,99965
+3,4	0,99966	0,99967	0,99969	0,99970	0,99971	0,99972	0,99973	0,99974	0,99975	0,99976
+3,5	0,99977	0,99978	0,99978	0,99979	0,99980	0,99981	0,99981	0,99982	0,99983	0,99983

Приложение 2