C) связный граф без циклов

$$$ 129

Пусть Х и Y - два множества, |X|=3, |Y|=5. Сколько существует инъективных отображений X®Y?

E) 60

$$$ 130

Пусть Х и Y - два множества, |X|=3, |Y|=5. Сколько существует функциональных отображений X®Y ?

B) 125

$$$ 131

На множестве А= {1, 2, 3, 4} задано бинарное отношение {(1,3), (1,4), (3, 1), (4, 1), (2,3)}. Является ли оно 1)рефлексивным, 2)антирефлексивным, 3)симметричным, 4)антисимметричным, 5)транзитивным?

A) 1) нет 2) да 3) нет 4) нет 5) нет

$$$ 132

Функции f(x₁, _…,x_n) и g(x₁,…,x_n) называются двойственными друг другу, если для всех наборов значений переменных выполняется равенство

D) f(x₁, …, x_n) =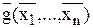

$$$ 133

Дуга транспортной сети называется насыщенной, если

B) поток на ней равен пропускной способности

$$$ 134

Какой граф называется гамильтоновым?

C) содержащий простой цикл, проходящий через все вершины графа

$$$135

Граф называется ориентированным, если

B) он содержит только дуги

$$$ 136

Вершины графа называются смежными, если

B) они соединены ребром или дугой

$$$ 137

Диаметр графа - это

C) самое большое расстояние в графе

$$$ 138

Цикломатическое число графа показывает

D) количество независимых циклов графа

$$$ 139

Хроматическое число графа показывает

A) минимальное число красок, необходимое для правильной раскраски графа

$$$ 140

Радиус графа - это

E) максимальное удаление от центра

$$$ 141

Сколькими способами можно раскрасить квадрат, разделенный на четыре части, если имеется пять различных красок и не допускается раскрашивание разных частей в один цвет?

E) 120

$$$ 142

Логическая функция f(x,y) задана своими значениями на последовательности наборов значений аргументов (0,0), (0,1), (1,0), (1,1): f = ( 0 0 1 1 ). Найдите ее совершенную дизъюнктивную нормальную форму (СДНФ).

D) х& V х&y

$$$ 143

Укажите эквивалентные формулы:

1) 2) 3)

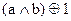
A) 2, 3

$$$ 144

Какая из приведенных систем логических функций является функционально полной?

D) {x&y, x y, 1}

$$$ 145

Совершенная дизъюнктивная нормальная форма (СДНФ) логической функции f(x,y)= x ~ y имеет вид

A) x &y V &

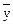
$$$ 146

Пусть Х- множество, |X|=5. Сколько существует инъективных отображений этого множества в себя?

B) 120

$$$ 147

В матрице указаны веса ребер связного неориентированного четырехвершинного графа. Найдите вес минимального остовного дерева.

¥ 5 7 6

5 ¥ 2 4

7 2 ¥ 3

6 4 3 ¥

B) 10

$$$ 148

Найдите цикломатическое число графа, заданного множеством вершин X={1, 2, 3, 4, 5} и отношением на этом множестве: 5≤| x+y | ≤8.

C) 3

$$$ 149

Пусть Х - множество, |X|=6. Сколькими способами можно разбить это множество на 3 подмножества таких, что первое из них содержит 3 элемента, второе - 2 элемента, третье - 1 элемент?

D) 60

$$$ 150

Какой граф называется неориентированным?

C) граф, содержащий только ребра

$$$ 151

Какое из перечисленных множеств не является счетным?