Для расчета среднего квадратического отклонения результата измерения используется формула
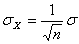. (3.3)
Среднее квадратическое отклонение результата измерения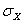 
является основной характеристикой размера случайных погрешностей результата измерений.
Основными понятиями при статистических оценках являются понятия доверительного интервала и доверительной вероятности.
Доверительным интервалом называется интервал, в который с заданной доверительной вероятностью попадают значения случайной величины (погрешности). Доверительный интервал выражается в виде
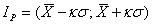, (3.4)
где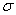 
- среднее квадратическое отклонение результата наблюдения;
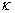- квантильный множитель, значение которого зависит от выбранного закона распределения случайной погрешности.
Так для равномерного закона распределения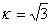 
и не зависит от доверительной вероятности. Для нормального закона распределения 
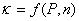зависит от значения доверительной вероятности Р и количества выборочных значений n ; значения 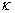для наиболее употребительных доверительных вероятностей Р и различных n приведены в таблице П1-4-1 [1].
Доверительные границы случайной погрешности 
x, соответствующие доверительной вероятности Р, находят по формуле 
.
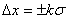Значение и знак случайной погрешности определить невозможно. Для учета случайной погрешности проводят многократные (статистические) измерения. Оценивая случайную погрешность, говорят об ожидаемой погрешности. Грубая погрешность – это случайная погрешность, существенно превышающая ожидаемую погрешность при данных условиях. Промах – погрешность, которая явно искажает результат измерения. За промах принимают случайную субъективную погрешность экспериментатора.
Доверительному интервалу ±3 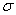соответствует Р = 0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3 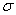предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи. Грубые погрешности и промахи обычно исключаются из экспериментальных данных до начала статистической обработки результатов наблюдений.
3.1.2 Задача №1
В результате проведенных измерений оказалось, что наиболее вероятное содержание кислорода в газовой смеси составляет Х=11,75%. Доверительный интервал погрешности измерения определялся для доверительной вероятности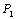 
= 0,683 и составил 
= 
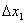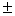0,5%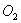 
.
Определить границы доверительного интервала при доверительной вероятности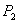 
= 0,95, если известно, что закон распределения погрешностей нормальный.
Варианты индивидуальных заданий приведены в Приложении В, таблица В1.
3.1.2.1 Пример решения задачи №1
При нормальном законе распределения погрешностей при доверительной вероятности 0,683 доверительные границы случайной погрешности определяют по таблице П1-4-1 [1] :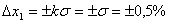 
. При доверительной вероятности 0,95 
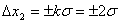. Таким образом, числовое значение доверительного интервала для доверительной вероятности 0,95 составит 
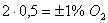. Границы доверительного интервала по (3.4) будут равны
.
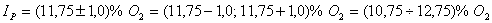Ответ: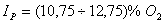 
.
3.1.3 Задача №2
Определить границы доверительного интервала погрешности измерения температуры с вероятностью Р, если при большом числе измерений были получены среднее арифметическое результата наблюдений 
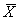и дисперсия 
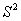. Предполагается нормальный закон распределения погрешности.
Варианты индивидуальных заданий приведены в Приложении В, таблица В2.
3.1.4 Задача № 3
В результате большого числа измерений термо-ЭДС был определен доверительный интервал 
, мВ, с доверительной вероятностью Р. Определить среднюю квадратическую погрешность 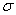измерения термо-ЭДС в предположении нормального закона распределения погрешности.
Варианты индивидуальных заданий приведены в Приложении В, таблица В3.
Задание №2
3.2.1 Стандартная методика обработки результатов прямых
измерений с многократными независимыми наблюдениями
В измерительной практике для повышения качества измерений часто обращаются к измерениям с многократными наблюдениями, т.е. к повторению одним и тем же оператором однократных наблюдений в одинаковых условиях с использованием одного и того же средства измерения. В результате соответствующей обработки полученных данных удается уменьшить влияние случайной составляющей погрешности на результат измерений. При этом могут быть использованы различные процедуры обработки результатов наблюдений. Ниже описана стандартная методика обработки результатов прямых измерений с многократными, независимыми наблюдениями и основные положения по оцениванию погрешностей результатов измерений. Эта методика соответствует рекомендациям действующего ГОСТ 8.207-76 «Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений».
В соответствии с методикой обработку ряда наблюдений следует выполнять в следующей последовательности:
а) исключить известные систематические погрешности из результатов наблюдений;
б) вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;
в) вычислить оценку среднего квадратического отклонения результатов наблюдения;
г) вычислить оценку среднего квадратического отклонения результатов измерения;
д) исключить грубые погрешности и промахи из результатов наблюдений;
е) в случае обнаружения грубых погрешностей и промахов после их исключения, повторить б)-г);
ж) проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению;
з) вычислить доверительные границы случайной составляющей погрешности результата измерения;
и) вычислить границы неисключенной систематической погрешности результата измерения;
к) вычислить доверительные границы погрешности результата измерения;
л) представить результат измерения в соответствии с установленными требованиями.
При выполнении этой последовательности действий руководствуются следующими правилами:
- проверку гипотезы о принадлежности результатов наблюдений нормальному распределению проводят с уровнем значимости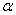 
, выбираемым в диапазоне от 0.02 до 0.1;
- при определении доверительных границ погрешности результата измерения доверительную вероятность Р принимают равной 0.95;
- в тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности Р=0.95, допускается указывать границы для Р=0.99.
3.2.1.1 Исключение систематических погрешностей
Исключение систематических погрешностей из результатов наблюдений проводится либо расчетным путем, либо по результатам поверки. После исключения систематических погрешностей все дальнейшие вычисления проводятся для исправленного ряда наблюдений. В данной задаче считаем систематические погрешности исключенными.
3.2.1.2 Вычисление среднего арифметического ряда наблюдений
Оценка среднего арифметического ряда наблюдений (результатов наблюдений) рассчитывают по формуле (3.1).
3.2.1.3 Вычисление оценки среднего квадратического отклонения ряда наблюдений
Оценка среднего квадратического отклонения ряда наблюдений 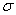рассчитывают по формуле (3.2). Среднее квадратическое отклонение ряда наблюдений 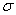является основной характеристикой размера случайных погрешностей результатов наблюдений.
3.2.1.4 Определение и исключение грубых погрешностей или промахов.
Исключить из заданной выборки наблюдений те значения, которые выходят за границы 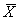±3 .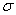
3.2.1.5 Вычисление оценки среднего квадратического отклонения результата измерения
Оценка среднего квадратического отклонения результата измерений 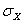рассчитывают по формуле (3.3).
3.2.1.6 Проверка гипотезы о принадлежности результатов наблюдений нормальному распределению
Чтобы установить, принадлежат (или не принадлежат) результаты наблюдений тому или иному распределению, необходимо сравнить экспериментальную функцию распределения с предполагаемой теоретической. Сравнение осуществляется с помощью критериев согласия.
В случае проверки принадлежности результатов наблюдений нормальному распределению предпочтительным при числе результатов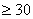 
является один из критериев 
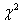Пирсона или 
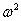Мизеса-Смирнова. В работе используется критерий Пирсона.
При числе результатов наблюдений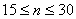 
производят приближенную проверку их принадлежности к нормальному распределению путем оценки коэффициента асимметрии и эксцесса.
При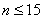 
гипотеза о принадлежности результатов к какому-либо распределению не проверяется. Если при этом имеется априорная информация о том, что нет причин, которые могли бы вызвать заметное отклонение распределения результатов от нормального закона, для обработки результатов наблюдений используется распределение Стьюдента.
Для проверки принадлежности результатов наблюдений к нормальному распределению с помощью критерия согласия Пирсона необходимо сначала построить гистограмму.
Построение гистограммы включает в себя следующие этапы:
а) исправленные результаты наблюдений располагаются в порядке возрастания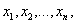 
где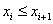 
;
б) вычисляется диапазон изменения значений результатов наблюдений
;
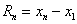в) весь этот диапазон разбивается на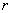 
интервалов одинаковой длины (оценить необходимое количество интервалов можно по правилу 
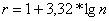с последующим округлением в большую сторону до ближайшего целого нечетного числа). Обычно 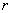лежит в диапазоне 7 
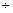15;
г) определяется ширина интервала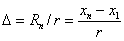 
;
д) определяются границы интервалов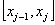 
так, чтобы верхняя граница j–го интервала 
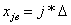, а его нижняя граница совпала с верхней границей (j-1)–го интервала 
;
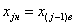е) для каждого j–го интервала (j=1,2, ...,r) вычисляются числа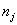 
- частота попадания результата наблюдений в интервал;
ж) строится гистограмма: по оси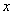 
в порядке возрастания номеров откладываются интервалы 
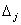, по оси 
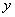откладываются 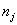-частота попадания результатов наблюдений в j–ый интервал; таким образом на каждом интервале 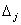строится прямоугольник, высота которого пропорциональна 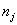. По результатам анализа гистограммы высказывается гипотеза о виде закона распределения экспериментальных данных и о численных характеристиках этого закона (для нормального закона такими характеристиками являются математическое ожидание и дисперсия). После этого используют критерий согласия для проверки гипотезы.
Критерий согласия 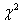Пирсона имеет вид
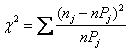, (3.5)
где величина 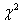характеризует меру отклонения результатов наблюдений от теоретически предсказанных;
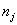- частота попадания результатов наблюдений в 
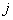–ый интервал;
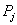- теоретические значения вероятности попадания результатов в 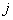- интервал, которые вычисляются по формуле
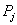
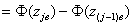, (3.6)
где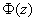 
- функция Лапласа, 
; 
.
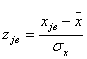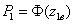Таблица значений функции Лапласа для некоторых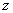 
приведена в Приложении В (таблица В4).
После вычисления значения 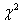для заданной доверительной вероятности Р и числа степеней свободы 
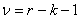(где 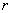- количество разрядов разбиения; 
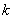- число параметров, необходимых для определения теоретической функции распределения, равное для нормального закона распределения двум), по таблицам 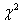распределения находят критическое значение критерия согласия 
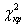. В технической практике обычно задаются Р=0,95, что соответствует вероятности 0,05 совершить ошибку первого рода, т.е. опровергнуть правильную гипотезу. Значения 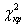приведены в Приложении В (таблица В5).
Если < , принимают гипотезу о том, что результаты наблюдений принадлежат нормальному распределению, характеризующемуся математическим ожиданием и дисперсией, оценки которых получены по формулам (3.1) и (3.3). В противном случае ( ) гипотеза отвергается.
3.2.1.7 Вычисление доверительных границ случайной погрешности результата измерения
Доверительные границы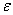 
(без учета знака) случайной погрешности результата измерения находят по формуле
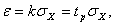(3.7)
где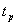 
- квантиль распределения Стьюдента, который зависит от доверительной вероятности Р и числа наблюдений 
.
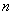Значения величины 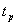при Р=0,95 и 0,99 приведены в Приложении Б (таблица В6).
3.2.1.8 Вычисление границ неисключенной систематической погрешности результата измерения
Неисключенная систематическая погрешность результата измерения образуется из составляющих, которыми могут быть неисключенные систематические погрешности метода, средств измерений и т.п. За границы составляющих неисключенной систематической погрешности принимают, например, пределы основных и дополнительных погрешностей средств измерений. При суммировании составляющие неисключенной систематической погрешности рассматриваются как случайные величины с равномерными законами распределения. Границы неисключенной систематической погрешности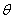 
результата измерения рассчитываются по формуле
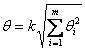, (3.8)
где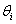 
- граница 
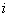-ой неисключенной систематической погрешности;
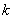- коэффициент, определяемый принятой доверительной вероятностью (при Р=0,95 полагают 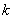=1,1).
3.2.1.9 Вычисление доверительных границ погрешности результата измерения
Доверительная граница погрешности результата измерения устанавливается в зависимости от соотношения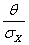 
.
Если 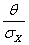<0,8 , то неисключенными систематическими погрешностями пренебрегают и принимают, что доверительная граница погрешности результата измерения 
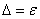(формула 3.7).
Если 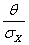>8, то случайной погрешностью пренебрегают и принимают, что доверительная граница погрешности результата измерения 
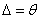(формула 3.8).
Если 0,8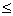 
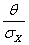
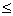8, то доверительные границы погрешности результата измерения вычисляются по формуле
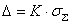, (3.9)
где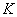 
- коэффициент, зависящий от соотношения случайной погрешности и неисключенной систематической погрешности;
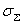- оценка суммарного среднего квадратического отклонения результата измерения.
Коэффициент 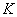рассчитывается по формуле
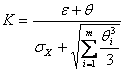. (3.10)
Оценка 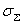осуществляется по формуле
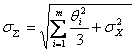. (3.11)
3.2.2 Варианты заданий
В соответствии с приведенной выше методикой (п.3.2.1) провести обработку ряда наблюдений.
Варианты индивидуальных заданий приведены в Приложении В, таблица В7.
Приложение А
Т а б л и ц а А1- РГР №1, варианты задания №1, задача 1
| № варианта | 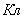 | Диапазон измерений |  |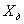
| 0,5 | от 0 В до + 200 В | 127 В | |
| 1,0 | от -10 В до + 10 В | 8 В | |
| 1,5 | от-50 В до + 50 В | 25 В | |
| 2,0 | от 0 В до + 100 В | 60 В | |
| 0,2 | От 0 В до + 50 В | 25 В | |
| 0,5 | от 0  до 600 | 450 | |
| 1,5 | от 0 до 800 | 600 | |
| 1,0 | от 0 до 900 | 750 | |
| 2,0 | от 0 до 1600 | 1100 | |
| 2,5 | от 0 до 900 | 500 | |
| 4,0 | от 0 Ом до 1000 Ом | 500 Ом | |
| 0,2 | от 0 Ом до 500 Ом | 250 Ом | |
| 5,0 | от 0 Ом до 1000 Ом | 850 Ом | |
| 0,1 | от 0 Ом до 1500 Ом | 1000 Ом | |
| 2,5 | от 0 Ом до 2000 Ом | 1750 Ом | |
| 2,0 | от 0 мА до +100 мА | 25 мА | |
| 2,5 | от 0 мА до +150 мА | 50 мА | |
| 1,0 | от –50 мА до +50 мА | 30 мА | |
| 1,5 | от –50 мА до +150 мА | 90 мА | |
| 1,0 | от 0 мА до +50 мА | 10 мА | |
| 2,0 | от 0 кПа до +80 кПа | 40 кПа | |
| 2,5 | от 0 кПа до +100 кПа | 50 кПа | |
| 4,0 | от 0 кПа до +120 кПа | 60 кПа | |
| 2,0 | от 0 кПа до +50 кПа | 30 кПа | |
| 3,0 | от 0 кПа до + 120кПа | 65 кПа |
Т а б л и ц а А2- РГР №1, варианты задания №1, задача 2
| № варианта | 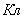| Диапазон измерений |  |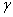
| 1,0 | от -10 В до + 10 В | 1,0 | |
| 1,5 | от-50 В до + 50 В | 1,5 | |
| 2,0 | от 0 В до + 100 В | 2,0 | |
| 0,2 | От 0 В до + 50 В | 0,2 | |
| 0,5 | от 0 до 600 | 0,5 | |
| 1,5 | от 0 до 800 | 1,5 | |
| 1,0 | от 0 до 900 | 1,0 | |
| 2,0 | от 0 до 1600 | 2,0 | |
| 2,5 | от 0 до 900 | 2,5 | |
| Продолжение таблицы А2 | |||
| 4,0 | от 0 Ом до 1000 Ом | 4,0 | |
| 0,2 | от 0 Ом до 500 Ом | 0,2 | |
| 5,0 | от 0 Ом до 1000 Ом | 5,0 | |
| 0,1 | от 0 Ом до 1500 Ом | 0,1 | |
| 2,5 | от 0 Ом до 2000 Ом | 2,5 | |
| 2,0 | от 0 мА до +100 мА | 2,0 | |
| 2,5 | от 0 мА до +150 мА | 2,5 | |
| 1,0 | от –50 мА до +50 мА | 1,0 | |
| 1,5 | от –50 мА до +150 мА | 1,5 | |
| 1,0 | от 0 мА до +50 мА | 1,0 | |
| 2,0 | от 0 кПа до +80 кПа | 2,0 | |
| 2,5 | от 0 кПа до +100 кПа | 2,5 | |
| 4,0 | от 0 кПа до +120 кПа | 4,0 | |
| 2,0 | от 0 кПа до +50 кПа | 2,0 | |
| 3,0 | от 0 кПа до + 120кПа | 3,0 | |
| 0,5 | от 0 В до + 200 В | 0,5 |
Т а б л и ц а А3- РГР №1, варианты задания №1, задача 3
| № варианта | Поверяемая термопара | Образцовая термопара | 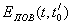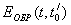 , мВ |  , мВ |  ,  |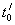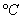
| ТХА | ТПП | 1,26 | 0,187 | ||
| ТХА | ТПП | 3,05 | 0,459 | ||
| ТХА | ТПП | 1,22 | 0,220 | ||
| ТХА | ТПП | 2,72 | 0,496 | ||
| ТХА | ТПП | 5,29 | 0,525 | ||
| ТХА | ТПП | 1,22 | 0,181 | ||
| ТХА | ТПП | 2,88 | 0,453 | ||
| ТХА | ТПП | 1,18 | 0,214 | ||
| ТХА | ТПП | 3,18 | 0,490 | ||
| ТХА | ТПП | 3,09 | 0,599 | ||
| ТХА | ТПП | 1,59 | 0,240 | ||
| ТХА | ТПП | 2,59 | 0,376 | ||
| ТХК | ТПП | 3,35 | 0,342 | ||
| ТХК | ТПП | 4,74 | 0,484 | ||
| ТХК | ТПП | 5,30 | 0,519 | ||
| ТХК | ТПП | 8,42 | 0,902 | ||
| ТХК | ТПП | 2,68 | 0,233 | ||
| ТХК | ТПП | 3,54 | 0,376 | ||
| ТХК | ТПП | 3,39 | 0,315 | ||
| ТХК | ТПП | 4,67 | 0,469 | ||
| ТХК | ТПП | 5,23 | 0,512 |
Продолжение таблицы А3
| ТХК | ТПП | 1,02 | 0,049 | ||
| ТХК | ТПП | 1,92 | 0,169 | ||
| ТХК | ТПП | 3,63 | 0,309 | ||
| ТХК | ТПП | 4,12 | 0,406 |
Т а б л и ц а А4- РГР №1, варианты задания №1, задача 4
| № варианта | Градуировка термосопротивления | 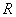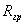 , Ом |  , Ом |
| Гр 23 | 4,5 | 5,0 | |
| Гр 23 | 4,6 | 5,0 | |
| Гр 23 | 4,7 | 5,0 | |
| Гр 23 | 4,8 | 5,0 | |
| Гр 23 | 4,4 | 5,0 | |
| Гр 23 | 4,3 | 5,0 | |
| Гр 23 | 4,2 | 5,0 | |
| Гр 23 | 4,1 | 5,0 | |
| Гр 23 | 4,0 | 5,0 | |
| Гр 23 | 4,9 | 5,0 | |
| Гр 23 | 5,1 | 5,0 | |
| Гр 23 | 5,2 | 5,0 | |
| Гр 24 | 4,5 | 5,0 | |
| Гр 24 | 4,6 | 5,0 | |
| Гр 24 | 4,7 | 5,0 | |
| Гр 24 | 4,8 | 5,0 | |
| Гр 24 | 4,4 | 5,0 | |
| Гр 24 | 4,3 | 5,0 | |
| Гр 24 | 4,2 | 5,0 | |
| Гр 24 | 4,1 | 5,0 | |
| Гр 24 | 4,0 | 5,0 | |
| Гр 24 | 4,9 | 5,0 | |
| Гр 24 | 5,1 | 5,0 | |
| Гр 24 | 5,2 | 5,0 | |
| Гр 24 | 5,3 | 5,0 |
Т а б л и ц а А5- РГР №1, варианты задания №1, задача 5
| № варианта | РОЗ, 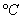| Н.У., 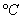| Кл |  , |  , % |  , |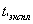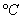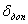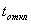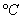
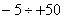 |  | 0,25 | 0,2 | |||
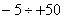| | | 0,5 | 0,2 | |||
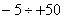| | | 0,3 | 0,2 | |||
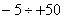| | | 0,4 | 0,2 | |||
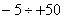| | | 1,0 | 0,2 | |||
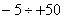| | | 0,25 | 0,15 | |||
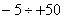| | | 0,5 | 0,15 | |||
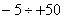| | | 0,3 | 0,15 | |||
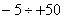| | | 0,4 | 0,15 | |||
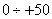 | | 1,0 | 0,15 | |||
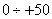| | | 0,25 | 0,25 | |||
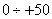| | | 0,5 | 0,25 | |||
| | | 0,3 | 0,25 | |||
| | | 0,4 | 0,25 | |||
| | | 1,0 | 0,25 | |||
| | | 0,25 | 0,3 | |||
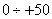| | | 0,5 | 0,3 | |||
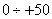| | | 0,3 | 0,3 | |||
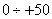| | | 0,4 | 0,3 | |||
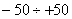 | | 1,0 | 0,3 | |||
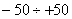| | | 0,25 | 0,1 | |||
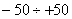| | | 0,5 | 0,1 | |||
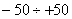| | | 0,3 | 0,1 | |||
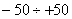| | | 0,4 | 0,1 | |||
| | | 1,0 | 0,1 |
Приложение Б
Т а б л и ц а Б1- РГР №2, варианты задания №1, задача 1
| № варианта | Средство измерения | Класс точности | Диапазон измерений или верхний предел | Показания СИ |
| вольтметр | 0,5 | от 0 В до + 200 В | 127 В | |
| вольтметр | 1,0 | от -10 В до + 10 В | 12 В | |
| вольтметр | 1,5 | от-50 В до + 50 В | 25 В | |
| вольтметр | 2,0 | от 0 В до + 100 В | 60 В | |
| вольтметр | 0,2/0,3 | 50 В | 25 В | |
| потенциометр | 0,5 | от 0 до 600 | 450 | |
| потенциометр | 1,5 | от 0 до 800 | 600 | |
| потенциометр | 1,0 | от 0 до 900 | 750 | |
| потенциометр | 2,0 | от 0 до 1600 | 1100 | |
| потенциометр | 2,5 | от 0 до 900 | 500 | |
| омметр | 4,0 | неравномерная | 50 Ом | |
| омметр | 0,02/0,04 | 500 Ом | 250 Ом | |
| омметр | 5,0 | от 0 Ом до 1000 Ом | 850 Ом | |
| омметр | 0,1/0,02 | 1500 Ом | 1000 Ом | |
| омметр | 2,5 | от 0 Ом до 2000 Ом | 1750 Ом | |
| амперметр | 2,0 | неравномерная | 25 мА | |
| амперметр | 2,5 | неравномерная | 50 мА | |
| амперметр | 1,0 | от –50 мА до +50 мА | 30 мА | |
| амперметр | 1,5 | от –50 мА до +150 мА | 90 мА | |
| амперметр | 0,01/0,01 | 25 мА | 10 мА | |
| манометр | 2,0 | неравномерная | 40 кПа | |
| манометр | 2,5 | неравномерная | 50 кПа | |
| манометр | 4,0 | неравномерная | 60 кПа | |
| манометр | 0,2/0,1 | 40 кПа | 30 кПа | |
| манометр | 0,05/0,02 | 80 кПа | 65 кПа |
Т а б л и ц а Б2 – РГР №2, варианты задания №1, задача 2
| № варианта | Средство измерения | Относительная погрешность,% | Номинальное значение измеряемой величины | Показания средства измерения |
| вольтметр | 1,0 | 127 В | 130 В | |
| вольтметр | 1,5 | 12 В | 10 В | |
| вольтметр | 1,0 | 25 В | 26 В | |
| вольтметр | 1,5 | 60 В | 62 В | |
| вольтметр | 0,5 | 25 В | 27 В | |
| потенциометр | 0,5 | 450 | 455 | |
| Продолжение таблицы Б2 | ||||
| № варианта | Средство измерения | Относительная погрешность,% | Номинальное значение измеряемой величины | Показания средства измерения |
| потенциометр | 0,4 | 600 | 605 | |
| потенциометр | 1,0 | 750 | 745 | |
| потенциометр | 1,5 | 1100 | 1110 | |
| потенциометр | 0,2 | 500 | 506 | |
| омметр | 4,0 | 50 Ом | 55 Ом | |
| омметр | 5,0 | 250 Ом | 255 Ом | |
| омметр | 2,5 | 850 Ом | 855 Ом | |
| омметр | 2,0 | 1000 Ом | 1100 Ом | |
| омметр | 2,5 | 1750 Ом | 1800 Ом | |
| амперметр | 0,5 | 25 мА | 22 мА | |
| амперметр | 0,2 | 50 мА | 48 мА | |
| амперметр | 0,4 | 30 мА | 31 мА | |
| амперметр | 0,5 | 90 мА | 91 мА | |
| амперметр | 1,0 | 10 мА | 9 мА | |
| манометр | 2,0 | 40 кПа | 38 кПа | |
| манометр | 2,5 | 50 кПа | 55 кПа | |
| манометр | 1,5 | 60 кПа | 65 кПа | |
| манометр | 1,0 | 30 кПа | 32 кПа | |
| манометр | 2,5 | 65 кПа | 70 кПа |
Т а б л и ц а Б3- РГР №2, варианты задания №2, задача 3
| № варианта | Амперметр | Вольтметр | |||
| Iном, А | Диапазон измерений,А | Кл | Uном, В | Диапазон измерений, В | |
| 3,5 |  | 0,25 |  | ||
| 3,5 | | 0,5 | | ||
| 3,5 | | 0,3 | | ||
| 3,5 | | 0,4 | | ||
| 3,5 | | 1,0 | | ||
| 4,0 | | 0,25 | | ||
| 4,0 | | 0,5 | | ||
| 4,0 | | 0,3 | | ||
| 4,0 | | 0,4 | | ||
| 4,0 | | 1,0 | | ||
| 3,0 | | 0,25 | | ||
| 3,0 | | 0,5 | | ||
| 3,0 | | 0,3 | |
Продолжение таблицы Б3
| 3,0 | | 0,4 | | ||
| 3,0 | | 1,0 | | ||
| 2,5 | | 0,25 | | ||
| 2,5 | | 0,5 | | ||
| 2,5 | | 0,3 | | ||
| 2,5 | | 0,4 | | ||
| 2,5 | | 1,0 | | ||
| 2,0 | | 0,25 | | ||
| 2,0 | | 0,5 | | ||
| 2,0 | | 0,3 | | ||
| 2,0 | | 0,4 | | ||
| 2,0 | | 1,0 | |
Т а б л и ц а Б4- РГР №2, варианты задания №2, задача 4