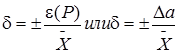Обработка результатов прямых равноточных измерений

При обработке результатов измерений необходимо найти оценки измеряемой величины и доверительный интервал, в котором находится истинное значение.

1. Определение точечных оценок закона распределения результата измерения.

1.1. Определяется среднее арифметическое значение 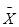измеряемой величины по формуле: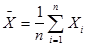

1.2. СКО результата измерения: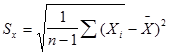

1.3. Определение СКО среднего арифметического: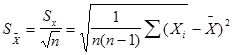

1.4. Исключение грубых погрешностей, по любому из рассмотренных критериев. В случае их обнаружения пересмотр точечных оценок.

2. Определение закона распределения.

2.1. Построение вариационного ряда, заключающегося в расположении результатов измерений в порядке возрастания.

2.2. Определение оптимального числа интервалов группирования. Вариационный ряд разбивается на оптимальное число m одинаковых интервалов группирования длинной h, определяемой по формуле: ;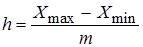

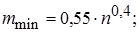
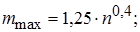
Искомое значение m должно находиться в пределах от m_min до m_max и быть нечетным. Установив границы интервалов, подсчитывают число результатов измерений n_k, попавших в каждый интервал.

2.3. По полученным значениям рассчитывают вероятности попадания результатов измерений (частости) в каждый из интервал группирования по формуле: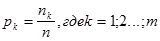

2.4. Произведенные расчеты позволяют построить гистограмму и полигон. Полигон представляет собой ломанную кривую, соединяющую середины верхних оснований каждого столбца гистограммы. Полигон более наглядно отражает форму кривой распределения.

2.5. Кумулятивная кривая - это график статистической функции распределения: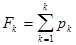

n_к р_к

1

Х_min Х_min+h Х Х_min Х_min+h Х

3. Оценка закона распределения. Проверка гипотезы о виде распределения экспериментальных данных.

Все предположения о характере распределения являются гипотезами, а не категорическими утверждениями. Следовательно, они должны быть подвергнуты статистической проверке с помощью так называемых критериев согласия. Критерии согласия, опираясь на установленный закон распределения, дают возмож­ность установить, когда расхождения между теоретическими и эм­пирическими (опытными) данными следует признать несущественными (слу­чайными), а когда — существенными (неслучайными). Критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой гипотезы о ха­рактере распределения в вариационном ряду и дать ответ, можно ли принять для данного вариационного ряда модель, выраженную некоторым теоретическим законом распределения. Существует ряд критериев согласия. Чаще других применяют критерии Пирсона, Романовского и Колмогорова. Рассмотрим их.

Критерий согласия Пирсона 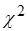(хи-квадрат) — один из основных критериев согласия. Критерий предложен английским математи­ком Карлом Пирсоном (1857—1936) для оценки случайности (су­щественности) расхождений между частотами эмпирического и теоретического распределений. Критерий Пирсона используется при числе экспериментальных данных n ³ 50.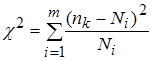

где m – число групп, на которые разбито эмпирическое распре­деление;

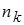– наблюдаемая частота признака в k-й группе;

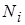– теоретическая частота, рассчитанная по предполагаемому распределению.

Вычисляют число наблюдений для каждого из интервалов теоретически соответствующий нормальному закону распределения, для этого от реальных середин интервалов Х_i0 переходят к нормированным по формуле: 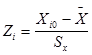(i = 1 . . . m)

Для каждого значения Z_i находят значение функции плотности вероятностей f(z_i):

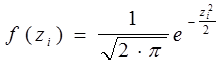(i = 1 . . . m)

3.3. По найденному значению f(z_i): определяется та часть N_i общего числа имеющихся наблюдений, которая теоретически должна быть в каждом из интервалов: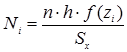

Для распределения 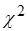составлены таблицы, где указано крити­ческое значение критерия согласия 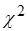для выбранного уровня зна­чимости a и данного числа степеней свободы v.

Уровень значимости a — вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В статистических исследованиях в зависимо­сти от важности и ответственности решаемых задач пользуются следующими тремя уровнями значимости:

1) а = 0,10, тогда Р = 0,90;

2) а = 0,05, тогда Р = 0,95;

3) а = 0,01, тогда Р = 0,99.

Например, вероятность 0,01 означает, что в одном случае из 100 может быть отвергнута правильная гипотеза. В экономических ис­следованиях считается практически приемлемой вероятность ошибки 0,05, т.е. в 5 случаях из 100 может быть отвергнута правильная гипотеза.

Кроме того, 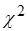критерий, определяемый по таблице, зависит и от числа степеней свободы. Число степеней свободы v определяется как число групп в ряду распределения m минус число связей z.

v = k — z

Под числом связей обычно понимается число показателей эмпирического (вариационного) ряда, использованных при исчислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты ( )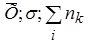

Так, например, в случае выравнивания по кривой нормального распределения имеется три связи:

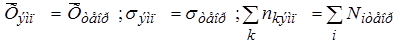
Поэтому при выравнивании по кривой нормального распределе­ния число степеней свободы определяется как v = k — 3, где k — число групп в ряду.

Для оценки существенности расчетное значение 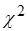сравнивается с табличным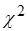

При полном совпадении теоретического и эмпирического рас­пределений 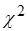= 0, в противном случае 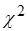>0. Если 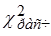> 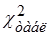при заданном уровне значимости a и числе степеней свободы v гипотезу о несущественности (случайности) расхождений откло­няем.

В случае если 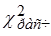£ 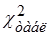заключаем, что эмпирический ряд хорошо согласуется с гипотезой о предполагаемом распределении и с вероятностью (1 — a) можно утверждать, что расхождение меж­ду теоретическими и эмпирическими частотами случайно.

Используя критерий согласия 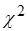, необходимо соблюдать следу­ющие условия:

1) объем исследуемой совокупности должен быть достаточно большим (N > 50), при этом частота или численность каждой группы должна быть не менее 5. Если это условие нарушается, необходимо предварительно объединить маленькие частоты;

2) эмпирическое распределение должно состоять из данных, полученных в результате случайного отбора, т.е. они должны быть независимыми.

Критерий Романовского с основан на использовании критерия 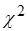Пирсона, т.е. уже найденных значений 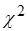, и числа степеней сво­боды v:

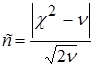
Он весьма удобен при отсутствии таблиц для .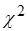

Если с < 3, то расхождения между теоретическим и эмпириче­ским распределением случайны, если же с > 3, то не случайны и, соответственно, теоретическое распределение не может служить моделью для изучаемого эмпирического распределения (вариационного ряда).

Критерий Колмогорова l основан на определении максимально­го расхождения между накопленными частотами или частостями (суммарными частотами) эмпирических и теоретических распределений:

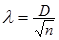или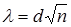

где D и d соответственно максимальная разность между накоп­ленными (куммулятивными) частотами ( 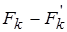) и между частотами попадания ( 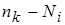) эмпирического и теоретического рядов распределений;

n - число единиц в совокупности.

Рассчитав значение l., по таблице P(l) оп­ределяют вероятность, с которой можно утверждать, что отклоне­ния эмпирических частот от теоретических случайны. Вероятность P(l) может изменяться от 0 до 1. При P(l) = 1 происходит полное совпадение частот, при P(l) = 0 — полное расхождение. Если X принимает значения до 0,3, то P(l) = 1.

Основное условие для использования критерия Колмогорова — достаточно большое число наблюдений.

При числе экспериментальных данных n ³ 50 для проверки критерия согласования теоретического распределения с практическим чаще всего используют критерий Пирсона (c²). Идея этого метода состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенной на основе нормального распределения.

3.1. Вычисляют число наблюдений для каждого из интервалов теоретически соответствующий нормальному закону распределения, для этого от реальных середин интервалов Х_i0 переходят к нормированным по формуле: 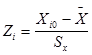(i = 1 . . . m)

3.2. Для каждого значения Z_i находят значение функции плотности вероятностей f(z_i):

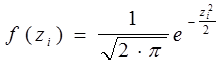(i = 1 . . . m)

3.3. По найденному значению f(z_i): определяется та часть N_i общего числа имеющихся наблюдений, которая теоретически должна быть в каждом из интервалов: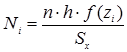

3.4. Вычисление величиныc².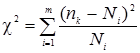

3.5. Если в какой-то из интервалов, теоретически попадает меньше 5 наблюдений, то в обеих гистограммах его соединяют с соседним интервалом. После этого определяют число степеней свободы:

v = m - 1 - r, где m - общее число интервалов; r - число определяемых по статистике параметров, необходимых для совмещения модели и гистограммы (r = 2).

3.6. Выбирают (по таблице) уровень значимости q, который должен быть небольшим. По уровню значимости и числу степеней свободы находят границу критической области c²_q (табл.). Если c²_q > c², то гипотеза о нормальном значении принимается.

4. Определение доверительной границы погрешности результата измерений.

4.1. Расчет доверительных границ e погрешности измерения. При нормальном законе распределения, доверительные границы вычисляются по формуле: 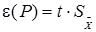, где t - коэффициент Стьюдента.

4.2. При нормальном законе распределения результатов измерений истинное значение измеряемой величины Х, с доверительной вероятностью Р (Р=0,95), находится в пределах: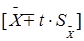

4.3. Расчет доверительных границ суммарной неисключенной систематической составляющей погрешности измерения. 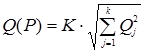, где К - коэффициент соответствующей выбранной доверительной вероятности (при Р = 0,95 К = 1,1). В данном случае неисключенная систематическая погрешность измерения обусловлена одной составляющей Q_j = 0,004 мкм.

4.4. Вычислим соотношение 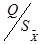. Если полученное значение лежит в пределах 0,8 ¸ 8,0, то ни одной из составляющих погрешности измерения пренебречь нельзя, следовательно, погрешность результата будет содержать как случайную так и не случайную составляющие погрешности.

4.5. Доверительные границы общей погрешности измерения:

; ;

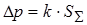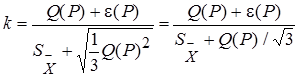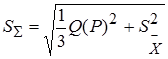
где к - коэффициент, S_å - суммарное среднее квадратическое отклонение результата измерения.

4.6. Следовательно, результат измерений можно записать в виде: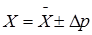

4.7. Если величина e(Р) окажется сравнимой с абсолютной погрешностью СИ (0,004), то в качестве доверительного интервала следует взять величину: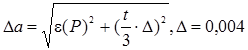

4.8. Окончательный результат записывается в виде: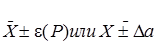

Относительная погрешность результата серии измерений выразится как: