Лекция 4. 2.6. Неразветвлённая цепь переменного тока с активным сопротивлением, индуктивностью и ёмкостью

2.6. Неразветвлённая цепь переменного тока с активным сопротивлением, индуктивностью и ёмкостью. Резонанс напряжений

Рассмотрим неразветвлённую электрическую цепь (рис. 2.21).

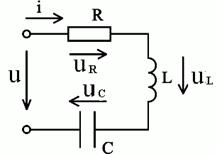
Рис.2.21. Схема неразветвлённой электрической цепи с активным сопротивлением, индуктивностью и ёмкостью

Пусть 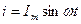, тогда .

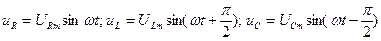Построим векторную диаграмму при условии, что действующие значения напряжений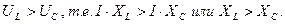

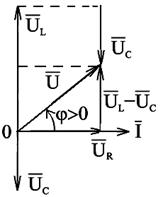
Рис.2.22. Векторная диаграмма действующих значений тока и напряжений для

цепи переменного тока с активным сопротивлением, индуктивностью и

ёмкостью, в которой ( )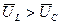

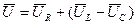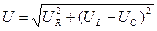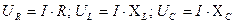Из векторной диаграммы (рис.2.22) следует: , откуда . Но , следовательно 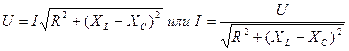. Введя обозначение полного сопротивления цепи 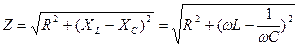, найдем:

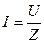. (2.22)

Разность между индуктивным и емкостным сопротивлениями называют реактивным сопротивлением цепи X = XL - XC. Учитывая это, получим треугольник сопротивлений для цепи с R, L и C (рис. 2.23).

При XL > XC реактивное сопротивление положительно и угол 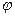> 0.

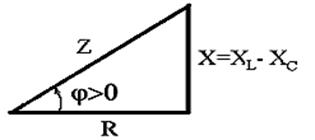
Рис.2.23. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью ( )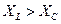

При XL > XC реактивное сопротивление положительно и угол 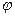> 0. Аналогично можно построить векторную диаграмму для действующих значений напряжений 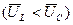(рис. 2.24) и треугольник сопротивлений 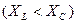(рис. 2.25).

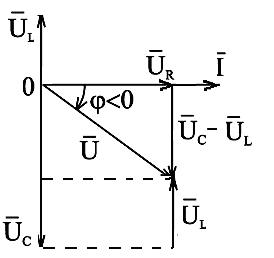
Рис.2.24. Векторная диаграмма действующих значений тока и напряжений ( 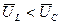) цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью

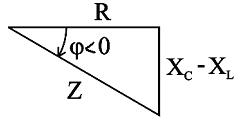
Рис.2.25. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью ( )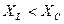

При XL < XC реактивное сопротивление X отрицательно и угол 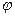< 0. Если UL = UC и XL = XC , то векторную диаграмму можно представить в виде рис. 2.26, а зависимость тока от частоты в виде рис.2.27.

В этом случае наступает резонанс напряжений, когда ток в цепи совпадает по фазе с напряжением источника. При этом угол 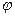= 0, так как реактивное сопротивление равно нулю.

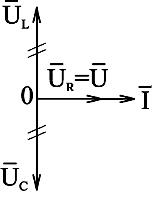
Рис.2.26. Векторная диаграмма резонанса напряжений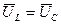

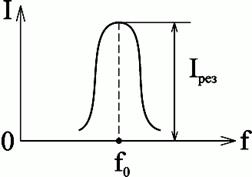
Рис.2.27. Зависимость тока от частоты питающей сети для резонанса напряжений

При резонансе напряжений частота источника равна собственной частоте колебаний LC-контура. Если 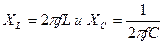, где f - частота источника питания, то можно записать 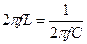. Решив это уравнение относительно f, получим:

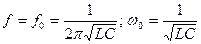. (2.23)

На основании рис.2.26, 2.27 следует, что признаками резонанса напряжений являются:

а) полное сопротивление цепи равно активному сопротивлению Z = R;

б) ток в цепи совпадает по фазе с напряжением источника и имеет максимальное значение;

в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности превышает по величине напряжение источника;

г) коэффициент мощности cos 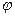= 1.

На рис.2.28 изображены примерные функциональные зависимости индуктивных и емкостных напряжений, тока и коэффициента мощности в зависимости от изменения ёмкости конденсатора, где Cp - резонансная ёмкость.

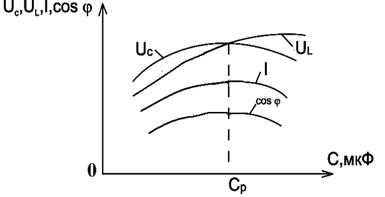
Рис.2.28. Примерное изображение зависимостей UL, UC, 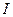, cos 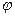от изменения ёмкости конденсатора C

Количественная оценка соотношения энергий источника, катушки индуктивности и конденсатора при резонансе напряжений характеризуется добротностью контура:

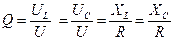. (2.24)

Величину 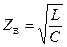при резонансе называют волновым сопротивлением контура.