Обработка результатов прямых равноточных измерений

(Метод максимального правдоподобия)

Прямыми измерениями называются измерения, при которых искомое значение величины находят непосредственно из опытных данных.

Равноточными (равнорассеянными) называются прямые независимые измерения постоянной величины, результаты которых могут рассматриваться как случайные, распределенные по одному и тому же закону.

Обычно считают, что распределение подчиняется нормальному закону, хотя это условие вовсе необязательное.

В неисправленные результаты наблюдения вводят поправки с целью устранения систематических погрешностей. Таким образом, получают исправленный результат наблюдения, не содержащий систематических погрешностей, с математическим ожиданием погрешности 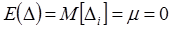, и дисперсией погрешности 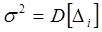одинаковой для всех измерений (отсюда равноточность измерений).

Плотность распределения результатов каждого из измерений при нормальном законе распределения имеет вид:

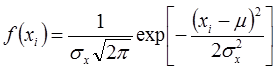
Из данных условий найдем наилучшую оценку .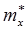

Для этого применим метод максимального правдоподобия, который является одним из основных методов построения оценок неизвестного параметра в статистической теории оценивания.

Поскольку измерения независимы, то плотность распределения системы измерений 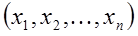будет равна:

.

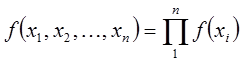Функция правдоподобия имеет вид:

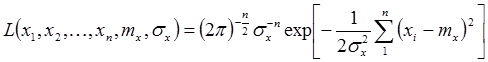
Метод максимального правдоподобия рекомендует принять в качестве оценк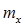и и 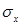статистику 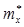, определяемую соотношением :

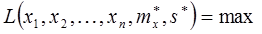
Примечание: Статистикой называется функция от результата наблюдений, являющаяся случайной величиной. Примеры: оценка математического ожидания 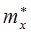, оценка дисперсии 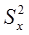, оценка СКО .

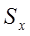Для нахождения максимума решают уравнения правдоподобия.

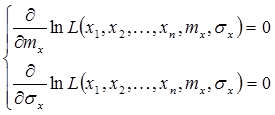
Для нашего случая, подставляя в уравнения функцию правдоподобия, эти уравнения примут вид:

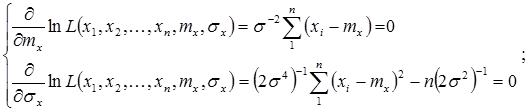
Решая, получим:

,

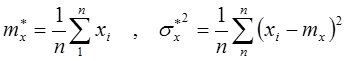или

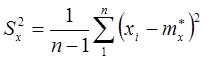
Примечание: Для наиболее часто встречающегося на практике нормального распределения случайных погрешностей оценки метода максимального правдоподобия имеют особые обозначения.

Вторая производная функции правдоподобия по математическому ожиданию равна:

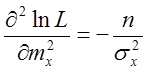, откуда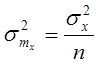

или , .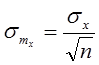

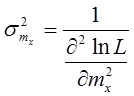Оценка СКО ряда наблюдений:

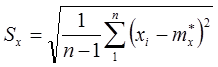
Оценка СКО среднего арифметического (результата измерений):

.

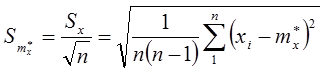Обратим внимание на формулы. Оценки стандартных отклонений СКО S в ряду наблюдений отличаются от «точных» стандартных отклонений σ , что вызвано использованием арифметического среднего вместо математического ожидания.