Структурные средние. Мода, медиана, квартиль, дециль, проценты

Модой в статистике назыв. наиболее часто встречающиеся значения признака либо варианта совокупности. В дискретном вариационном ряду мода – это вариант, обладающий наибольшей частотой.

Для опр-ния моды в интервальном вариационном ряду сначала отыскивается модальный интервал (т.е. интервал, обладающий наибольшей частотой), а в рядах с неравными интервалами – по наибольшей плотности распределения.

Формула моды для интервальных вариационных рядов с равными интервалами:

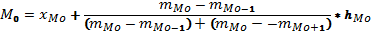
Медиана – это значение признака у той единицы совокупности, кот. делит упорядоченный, ранжированный вариационный ряд пополам, т.е. половина совокупности имеет значение меньше медианы, а другое – больше.В дискретном вариационном ряду медиана – это интервал, кот. находится в центре ранжированного ряда.ахождение медианы в интервальном вариационном ряду требует предварительного нахождения медианного интервала.Таким интервалом будет тот, накопленная (коммулитативная) частота кот. равна или превышает полу сумму частот ряда распределения.После опр-ния медианного интервала, медиана вычисляется путём линейной интерпретации, т.е. по формуле: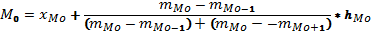

Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 частей.

Расчет этих показателей в вариационном ряду аналогичен расчету медианы и начинается с нахождения порядкового номера соотв. варианта и опр-ния по накопленной частоте того интервала, в кот. этот вариант находится. Затем с помощью линейной интерпретации, т.е. по формуле.

Квартиль находится по формуле:

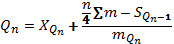
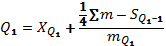
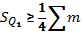
децили – значения признака, которые ранжированный ряд делят на 10 равных частей. Расчеты ведутся аналогично расчетам квартилей:

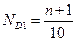и так далее до 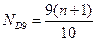, где n – общее число единиц в совокупности

Численное значение определяется по формуле:

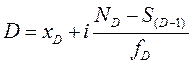
где x_D – нижняя граница интервала, в котором находится дециль

N_D – место децили

S_(D-1) – накопленная частота интервала, предшествующего тому, где находится дециль

f_D – частота интервала, в котором находится дециль

15. Абсолютные и средние показатели вариации размах среднее линейное отклонение. Вариационными называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности непостоянны, более или менее различаются между собой.

Вариация - колеблемость, изменяемость величины признака у единиц совокупности. Отдельные числовые значения признака, встречающиеся в изу­чаемой совокупности, называют вариантами значений. Недостаточность средней величины для полной характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака.

Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним.

Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них - размах вариации.

Размах вариации - это разность между наибольшим ( 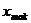) и наименьшим ( 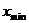) значениями вариантов.

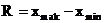
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.

Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.

Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:

.

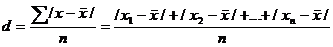Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:

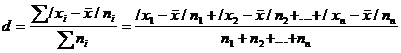
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонени Этот показатель вычисляется как разность между наибольшим и наименьшим значениями варьирующего признака:

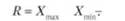
Он показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое (А"т(п) и самое большое значение признака (Хтах). Например, различие между максимальной и минимальной пенсией разных групп населения, уровнем дохода различных категорий работающих или нормами выработки у рабочих определенной специальности или квалификации.

16 Дисперсия…

Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается 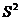. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
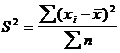— дисперсия невзвешенная (простая);
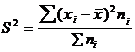— дисперсия взвешенная.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S:
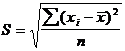— среднее квадратическое отклонение невзвешенное;
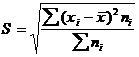— среднее квадратическое отклонение взвешенное.

Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.

Вычислению среднего квадратического отклонения предшествует расчет дисперсии.

Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить дискретное значение признака, а далее применить тот же метод, что изложен выше.

Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.

Свойства дисперсии.

1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.

2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.

3. Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в 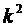раз, а среднее квадратическое отклонение - в к раз.

4. Дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.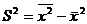

Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.