Постановка задачи оптимального резервирования

Информационные системы состоят из отдельных элементов. Эти элементы с течением времени отказывают и заменяются резервными. Снятые с эксплуатации элементы подвергаются ремонту.

Модель должна определять оптимальный уровень резервных элементов каждого типа. По условию задачи требуется, чтобы система функционировала с максимальной надежностью. Если какой-нибудь элемент отказывает, то его заменяют запасным из числа резервных. Отказавший элемент сразу начинают ремонтировать. В системе непрерывно должно функционировать 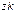элементов 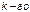типа, причем в запасе должно иметься 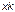элементов того же 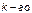типа .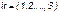

Сущность задачи заключается в оптимальном распределении стоимостных или каких-либо других ресурсов 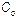, выделенных на приобретение резервных единиц.

Рассматриваемая система считается отказавшей, если в момент отказа работающего элемента 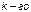типа все 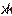запасных элементов того же типа находятся в ремонте. Таким образом, надо найти количество резервных элементов 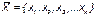так, чтобы вероятность нехватки резервных элементов была минимальной.

Введем обозначения:

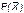- показатель надежности всей системы (вероятность безотказной работы системы);

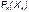- вероятность безотказной работы 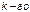элемента.

Так как модель соединений элементов с точки зрения надежности представляется как последовательное соединение элементов, то справедлива формула

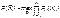
Можно сформулировать задачу на минимум: необходимо найти минимум риска нехватки элементов

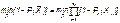
На все элементы есть ограничения (вес, цена, объем и т.д.). Но мы будем пользоваться только стоимостным ограничением, как, пожалуй, наиболее часто встречающимся, хотя задача решается и для нескольких ограничений.

,

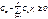где 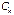- стоимость одного элемента k-го типа.

35 Прежде всего для решения задачи оптимального резервирования используется метод неопределенных множеств Лагранжа:

Необходимо найти:

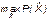
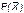- показатель надежности всей системы (вероятность безотказной работы системы);

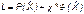
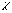— неопределенный множитель Лагранжа; 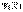— ограничение.

Решив систему уравнений, можно найти необходимое количество резервных элементов.

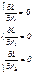
Метод не дает однозначного решения: аргументы будут нецелочисленными (надо округлять), ограничения заданы в виде строгого равенства, а надо больше или равно.

Для устранения указанных недостатков решения задачи оптимального резервирования используется градиентный метод.

Экстремум функции ищется из начальной точки по направлению градиента по шагам. Для оптимального резервирования на первом шаге отыскивается тот элемент системы, который дает наибольший прирост показателя надежности, на втором - элемент, у которого имеется максимальный прирост показателя надежности, включая уже зарезервированный, до тех пор, пока не выполниться ограничение (по стоимости). Метод называется покоординатным спуском, который является одним из самых простых методов поиска экстремума функции многих переменных (рис. 4.2).

В литературе говориться, что данный метод может «застревать», когда линии уровня сильно вытянуты (см. рис. 4.2 б), т.е. пробные шаги во всех направлениях не приводят к уменьшению значения целевой функции, и процесс вычисления прерывается вдали от точки минимума.

Рис. 4.2 Поиск минимума функции двух переменных
методом покоординатного спуска

Но так как надо минимизировать функцию надежности системы

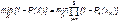
которая при всегда будет уменьшаться при увеличении количества резервных элементов, можно не усложнять алгоритм покоординатного спуска, например методом предложенным Хуком и Дживсом.

36 Для решения задачи оптимального резервирования также используется метод динамического программирования.

Рассмотрим алгоритм решения поставленной задачи методом динамического программирования. В основе метода лежит пошаговый процесс, на каждом шаге строится доминирующая последовательность

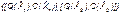
где переход в состояние с более высокой надежностью (или более низкой вероятностью отказа Q) происходит с минимальными затратами по стоимости C,

здесь 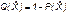- риск нехватки резервных элементов.

Доминирующая последовательность строится по следующему правилу

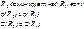
Алгоритм построения доминирующей последовательности состоит из шагов, на каждом из которых строится следующая таблица.

Рассматриваем две подсистемы из 1-го и 2-го типа элементов. Характеристики элементов 1-го типа записываются в заголовках столбцов, а характеристики 2-го типа - в заголовках строк. На пересечении каждой строки и каждого столбца записываются суммы стоимостей C и вероятностей нехватки элементов q. (табл. 1).

Таблица 1.

	x1
x1=0 q1 c1	x1=1 q12 2c1	x1=2 q13 3c1
x2	x2=0 q2 c2	q1+q2 c1+c2	q12+q2 2c1+c2	q13+q2 3c1+c2
x2=1 q22 2c2	q1+q22 c1+2c2	q12+q22 2c1+2c2	q13+q22 3c1+2c2
x2=2 q32 3c2	q1+q23 c1+3c2	q12+q23 2c1+3c2	q13+q23 3c1+3c2

Вначале проводим анализ элементов таблицы по ограничениям . Вычеркиваем те элементы, которые имеют значение стоимости большее, чем ограничение по стоимости Co и, чем ограничение по вероятности нехватки элементов Qo.

Делаем анализ на доминирование: рассматриваются оставшиеся клетки и сравниваем последовательно со всеми элементами (клетками). Если для каких-то двух векторов выполняется условие строгого доминирования, то т худший вычеркивается.

Вектор X₁ доминирует над вектором X₂, если вероятность нехватки элементов P(X₁) ³ P(X₂), а стоимость С(X₁) £ С(X₂) или вероятность нехватки элементов Q(X₁) £ Q(X₂) и стоимость С(X₁) £ С(X₂). Вектор X₁ строго доминирует над вектором X₂, если одно из перечисленных неравенств будет строгим.

Все оставшиеся элементы переносим в заголовки столбцов, а в качестве заголовков строк будут выступать характеристики элементов третьего типа.

Всего будет S-1 таблица, на последнем шаге вычислений ищется оптимальный вектор, у которого и будет минимальная вероятность отсутствия резервных элементов.

Надежность ПО ИС

ИС является сложной техн. системой, которая работает под управлением сложных программных комплексов. При разработке программных комплексов на этапе проектирования возникают ошибки, искажения. Эти ошибки и искажения влияют на надежность ПО. Поэтому необходимо производить расчеты показателей надежности ПО. Они несколько отличаются от расчетов надежности ТС и изделий. При оценке надежности ПО необходимо решить сл. задачи:

1. Определение показателей, которые используются при расчете надежности ПО. Вводятся понятия функцион. отказа, надежности, функциональной надежности – ошибки в самом ПО. Показатели конструктивной надежности – надежность ТС на которых вып-ся ПО.

2. Формирование системы показателей ПО. Используются показатели безотказности и ремонтопригодности.

3. Задача анализа факторов, от которых зависит надежность ПО. Определяется путем исследования искажений и сбоев ПО.

4. Методы разработки комплексов ПС, заданных характеристиками надежности.

5. Прогнозирование показателей надежности разрабатываемых ПС.