Постановка задачи оптимального проектирования

Рассмотрим задачу проектирования некоторого технического устройства (объекта). Ее решение можно условно разделить на два этапа:

Шаг 1. Определить конструкцию (структуру) устройства и построить его математическую, алгоритмическую и программную модель, то есть решить прямую задачу вычислительного эксперимента. В дальнейшем будем предполагать, что построена детерминированная модель некоторого объекта (устройства), которая связывает векторы входных 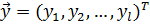и выходных 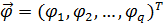параметров с помощью известного математического оператора :

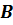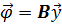. (1.1)

Вектор входных параметров 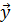можно разделить на две компоненты: вектор независимых внутренних параметров 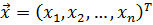и вектор параметров внешних воздействий на объект :

.

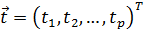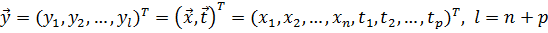Шаг 2. Сконструировать оптимальное устройство, у которого один или несколько выходных параметров 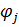наиболее близки к их оптимальным (наилучшим) значениям 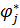: решить задачу оптимального проектирования.

1.1 Параметрическая и структурная оптимизация. Для того, чтобы приблизить выходные параметры к оптимальным значениям можно использовать два способа. Построив модель устройства (Шаг 1), можно найти такие численные значения независимых входных параметров (варьируемых параметров) 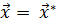, которые при заданном операторе B обеспечивают наилучшее приближение выходных параметров 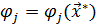к оптимальным значениям 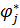(Шаг 2). В этом случае задача, решаемая на Шаге 2, называется задачей параметрической оптимизации. Если ее решение невозможно или не дает приемлемых результатов, можно попытаться улучшить выходные параметры за счет изменения конструкции (структуры) устройства и вернуться к Шагу 1. Это означает изменение математической модели, то есть оператора B. Такая оптимизация называется структурной.

Задачи структурной оптимизации являются существенно более сложными и плохо формализуются для решения на ЭВМ. К тому же, способы их решения практически полностью зависят от типа проектируемого устройства: общих методов не существует. Напротив, задачи параметрической оптимизации относительно легко формализуются и допускают общую математическую формулировку. Для решения этих задач разработан специальный математический аппарат – методы оптимизации.

Далее рассмотрим постановки и методы решения задач параметрической оптимизации.

1.2 Целевые функции. Рассмотрим вначале задачу однокритериальной параметрической оптимизации. Наличие одного критерия оптимальности означает, что оптимизация выполняется относительно значения только выходного параметра.

В простейшем случае задача однокритериальной оптимизации заключается в том, чтобы при известных значениях параметров внешних воздействий 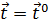приблизить к заданному значению 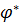значение одного выходного параметра :

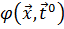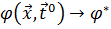(1.2)

Решая задачу параметрической оптимизации, нужно получить такое оптимальное значение 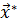, которое наилучшим образом приблизит один выходной параметр 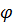к оптимальному значению 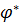. При этом отнюдь не обязательно, что удастся добиться точного совпадения достигнутого значения выходного параметра 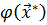и оптимального значения 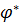. Например, оптимизируемым выходным параметром может быть стоимость устройства, а оптимальным значением – недостижимое .

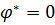Для того, чтобы формализовать и решить численно на ЭВМ задачу (1.2), ее сводят к математической задаче нахождения минимума некоторой скалярной функции 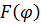. Так как мы рассматриваем детерминированные модели, для которых определена функциональная зависимость 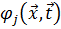, можно сразу рассматривать функцию 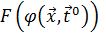как функцию внутренних параметров 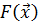, вычисляемую при заданных значениях параметров внешних воздействий 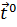. Такую функцию называют целевой функцией. В частности, решение задачи (1.3) можно свести к математической задаче нахождения минимума функции n переменных 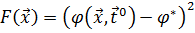или другой, достигающей минимума в точке 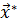, в которой отклонение 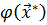от оптимального значения 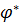является наименьшим.

В более сложном случае устройство должно иметь оптимальную выходную характеристику 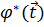на некотором множестве значений вектора параметров внешних воздействий на объект T. Обычно это множество представляет собой некоторый диапазон изменения 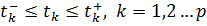. В этом случае получаем задачу вида:

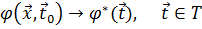. (1.3)

Для решения задачи (1.3) можно одним из нескольких возможных способов ввести понятие расстояния 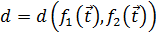между функциями 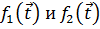: на множестве T. Функционал d, определяющий расстояние между функциями, должен обладать следующими свойствами:

1.

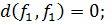
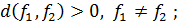
2. ;

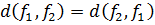3.

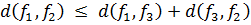
Например, для минимизации среднеквадратичного отклонения выходной характеристики 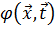от оптимальной 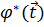, можно ввести расстояние между этими функциями и соответствующую целевую функцию следующим образом:

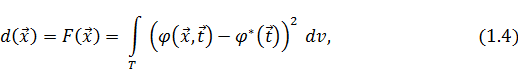
где интегрирование ведется по всей области значений T, а dv – элемент объема этого множества. Для численного вычисления на ЭВМ такой интегральной целевой функции можно на множестве T случайным образом выбрать N точек 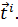Тогда с точностью до постоянного множителя, зависящего от T, значение целевой функции (1.4) аппроксимируется функцией вида:

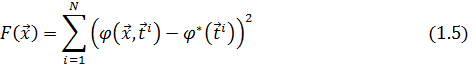
Зная вид оптимальной характеристики, часто вместо случайного выбора точек 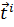используют детерминированную регулярную или нерегулярную сетку из таких точек, покрывающую T. Наконец, для того, чтобы более критичные с точки зрения разработчика участки выходной характеристики вносили более значительный вклад в значение целевой функции, можно задать весовую функцию 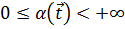, принимающую большие значения в более значимых областях множества T:

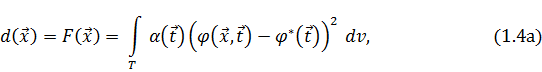
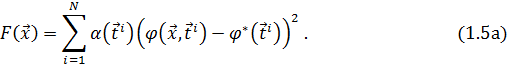
Целевые функции (1.4-1.5) имеют недостаток: существенные отклонения выходной характеристики в очень узкой области изменения параметров внешних воздействий (выбросы) незначительно увеличивают значения этих целевых функций. Это может привести к тому, что устройство с очень большими, но очень узкими выбросами выходной характеристики окажется оптимальным, что не всегда приемлемо. Чтобы этого избежать, можно использовать минимаксную целевую функцию и минимизировать

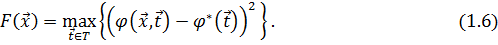
Для вычисления на ЭВМ, как и ранее, покроем T сеткой точек 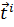и будем вычислять

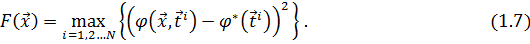
Аналогично (1.5а,1.6а) введем в (1.7,1.8) весовую функцию 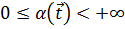, принимающую большие значения в более значимых областях множества T:

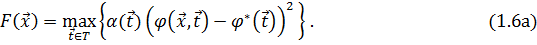
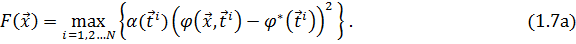
Еще раз подчеркнем, что целевая функция никогда не зависит от параметров внешних воздействий. Мы не можем изменять их, стремясь оптимизировать устройство. Например, проектируемый полупроводниковый усилитель должен оставаться работоспособным в некотором диапазоне амплитуд 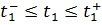и частот 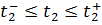входного сигнала. В этом случае амплитуда 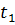и частота 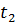подаваемого сигнала являются параметрами внешних воздействий. Значения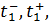 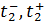, определяющие множество T, войдут в структуру целевой функции в качестве констант. Таким образом, задача однокритериальной параметрической оптимизации сводится к задаче минимизации скалярной целевой функции, зависящей от n независимых входных параметров :

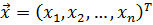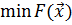(1.8)

Минимум целевой функции достигается в точке 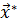, в которой оптимизируемый выходной параметр 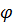наиболее близок к требуемому значению 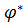. Если же мы имеем дело с заданной оптимальной характеристикой 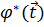, то выбор целевой функции (например, интегральной или минимаксной) задает критерий близости заданной характеристики и характеристики 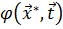, полученной при .

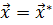По сути, построив целевую функцию F, мы получили способ сравнения альтернативных конфигураций проектируемого устройства, которые соответствуют различным значениям вектора независимых входных параметров: чем меньше значение этой функции, тем лучше устройство.

1.3 Ограничения. В процессе параметрической оптимизации, как правило, значения варьируемых параметров 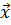можно изменять в определенных пределах. Такие ограничения связаны либо с физической природой параметра (например, емкость конденсатора ограничена снизу: она не может быть отрицательной) или с требованиями конструктивного исполнения (емкость того же конденсатора ограничена и сверху: теоретически возможно создать конденсатор емкостью 1 Фарада, но вряд ли его габариты окажутся приемлемыми). В общем случае

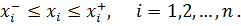(1.9)

Эти ограничения называют явными или прямыми. Их можно свести к системе односторонних неравенств:

(1.10)

Разумеется, ограничения могут быть более сложным и накладываться не на значения самих варьируемых параметров, а на значения, которые принимают некоторые известные функции этих параметров. 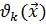. Требование, чтобы значения этих функций оставались в требуемом диапазоне значений от 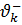до 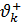можно сформулировать в виде ограничений – двойных неравенств:

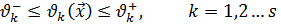(1.11)

Более жесткие требования точного равенства некоторых параметров устройства 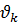соответствующим номинальным значениям 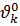можно записать в виде ограничений – равенств:

(1.12)

Последние можно свести к двойным неравенствам вида:

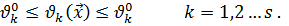(1.13)

В свою очередь, двойные неравенства (1.11,1.13) сведем к системам односторонних неравенств:

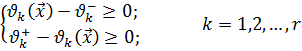(1.14)

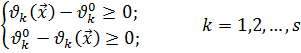(1.15)

Объединяя (1.10,1.14,1.15), получим вектор функций-ограничений 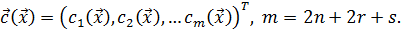Для каждой компоненты этого вектора должно выполняться неравенство:

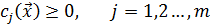(1.16)

В дальнейшем систему неравенств (1.17) будем записывать более кратко:

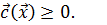(1.17)

Выражения (1.8) и (1.17) вместе составляют математическую модель задачи однокритериальной параметрической оптимизации:

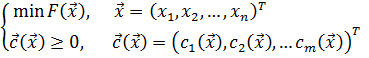(1.18)

1.4 Многокритериальная оптимизация. Как правило, в реальных задачах оптимизировать нужно значение не одного выходного параметра, а сразу нескольких. Такие задачи называются многокритериальными. Для оптимизации по каждому из нескольких выходных параметров 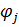можно предложить соответствующую целевую функцию 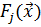так, как это описано в разделе 1.2. Проблема заключается в том, что, как правило, критерии оптимальности противоречивы, то есть в точке минимума одной целевой функции, значения других функций могут быть весьма далеки от минимальных. Например, для самого простого случая одного варьируемого параметра 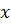и двух целевых функци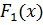й и 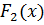эту проблему можно проиллюстрировать рис. 1.1.

Формально задачу многокритериальной параметрической оптимизации можно записать в виде:

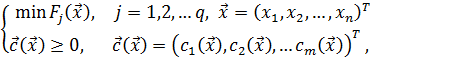(1.19)

однако, в общем случае, однозначное решение этой задачи отсутствует.

Для решения задачи (1.19), прежде всего, можно попытаться разделить область допустимых значений варьируемых параметров D, определяемую неравенствами 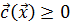, на две: область согласия 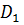и область компромиссов 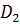. Для любой точки в области согласия 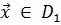должен существовать такой вектор 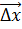, что для всех целевых функций 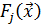выполняется неравенство 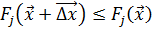, а хотя бы для одной из этих функций 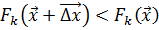. Таким образом, в области согласия имеется такое перемещение 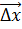, при котором все целевые функции ведут себя согласованно, одновременно уменьшаясь. Очевидно, решение задачи (1.19) не может лежать в области согласия 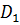, так как для любой точки 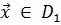, можно указать точку 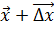, в которой значения всех целевых функций меньше, чем в .

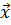Напротив, в области компромиссов 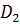, которую составляют точки области допустимых значений 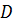, не принадлежащие области согласия 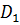: 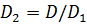, целевые функции ведут себя несогласованно. Это значит, что нельзя уменьшить значение одной из целевых функций, не увеличив значение хотя бы одной другой. Таким образом, решениями задачи (1.20) являются значения варьируемых параметров 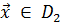. Эти точки в литературе также называют эффективными или неулучшаемыми точками, а 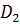- множеством решений, оптимальных по Парето.

Для того, чтобы из множества решений, оптимальных по Парето, выделить одно решение, устраивающее разработчика, последний должен выполнить ранжирование по значимости заданных критериев оптимальности и соответствующих им целевых функций 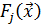. Для этого будем рассматривать вектор целевых функций: 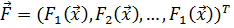. Предположим, что, сравнивая два вектора целевых функци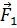й и 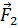, соответствующих двум различным векторам варьируемых параметров, разработчик может определить, какой из них соответствует лучшему устройству, то есть является более предпочтительным. Введем теперь скалярную функцию (функцию полезности) 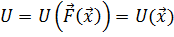следующим образом: 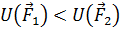тогда и только тогда, когда вектор 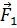более предпочтителен чем 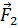. Тогда оптимальное решение можно найти, минимизируя скалярную функцию 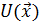при соответствующих ограничениях:

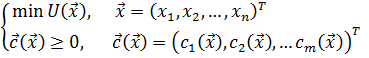(1.20)

По сути, это означает свертывание векторного критерия оптимальности 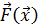(сведение его к скалярной функции 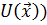. Решение задачи многокритериальной параметрической оптимизации сводится к минимизации скалярной функции, аналогично модели задачи однокритериальной оптимизации (1.18). Далее рассмотрим основные способы свертывания векторных критериев оптимальности.

Аддитивный критерий оптимальности получаем, выполняя суммирование частных критериев 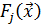с весовыми коэффициентами :

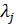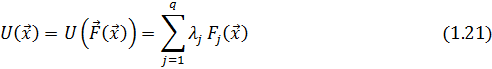
Весовые коэффициенты в (1.21) выполняют две функции. Во-первых, с их помощью частные критерии можно сделать однородными и соизмеримыми (то есть количественно сравнимыми в одной размерности). Далее, варьируя значения 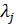, можно изменять относительную важность одних критериев по отношению к другим. Недостатком аддитивного способа свертывания векторного критерия оптимальности является то, что решение, полученное путем минимизации функции (1.21) может оказаться неприемлемым по некоторым частным критериям. Большие значения соответствующих целевых функций могут быть скомпенсированы очень малыми значениями остальных.

Минимаксный критерий оптимальности позволяет получить решение, свободное от выбросов значений отдельных целевых функций. Минимизируется функция полезности, имеющая вид:

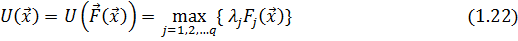
Здесь весовые коэффициенты 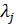играют ту же роль, что и в (1.21).

Метод выделения главного критерия предполагает, что в качестве функции полезности выбирается одна из целевых функций, соответствующая наиболее значимому критерию оптимальности:

На значения остальных целевых функций налагаются ограничения вида:

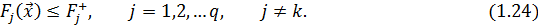
Нетрудно видеть, что результатом минимизации функции полезности, введенной любым из перечисленных способов, всегда будет вектор варьируемых параметров, принадлежащий множеству решений, оптимальных по Парето.