Ошибки наблюдения – расхождения между данными наблюдения и действительными значениями показателей

Предметом – совокупности ( множество однокачественных варирующих явлений. 3основн. Категории: 1) множество явл. 2) множество явл., обьедененных общим кач-вом 3) множество варирующих явлений. Совокупность является однородной если один или несколько изуч. Признаков ее обьектов являются общими для всех ед.. Сов-ть в кот. Входят явл. Разного типа, считается разнородной. Единицы сов-ти – первичный элемент стат. Сов-ти, является носителем признаков, подлежащих регистрации и основой ведущегося при обследовании счета. Ед. сов-ти одладает определенными свойствами, качествами кот. Принято называть признаками. Классификация признаков: 1)по ур-ню измерения(качественные.) – альтернативные, кот. Могут принимать 2 знач. –наменальные, по кот нельзя упорядочивать ед. -порядковые,, те. Кот. Могут . 2)по отношению к ед. сов-ти – первичные, характериз. Ед. сов-ти в целом – вторичные, не измеряются непосредсвенно а рассчитываются. 3)в зависимости от времени – интервальные, если зависит от интервала значение признака – моментные, если знач.может быть определенно по сост. На любой момент времени.

Методы: 1) стат. Наблюдение – сбор первичного стат. Материала, регисьтрация всех существенных факторов. 2) обобщение – группировка и сводка. 3) метод обобщающих показателей – позволяет характеризовать изучаемые явления и процессы, а так же выявлять взаимосвязи и масштабы явлений.

2 Основные задачи статистики

3 Основные стадии статистического исследования.

Исходя из изменений управления, роли и места предприятий, фирмы, межрегиональных отношений и отношений внешним миром, основными статистики на современном ее этапе являются: 1) всестороннее исследование происходящих в обществе глубоких преобразований экономических и социальных процессов на основе научно обоснованной системы показателей; 2) обобщение и прогнозирование тенденций развития национального хозяйства; 3) вьмвление имеющихся резервов эффективности общественного производства; 4) своевременное обеспечение надежной информацией законодательной власти, управленческих, исполнительных и хозяйственных органов, а также широкой общественности.

4этапа: составление программы и плана исследования, сбор материала, статистическая обработка собранного материала, анализ полученных данных и формулировка выборов.
1 этап. При составлении программы необходимо определить объект исследования, который наз-ся стат. совокупность- это группа относительно однородных элементов-единиц наблюдения, объединенных вместе в границах времени и пространства. Каждая ед-ца наблюдения имеет учетные признаки, они м.б.качественными и количественными. Исслед-е м.б.текущим и единовременным. По способу получения информации-непосредственное и анамнестическое наблюдение. По охвату-сполшным и выборочным. Материал сводят в таблицу, она д.иметь краткое и четкое название, кот-е пишут над таблицей. Бывает стат-е подлежащее(основной признак изучаемого явления-горизонтальные строки), стат-е сказуемое(что говорится о подлежащем-вертик-е графы). Простые и сложные таблицы. Простые-1 подлеж-е и 1 сказ-е. Сложные-групповые и комбинационные. Далее изучаем приз-ки стат-й совок-ти:1-распределение,2-средний ур-нь признака,3-вариабельность,4-репрезентативность(представительность),5-корреляция. 2 этап. Сбор материала. Нужно собрать материал по составленной программе на основе опред-х метобов:1-непосредственное наблюдение,2-опрос,3-выкопировки. На каждую ед-цу наблюд-я заполн-ся анкета.
3 этап. Разработка материала. Машинная или ручная обработка. Машинная проводится машинистом на комп-ре. Ручная:проверка собранного материала; разметка приз-в по группам, классификация, шифровка;раскладка карт по группам для подсчетов;графическое изображение показателей. Данные подсчитываются и вносятся в таблицы. Абсолютные и относительные величины. Абсол-е для общей хар-ки явления или признака(число врачей). Относ-е для сравнения признаков:экстенсивный показатель, интенсивный, пок-ль соотношения, наглядности, коэф-т наглядности.
Составление динамических рядов. 4 этап. Включает:осмысливание результатов, написание и оформление работы, выводы, проверка соответствия полученных выводов гипотезе исследования, предложение для внедрения в практику.

4 Сущность. Задачи и организационные формы статистического наблюдения.

Статистическая информация – это совокупность статистических данных, отображающих социально-экономические процессы и используемых в управлении экономикой и общественной жизнью.Сбор статистической информации, то есть статистическое наблюдение, является начальной стадией статистического исследования. Ошибки, допущенные на этом этапе, влияют на правильность и достоверность теоретических и практических выводов. Статистическое наблюдение – это планируемый, систематизированный и научно организованный сбор массовых данных о различных общественно-экономических явлениях и процессах.Основная задача статистического наблюдения (далее наблюдения) – получение достоверных статистических данных.В статистической практике используют две организационные формы наблюдения – отчетность и специально организованные наблюдения.Отчетностьявляется основным источником статистической информации и предусматривает систему регламентированных показателей, характеризующих деятельность предприятий. Она имеет свои преимущества, так как формируется на основе первичного учета, обеспечивающего сопоставление и контроль данных.Различают несколько видов отчетности. Прежде всего, выделяют типовую и специализированную отчетность. Типовая имеет единую форму и содержание для всех предприятий и отраслей народного хозяйства. Специализированная присуща тем предприятиям или производствам, которые имеют специфические особенности.По периодичности представления различают еженедельную, двухнедельную, месячную, квартальную, годовую.По способу представления – срочная (телеграфная) и почтовая.По порядку прохождения отчетность разделяют на централизованную и децентрализованную. Централизованная проходит через систему государственной статистики. Децентрализованная обрабатывается в соответствующих министерствах и ведомствах и сводки представляют статистическим органам.К специально организованным наблюдениям относят: переписи, единовременное наблюдение, опросы, выборочные, монографические и другие обследования.Переписи дают полную характеристику массового явления положением на какую-то дату или определенный момент времени. Например, перепись населения, которая проводится интервалом в 10 лет.Единовременное наблюдение проводят на местах, согласно инструкциям статистического органа. Например, перепись производственного оборудования, остатков сырья и материалов.Специальные обследования, как правило, выборочные. Например, обследования бюджетов семей, уровня цен на рынках. Их роль в перспективе будет возрастать.

5 Програ

5 Програмно- методологические вопросы плана статистического наблюдения

Разработка плана проведения статистического наблюдения является важнейшим этапом подготовки статистического наблюдения. План должен содержать формулировку и решение организационных вопросов, таких как установление целей и задач наблюдения, разработка программ наблюдения, определение объекта и единицы наблюдения, выбор вида и способа наблюдения. Целью наблюдения является получение основного результата статистического исследования.Совокупности единиц, о которых должны быть собраны статистические данные, называютобъектами статистического наблюдения. Прежде чем производить статистическое обследование деятельности организации, необходимо определить отличительные черты и важнейшие признаки изучаемого объекта.Первичный элемент объекта статистического наблюдения, являющийся носителем определенных признаков, называют единицей наблюдения, а первичную ячейку, от которой будут в дальнейшем получены статистические сведения, называют единицей совокупности.Требования, предъявляемые к программе статистического наблюдения:1.программа наблюдения должна содержать все основные для нее признаки, черты, характеризующие те явления и процессы, которые будут в дальнейшем использованы в разработке материалов статистического наблюдения;2 .все контрольные вопросы, входящие в программу наблюдения, должны быть кратко, но четко сформулированы; 3.степень полноты и достоверность полученных в ходе статистического наблюдения данных зависят от качества программы; 4.вопросы, рассматриваемые в данной программе, должны быть изложены в логической последовательности.Статистические формуляры – это специализированные документы определенной формы, которые предназначены для учета и отчетности. В формуляре статистического наблюдения содержатся перечень вопросов программы и места для записи ответов на них. Данный формуляр состоит из: титульной части, которая включает в себя наименование статистического наблюдения и органа, его проводящего, дату и наименование органа, утвердившего данный формуляр; адресная часть формуляра должна содержать запись точного адреса единицы или совокупности единиц наблюдения, их соподчиненность.

6 Ошибки статистического наблюдения, контроль полученных данных.

Точность и достоверность данных является наиболее важным требованием статистики. Точностью считается мера соответствия данных наблюдения действительной их величине,достоверностью – мера объективного отображения ими сущности явлений и процессов.

Ошибки наблюдения – расхождения между данными наблюдения и действительными значениями показателей.

Различают ошибки регистрации и репрезентативности.

Ошибками регистрации называются такие, которые возникают в результате неправильного установления фактов или их неправильной записи. Они бывают случайными или систематическими.

Случайные ошибки возникают вследствие действия случайных причин и искажают данные в ту или иную сторону. Влияние их на обобщающие показатели уравновешивается.

Систематические ошибки приводят к значительным отклонениям общих результатов наблюдений. Они бывают преднамеренные и непреднамеренные (например, непреднамеренной является ошибка, связанная с тенденцией округлять свой возраст людьми старшего поколения, преднамеренные ошибки часто встречаются при составлении отчетности предприятий).

Ошибки репрезентативностивозникают только при несплошном наблюдении в тех случаях, когда отобранная часть совокупности не полностью отражает состав совокупности в целом.

Ошибки наблюдения выявляются путем проверки и контроля достоверности данных. Прежде всего, осуществляют внешний контроль формуляров наблюдений. Проверяют правильность и полноту их заполнения. Затем осуществляют логический и арифметический контроль.

Логический контроль обычно состоит в сопоставлении ответов на взаимосвязанные вопросы, что позволяет выявить несовместимость ответов. Арифметический контроль заключается в проверке всех обобщающих показателей и в согласовании тех показателей, которые выводятся один из другого.

7 Содержание сводки и группировки и их роль в статистическом исследовании.

Применение вероятностных методов в научных исследованиях предполагает использование больших совокупностей. Для установления закономерностей, заложенных в этих данных, необходима их систематизация, которая осуществляется путем построения ряда распределения.Первым шагом к построению ряда распределения является сводка и группировка данных.Статистическая сводка – это упорядочение, систематизация и научная обработка данных.Ее задачи – подсчитать, обобщить материалы наблюдений.Сводки бывают простыми и сложными. Простая сводка – это простой расчет итогов первичного статистического материала. Сложная сводка предусматривает выбор группировочных признаков, установление границ группировок, расчет итогов, а также изложение результатов сводки в виде таблиц и графиков.Группировка состоит в разделении совокупности на группы по существенным для них признакам.При группировке необходимо придерживаться единых научных требований: 1. Проведение всестороннего анализа сущности и природы явления, позволяющего определить его типичные черты и отличия. 2. Четкое определение существенных признаков, по которым она проводится. 3. Обоснованное определение границ интервалов группировок таким образом, чтобы в образованные группы объединялись подобные единицы совокупности, а отдельные группы существенно отличались друг от друга.Особое значение группировок объясняется тем, что они выполняют две функции:1) разделяют совокупности на однородные группы; 2) определяют границы и возможности использования других статистических методов (средних величин, корреляционно-регрессионного и других).

Группировки разделяют на структурные, типологические и аналитические.

Структурные группировки характеризуют распределение качественно однородной совокупности на группы по определенному признаку, так как в границах такой совокупности значения признаков, присущих элементам, варьируются. С помощью таких группировок изучают, например, состав населения по возрастным группам, состав предприятий по числу работающих.С помощью типологических группировок выделяют характерные группы, типы явлений, которые составляют неоднородную совокупность, определяют существенные отличия между ними, а также признаки, являющиеся общими для всех групп. Примером такой группировки является распределение населения Украины по сферам производственной деятельности.Типологические группировки отличаются от структурных только целями исследования, формы их полностью совпадают.При изучении взаимосвязей рассматривается как минимум два признака: факторный (причина) и результативный (следствие).

Аналитические группировки проводятся по факторному признаку, и в каждой группе определяется средняя величина результативного признака. При наличии связи между признаками средние групповые систематически возрастают (прямая связь) или уменьшаются (обратная связь).

8 Определение размера интервала статистической группировки.

Интервал – количественное значение, определяющее и отделяющее одну группу от другой, т.е. он очерчивает количественные границы групп.
Интервалы могут быть равные и неравные. Например: по численности работающих предприятия могут быть разбиты на группы: до 100, 100-200, 200-500, 500-1000, 1000 и более. Это объясняется тем, что изменение признака на 50-100 чел. имеет существенное значение для мелких предприятий, а для крупных – не имеет.
Для группировок с равными интервалами величина (длина, шаг) интервала определяется по формуле:

,
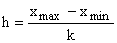где 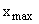, 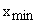– наибольшее и наименьшее значение признака;
к – число групп (интервалов), определяемое по формуле Стерджесса:

,

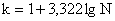где N – число единиц совокупности.

9 Виды и правила построения статистических таблиц.

Статистическими таблицами считают только такие, которые содержат результаты анализа социально-экономических явлений и процессов. В статистических таблицах различают подлежащее и сказуемое. Подлежащим таблицы является такая совокупность, те объекты или их части, которые характеризуются рядом количественных показателей. Показатели, которые характеризуют совокупность, являются ее сказуемым.

В зависимости от построения подлежащего таблицы разделяют на три группы – простые, групповые, комбинационные.

В простых таблицахподлежащее содержит перечень объектов, периодов, дат либо других признаков, которые изучаются. Например, при изучении количества студентов в отдельных странах, подлежащим таблицы является перечень стран, а сказуемым – количество студентов.

Групповые таблицыотличаются тем, что в подлежащем размещаются группы элементов совокупности по одному признаку. Самым простым видом групповых таблиц являются ряды распределения.

В подлежащем комбинационных таблицгруппы по одному признаку разделяются на подгруппы по другим признакам. Иногда в комбинационных таблицах группы по одному признаку размещают в подлежащем, а по другому – в сказуемом.

При составлении таблиц необходимо придерживаться следующих правил:

1. Таблица по возможности должна быть небольшой по размерам.

2. Все заголовки должны формулироваться четко, коротко, содержательно.

3. Если число показателей сказуемого велико, их необходимо пронумеровать. При этом столбцы, в которых приведен перечень объектов или групп, обозначают заглавными буквами алфавита, а столбцы с показателями сказуемого – арабскими цифрами.

4. Если нет сведений о величине явления, то в соответствующей клетке записывают "Нет сведений" или проставляют многоточие; отсутствие явления обозначают тире (-).

5. Количественные показатели в пределах одного столбца должны приводиться с одинаковой точностью (например, до десятых, сотых).

6. Таблицы должны быть закрытыми, то есть с итоговыми результатами; исключением являются аналитические таблицы, в которых расчет
итогов не обязателен.

10 Сущность, задачи и виды средних величин.

Средней величиной называется статистический показатель, который дает обобщенную характеристику количественного признака однородных единиц совокупности.

Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.

Виды средних величин

Средние величины делятся на два больших класса: степенные средние и структурные средние

Степенные средние:

§ Арифметическая

§ Гармоническая

§ Геометрическая

§ Квадратическая

Структурные средние:

§ Мода

§ Медиана

11 Свойства средней арифметической. Способ «моментов».

Простая средняя арифметическая для ряда данных рассчитывается по формуле: Но можно также рассчитать среднюю арифметическую взвешенную как:
Свойства средней арифметической:
(1)Сумма отклонений различных значений признака от среднеарифметической равна нулю: (2) Если от каждого варианта вычесть или к каждому варианту прибавить какое-либо произвольное постоянное число, то средняя увеличится или уменьшится на то же самое число.
(3) Если каждый вариант умножить (разделить) на какое-либо произвольное постоянное число, то средняя увеличится (уменьшится) во столько же раз.
(4)Если веса, или частоты, разделить или умножить на какое-либо произвольное постоянное число, то величина средней не изменится. Это свойство дает возможность заменять веса их удельными весами:
Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом. В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.
Способ моментов предполагает следующие действия: 1)Если возможно, то уменьшаются веса. 2) Выбирается начало отсчета – условный нуль. Обычно выбирается с таким расчетом, чтобы выбранное значение признака было как можно ближе к середине распределения. Если распределение по своей форме близко к нормальному, но за начало отсчета выбирают признак, обладающий наибольшим весом. 3)Находятся отклонения вариантов от условного нуля. 4)Если эти отклонения содержат общий множитель, то рассчитанные отклонения делятся на этот множитель. 5)Находится среднее значение признака по следующей формуле

12 Структурные средние (мода и медиана).

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

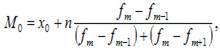
где:

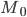§ — значение моды

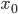§ — нижняя граница модального интервала

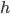§ — величина интервала

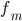§ — частота модального интервала

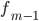§ — частота интервала, предшествующего модальному

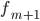§ — частота интервала, следующего за модальным

Медиана —это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот 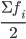, а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

М_е= (n_{(число признаков в совокупности)}+ 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

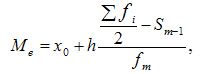
где:

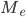§ — искомая медиана

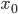§ — нижняя граница интервала, который содержит медиану

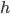§ — величина интервала

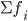§ — сумма частот или число членов ряда

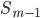§ - сумма накопленных частот интервалов, предшествующих медианному

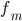§ — частота медианного интервала

13 Необходимость измерения вариации признаков. Размах вариаций.

Вариационными называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности непостоянны, более или менее различаются между собой.

Вариация - колеблемость, изменяемость величины признака у единиц совокупности. Отдельные числовые значения признака, встречающиеся в изу­чаемой совокупности, называют вариантами значений. Недостаточность средней величины для полной характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака.

Абсолютные и средние величины не могут дать всесторонней характеристики изучаемой совокупности, не позволяют судить о структуре совокупности, о внутреннем ее строении. Более полное представление об изучаемой совокупности может быть получено путем исследования различий между единицами совокупности с помощью измерения колеблемости изучаемого признака.

Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности (R = Х_max- X_min). Этот показатель дает самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Зависимость от крайних значений признака придает размаху вариации неустойчивый, случайный характер.

Размах вариации не связан с частотами в вариационном ряду. т. е. с характером распределения. Размах вариации не дает никакой информации об особенностях исследуемых совокупностей и не позволяет оценить степень типичности полученных средних. Область применения этого показа-геля ограничена достаточно однородными совокупностями.

14 Среднее линейное отклонение.

Для характеристики вариации признака нужно знать не только амплитуду (размах) его значений, но и уметь обобщить отклонения всех этих значений от какой-либо типичной для изучаемой совокупности величины. В качестве такой величины используют среднюю арифметическую. Такие показатели вариации, пак среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. основаны на рассмотрении отклонений значений признака Отдельных единиц совокупности от средней арифметической.

Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:

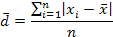
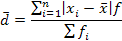
где d - среднее линейное отклонение;

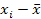| | - абсолютное значение (модуль) отклонения варианта от средней арифметической;

f-частота.

Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая - в рядах с неравными частотами. Необходимость использования в формулах среднего линейного отклонения модулей отклонений вариантов от средней вызвана тем, что алгебраическая сумма этих отклонений равна нулю по свойствам средней арифметической. Среднее линей­ное отклонение показывает, насколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.

16 Методы исчисления дисперсии.

Дисперсия обладает рядом свойств, которые позволяют упростить ее расчеты.

1). Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится:

2) Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А² раз, а среднее квадратическое отклонение — в А раз.

3). Если исчислить средний квадрат отклонений от любой величины А, которая в той или иной степени отличается от средней арифметической х, то он всегда будет больше среднего квадрата отклонений s², исчисленный от средней арифметической:

А именно средний квадрат отклонений при этом будет больше на квадрат разности средней и этой условно взятой величиной, т.е. на

15 Дисперсия альтернативного признака

Дисперсия ( 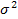) - средняя из квадратов отклоне­ний вариантов значений признака от их средней величины:

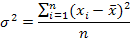
Или 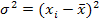для не сгруппированных данных,

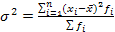для сгруппированных данных.

Дисперсия альтернативного признака, т. е. признака, имеющего два противоположных значения. В таких случаях наличие признака обозначается единицей, а его отсутствие - нулем. Доля единиц, обладающих признаком, обозначается через р, доля остальных единиц - q= 1 - р. Средняя величина альтернативного признака:

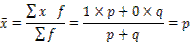
Дисперсия альтернативного признака:

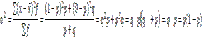
17 Среднее квадратическое отклонение. Коэффициент вариации.

Дисперсия (о*) - средняя из квадратов отклонений вариантов значений признака от их средней величины:

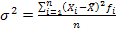
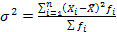
вторая формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).

Среднее квадратическое отклонение (о) представляет собой корень квадратный из дисперсии:

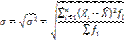
Среднее квадратическое отклонение показывает, насколько е среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.

В статистической практике часто возникает необ­ходимость сравнения вариации различных признаков. При сравнении изменчивости различных при­знаков в совокупности, для оценки интенсивности вариации, для сравнения ее в разных совокупностях ¹ и для разных признаков удобно применять относи - тельные показатели вариации. Эти показатели вычисляются как отношение абсолютных показателей к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблемости:

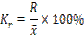
(коэффициент осцилляции);

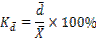
(относительное линейное отклонение).

Коэффициент вариации - наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Со­вокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений, близких к нормальному. Коэффициент вариации применяется для сравнения колеблемости разнородных признаков. Коэффициент вариации часто используется для сравнения размеров вариации в совокупностях, отличающихся друг от друга величиной средней (в совокупностях с разными уровнями):

Оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава. При этом при равенстве коэффициентов вариации для раз­личных признаков или в разных совокупностях вариация в одних случаях может считаться как сильная, а в других - как слабая. Различная сила, интенсивность вариации обусловлены объективны­ми причинами.

18 Ряды распределения, их виды и способы графического изображения.

????

19 Виды и формы связей.