Векторное, смешанное произведение векторов.
ВЕКТОРЫ, ДЕЙСТВИЯ НАД ВЕКТОРАМИ.
Основные определения.
Определение 1.Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.
(Масса тела, объем, время и т.д.)
Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.
(Перемещение, сила, скорость и т.д.)
Обозначения:  ,
,  или
или 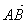 ,
, 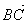 .
.
Геометрический вектор – это направленный отрезок.
Для вектора 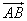 – точка А – начало, точка В – конец вектора.
– точка А – начало, точка В – конец вектора.
Определение 3. Модульвектора – это длина отрезка AB.
Определение 4.Вектор, модуль которого равен нулю, называется нулевым, обозначается 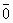 .
.
Определение 5.Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.
Определение 6.Два вектора считаются равными, если они сонаправлены и равны по модулю.
Действия над векторами.
Сложение векторов.
Опр. 6. Суммой двух векторов  и
и  является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
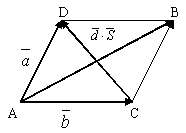
Рис.1.
Опр. 7.Суммойтрех векторов  ,
,  ,
, 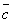 называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Опр. 8.Если А, В, С – произвольные точки, то 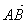 +
+ 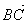 =
= 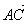 (правило треугольника).
(правило треугольника).
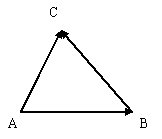
рис.2
Свойства сложения.
1о.  +
+  =
=  +
+  (переместительный закон).
(переместительный закон).
2о.  + (
+ (  +
+ 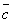 ) = (
) = (  +
+  ) +
) + 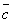 = (
= (  +
+ 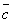 ) +
) +  (сочетательный закон).
(сочетательный закон).
3о.  + (–
+ (–  ) +
) + 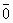 .
.
Вычитание векторов.
Опр. 9.Подразностью векторов  и
и  понимают вектор
понимают вектор 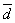 =
=  –
–  такой, что
такой, что  +
+ 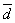 =
=  .
.
В параллелограмме – это другая диагональ СД (см.рис.1).
Умножение вектора на число.
Опр. 10. Произведением вектора  на скаляр k называется вектор
на скаляр k называется вектор
 = k
= k  =
=  k,
k,
имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора  , если k > 0;
, если k > 0;
2. противоположно направлению вектора  , если k < 0;
, если k < 0;
3. произвольно, если k = 0.
Свойства умножения вектора на число.
1о. (k + l)  = k
= k  + l
+ l  .
.
k(  +
+  ) = k
) = k  + k
+ k  .
.
2o. k(l  ) = (kl)
) = (kl)  .
.
3o. 1×  =
=  , (–1) ×
, (–1) ×  = –
= –  , 0 ×
, 0 ×  =
= 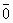 .
.
Свойства векторов.
Опр. 11.Два вектора  и
и  называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
Нулевой вектор 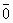 коллинеарен любому вектору.
коллинеарен любому вектору.
Теорема 1. Два ненулевых вектора  и
и  коллинеарны, Û когда они пропорциональны т.е.
коллинеарны, Û когда они пропорциональны т.е.
 = k
= k  , k – скаляр.
, k – скаляр.
Опр. 12. Три вектора  ,
,  ,
, 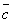 называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
Теорема 2. Три ненулевых вектора  ,
,  ,
, 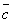 компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
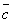 = k
= k  + l
+ l  , k ,l– скаляры.
, k ,l– скаляры.
Проекция вектора на ось.
Теорема 3.Проекция вектора  на ось (направленная прямая) l равна произведению длины вектора
на ось (направленная прямая) l равна произведению длины вектора  на косинус угла между направлением вектора и направлением оси, т.е.
на косинус угла между направлением вектора и направлением оси, т.е. 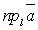 = a × cos a, a = Ð(
= a × cos a, a = Ð(  , l).
, l).
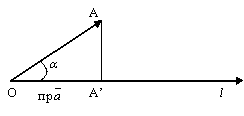
рис.3.
КООРДИНАТЫ ВЕКТОРА
Опр. 13. Проекции вектора  на координатные оси Ох, Оу, Оz называются координатами вектора. Обозначение:
на координатные оси Ох, Оу, Оz называются координатами вектора. Обозначение:  {ax,ay, az}.
{ax,ay, az}.
Длина вектора: 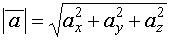

Пример:Вычислить длину вектора 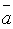
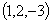 .
.
Решение: 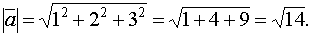
Расстояние между точками 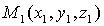 и
и 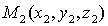 вычисляется по формуле:
вычисляется по формуле: 
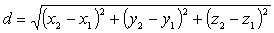 .
.
Пример:Найти расстояние между точками М (2,3,-1) и К (4,5,2).