Второй замечательный предел.
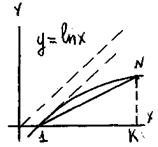 Построим на графике функции y = ln xсекущую MN, где M(1,0), N(1+h,ln(1+h)).Тогда tg
Построим на графике функции y = ln xсекущую MN, где M(1,0), N(1+h,ln(1+h)).Тогда tg 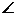 (NMK) = ln(1+h) / h.При N®Mсекущая переходит в касательную и tg
(NMK) = ln(1+h) / h.При N®Mсекущая переходит в касательную и tg 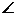 NMK ® tg 450 = =1,т.е. lim (ln(1+h)/h) = 1.Используем тождество elny = y.Тогда
NMK ® tg 450 = =1,т.е. lim (ln(1+h)/h) = 1.Используем тождество elny = y.Тогда
lim (1+h)1/h = lim eln (1+h)/h = elim (ln(1+h)/h) = eпри h ® 0
При замене h = 1/x,где x ® ¥,получаем другую запись предела
(a) lim ln(1+x) / x = 1; (b) lim (1+x)1/x = e ; (c) lim (1+1/x)x = e
x ® 0 x ® 0 x ® ¥
Общие правила раскрытия неопределенностей
1. {0/0}При вычислении пределов дробно-рациональных функций
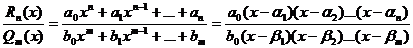
используется основная теорема алгебры, т.е. многочлены представляется как произведение двучленов ( Пр. x2 + bx + c = (x – x1)(x – x2) ) и взаимно сокращаются одинаковые.
Пр. 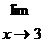
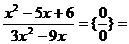
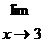
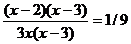
2. {¥ / ¥}Вынесем х в максимальной степени за скобки в Rn(x) , Qm(x) и сократим
Пр. 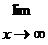
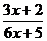 = {¥/¥} =
= {¥/¥} = 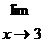
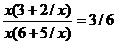
3. {¥ - ¥}Проведем вычитание дробей или умножим числитель и знаменатель разности на сопряженный двучлен
Пр. 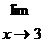
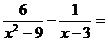 {¥ - ¥} =
{¥ - ¥} = 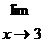
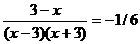
4. 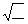 Для того чтобы избавится от двучленов с корнями можно умножить их на сопряженные двучлены
Для того чтобы избавится от двучленов с корнями можно умножить их на сопряженные двучлены
Пр. 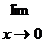
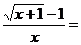 {0/0} =
{0/0} = 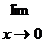
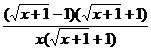 =
= 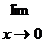
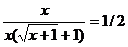
5. {0 ¥}В общем случае : 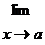
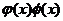 = {0 ¥} =
= {0 ¥} = 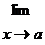
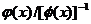 = {0/0}
= {0/0}
6. { 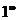 }, {
}, { 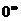 }, {
}, { 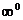 }В случае показательно-степенной функции
}В случае показательно-степенной функции 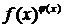 тип
тип
неопределенности меняем с помощью тождества eln y= y ,т.е.
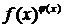 = exp( ln
= exp( ln 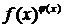 ) = exp(
) = exp( 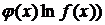
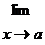
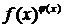 = exp(
= exp( 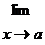
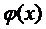 ln
ln 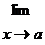
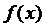 ) = eB lnA = AB
) = eB lnA = AB
где A = 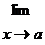
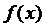 > 0 ; B =
> 0 ; B = 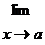
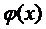
т.е. при переходе к пределу показательно-степенной функции основание и степень заменяются на их пределы.
Пр. 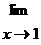
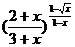 =AB =(3/4)1/2 ,т.к.A =
=AB =(3/4)1/2 ,т.к.A = 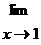
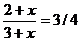 ;B =
;B = 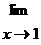
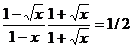
В случае А = 1, В = ¥используют преобразование
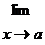
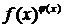 =
= 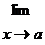
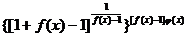 = exp {
= exp { 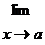 [f(x) – 1]
[f(x) – 1] 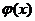 },
},
т.е. А = e , B = 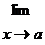 [f(x) – 1]
[f(x) – 1] 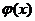
Пр. 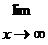
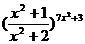 = exp {
= exp { 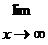
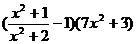 } = e-7 ,т.к.
} = e-7 ,т.к.
А = 1, В = ¥
Непрерывность функции.
 С понятием предела функции связано другое важное понятие – непрерывность функции.На графике непрерывным функциям соответствуют непрерывные линии.
С понятием предела функции связано другое важное понятие – непрерывность функции.На графике непрерывным функциям соответствуют непрерывные линии.
Пусть y = f(x) определена в точке хo и ее окрестности. Величина  х = х – хoназ. приращением аргумента,
х = х – хoназ. приращением аргумента,  y = y – yo- соответствующим приращением функции.
y = y – yo- соответствующим приращением функции.
Опр.1Функция y = f(x)наз. непрерывнойв точке х, если она определена в этой точке и ее окрестности и бесконечно малому приращению аргумента  хсоответствует бесконечно малое приращение функции
хсоответствует бесконечно малое приращение функции  y, т.е.
y, т.е.
lim  y = 0при
y = 0при  х
х  0( 1 )
0( 1 )
Следствие:Основные элементарные функции являются непрерывными во всех точках области определения D(f), т.к. они имеют предел в каждой из точек и удовлетворяют условию ( 1 )
y = ax ,  y =
y = 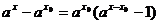 , lim
, lim  y =
y = 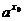 lim (a
lim (a 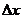 - 1) = 0при
- 1) = 0при  х
х  0
0
y = loga x ,  y = loga(x +
y = loga(x +  x) - loga x = loga (1 +
x) - loga x = loga (1 +  x/x), lim
x/x), lim  y = lim loga(1 +
y = lim loga(1 +  x/x) = 0
x/x) = 0
y = x2 ,  y = (x +
y = (x +  x)2 - x2 = 2x
x)2 - x2 = 2x  x + (
x + (  x)2 , lim
x)2 , lim  y = lim [2x
y = lim [2x  x + (
x + (  x)2 ] = 0
x)2 ] = 0
Опр.2Функция y = f(x)наз. непрерывной в точке хo ,если ее предел в хoсовпадает со значением функции в этой точке.
lim f(x) = f(xo)при x  xo( 2 )
xo( 2 )
Покажем эквивалентность этих определений:
lim  y = 0
y = 0 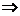 lim(f(x) – f(xo)) = 0
lim(f(x) – f(xo)) = 0 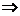 lim f(x) = f(xo), при
lim f(x) = f(xo), при
 x
x  0 x
0 x  xo const x
xo const x  xo
xo
Условие ( 2 ) позволяет для непрерывных функций переход к пределу функции заменить на переход к пределу аргумента
lim f(x) = f (lim x ) , при( 3 )x  xo x
xo x  xo
xo
Для y = f(x) определенной на [a,b]предельный процесс около внутренней точки x(a < x < b)можно организовать двумяспособами, подходя к точке xслева или справа lim f(x) = f(xo – 0) , lim f(x) = f(xo + 0)
x  xo - 0 x
xo - 0 x  xo + 0
xo + 0
Это левосторонний и правосторонний пределы.
Опр.3Функция y = f(x)наз. непрерывной в точке хo ,если ее левосторонний и правосторонний пределы совпадаютf(xo – 0) = f(xo+ 0) = f(xo)
Опр.Функция y = f(x)наз. непрерывной на промежутке [a,b] , если она непрерывна в каждой его точке. На концах lim f(x) = f(a) , lim f(x) = f(b)
x  a + 0 x
a + 0 x  b - 0
b - 0
Точки разрыва.
Непрерывность функции может быть нарушена в отдельных точках. Три типа точек разрыва :
1) x0 - устранимая точка разрыва, когда f(x0 - 0) = f(x0 + 0),но в самой точке х0функция не определена;
2) x0 - точка разрыва 1 рода, когда f(x - 0) 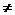 f(x + 0), но пределы конечны;
f(x + 0), но пределы конечны;
3) x0 - точка разрыва 2 рода, когда f(x - 0) 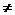 f(x + 0) и пределы бесконечны;
f(x + 0) и пределы бесконечны;
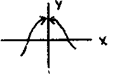

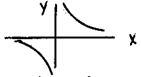
Пр.
y = sinx/ x, x = 0 f(x) = |x| /x, x = 0 y = 1/x, x = 0
Свойства функций, непрерывных в точке .
1)Если функции g(x) и h(x) непрерывны в точке хo, то функции g(x) + h(x),
g(x) h(x), g(x)/h(x)при h(xo) 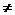 0также являются непрерывными функциями.
0также являются непрерывными функциями.
lim ( g(x) + h(x) ) = lim g(x) + lim h(x) = g(xo) + h(xo)
x  xo x
xo x  xo x
xo x  xo
xo
Для остальных функций доказательство аналогично.
2)Сложная функция, составленная из непрерывных функций, также является непрерывной.
Док-во. Пусть функция y = g(z)непрерывна в точке zo ,а z = h(x)в точке хo ,причем, zo = h(xo).По определению непрерывности lim h(x) = zo , lim g(z) = g(zo)
x – xo z – zo
Т.к. предел сложной функциипри х  хoравен значению функции в точке хo
хoравен значению функции в точке хo
lim g( h(x) ) = lim g(z) = g(zo) = g (h(xo) )
то функция является непрерывной .
Следствие.Элементарные функции образуются из основных элементарных функций с помощью арифметических операций или являются их суперпозициями. Поскольку основные элементарные функции непрерывны, то в силу свойств 1) и 2) все составленные из них элементарные функции также непрерывны и изображаются на графиках сплошными линиями в области своего определения.
