Свойства скалярного произведения двух векторов

1. Скалярное произведение двух векторов обладает свойством переместительности: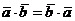

Доказательство. По определению .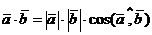

Очевидно, что 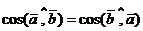. Если же, кроме того, воспользуемся свойством переместительности произведения чисел, то получим .

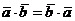2. Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию другого вектора на направление первого, то есть 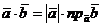или .

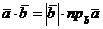Доказательство. По определению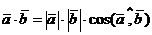

С другой стороны, по теореме о проекции вектора на ось, 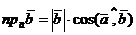. Из двух последних равенств с очевидностью вытекает, что .

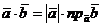Аналогично можно доказать, что .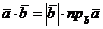

3. Проекция вектора на ось равна скалярному произведению этого вектора на орт рассматриваемой оси, то есть 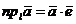, где 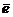- орт оси .

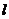Доказательство. Сформулированное свойство по существу является частным случаем рассмотренного выше свойства 2 и с очевидностью из него вытекает, если принять вектор 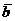равным орту .

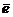4. Скалярный множитель можно вынести за знак скалярного произведения двух векторов: .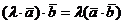

Доказательство. В силу свойства 2 скалярного произведения двух векторов 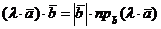, или, с учетом теоремы о проекции на ось произведения вектора на скаляр, .

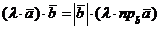Если же, кроме того, принять во внимание свойства сочетательности и переместительности произведения чисел, а также свойство 2 скалярного произведения двух векторов, то получим 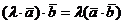, что и требовалось доказать.

5. Скалярное произведение двух векторов обладает свойством распределительности: .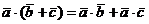

Доказательство. Согласно свойству 2 скалярного произведения двух векторов, .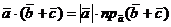

Воспользуемся во втором множителе правой части этого равен­ства теоремой о проекции суммы векторов на ось. Получим: 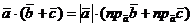, или, в силу свойства распределительности действий над числами, .

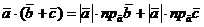Если же снова применить свойство 2 скалярного произведения двух векторов, то придем к выводу, что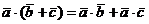

6. Имеет место равенство:

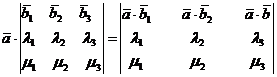
Доказательство. Воспользуемся равенством:

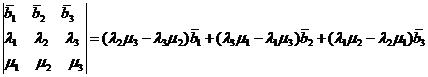
Тогда, в силу свойств 4 и 5 скалярного произведения двух векторов, имеем

,

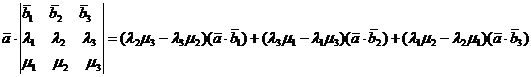то есть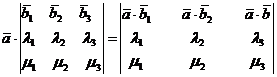

7. Скалярное произведение вектора самого на себя равно квадрату длины этого вектора: .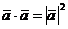

Доказательство. По определению скалярного произведения двух векторов 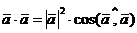, откуда с очевидностью следует, что .

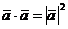Следствие. Длина вектора равна арифметическому значению корня квадратного из скалярного произведения вектора самого на себя: .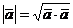

Доказательство. Справедливость этого утверждения с очевидностью следует из свойства 7.

8. Имеет место следующая таблица скалярных произведений координат ортов:

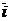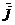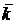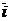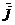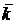Справедливость этой таблицы непосредственно следует из определения скалярного произведения двух векторов.

9. Скалярное произведение двух векторов равно сумме произведений одноимённых проекций этих векторов на координатные оси, т.е.:

.

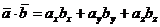Доказательство. Разложим каждый из векторов 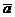и 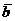по координатным ортам: 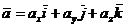и .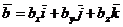

Тогда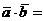

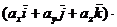
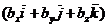
Воспользовавшись свойствами скалярного произведения двух векторов, получим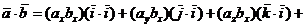

,

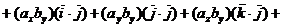
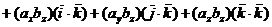или, согласно таблице скалярных произведений координатных ортов, 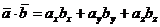, что и требовалось доказать.

Следствия

1). Длина вектора равна арифметическому значению корня квадратного из суммы квадратов проекций этого вектора на координатные оси:

.

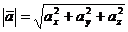Доказательство. Действительно, 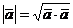и так как 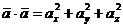, то .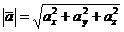

2). Расстояние между точкам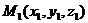и и 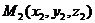равно арифметическому значению корня квадратного из суммы квадратов разностей одноименных декартовых координат этих точек, то есть

.

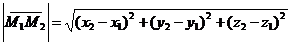Доказательство. Действительно, 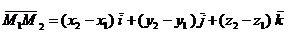и потому .

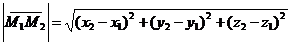3). Сумма квадратов направляющих косинусов любого вектора равна единице, то есть

.

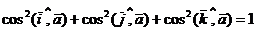Доказательство. Как было показано ранее, для орта вектора 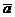справедливо следующее равенство: 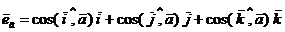. Кроме того, 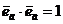. Следовательно, .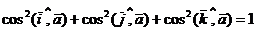