Отображения на множество (сюръективные отображения)

Определение.

Пусть 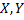– некоторые множества, .

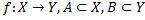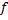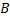Будем говорить, что отображает множество на множество , если

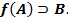
Определение.

Пусть 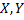– некоторые множества, .

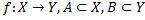Будем говорить, что 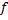– отображение на множество 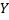(= сюръективное=эпиморфное), если

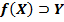
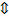
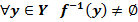
(для любого 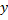его прообраз не пуст.)

Пример.

Указать все подмножества , которые отображаются на множество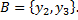

Определение.

Пусть 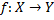, будем говорить, что 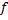– отображение на множество 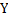(сюръективное отображение=эпиморфное), если

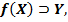
(т.е. образ множества содержит всё )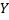

и обозначать

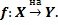
Замечание №1.

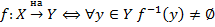
(т.е. у любого 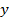его прообраз не пуст.)

Свойство эпиморфности: прообраз любого 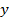не пуст.

Замечание №2.

Так как для любого отображения 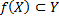, то для отображения на 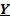(т.е. 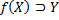), имеем

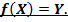
Замечание №3.

Между инъективностью и сюръективностью никакой связи нет.

Изоморфизмы (биективные отображения)

Определение изоморфизма (биективного отображения)

Определение.

Пусть 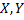– некоторые множества, .

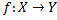Если 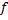является отображением на 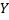(сюръективным отображением) и является взаимно-однозначным (инъективным), то говорят, что отображение 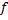является биективным (=биекцией множества на множество 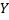= изоморфизмом множеств )

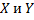Замечание.

Биективность означает, что для любого 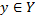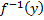является одноэлементным множеством, т.е.

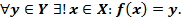
Примеры.

I. Построить биекцию отрезков 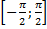и .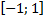

II. Пусть – произвольное множество.

Тождественным отображением множества на себя называют отображение

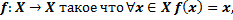
и обозначают

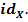
III. Перестановка множества.

Перечислите все перестановки трёхэлементного множества .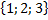

Замечание.

Для конечных множеств 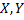биекция множества на множество 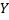существует в том и только в том случае, когда оба множества 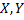имеют одинаковое число элементов.

Для бесконечных множеств можно установить биекцию множества на его собственное подмножество.

Пример №1.

IV. Построить биекцию между множеством натуральных чисел 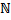и множеством чётных натуральных чисел .

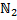V. Построить биекцию между множеством целых чисел 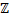и множеством чётных целых чисел .

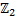VI. Построить биекцию между интервалом 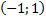и действительной прямой .

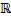Пример №2.

Какие из следующих отображений являются, инъективными, какие сюръективными, какие биективными?

1) ;

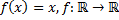2) ;

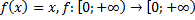3) ;

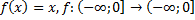4) ;

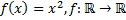5) ;

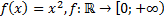6) ;

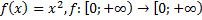7) ;

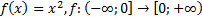8) ;

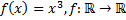9) ;

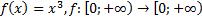10) ;

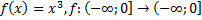11) ;

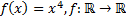12) ;

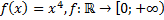13) ;

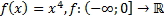14) ;

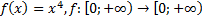15) ;

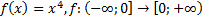16) ;

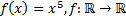17) ;

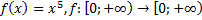18) ;

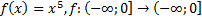19) ;

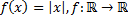20) ;

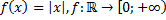21) ;

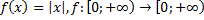22) ;

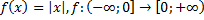23) ;

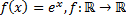24) ;

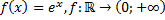25) ;

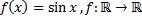26) ;

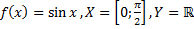27) ;

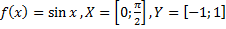28) ;

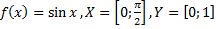29) ;

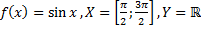30) ;

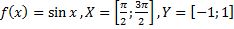31) ;

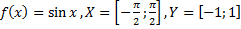32) ;

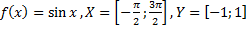33) ;

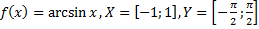34) ;

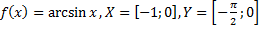35) ;

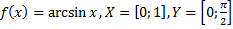36) ;

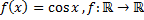37) ;

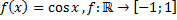38) ;

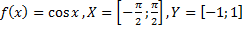39) ;

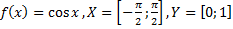40) ;

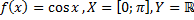41) ;

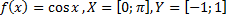42) ;

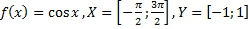43) ;

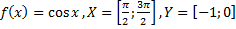44) ;

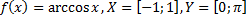45) ;

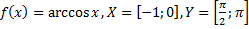46) ;

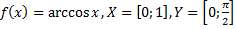47) ;

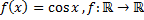48) ;

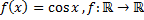49) ;

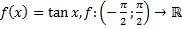50) ;

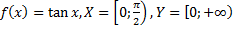51) ;

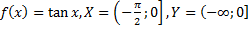52) ;

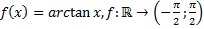53) ;

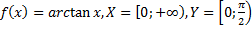54) ;

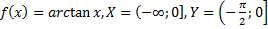55) ;

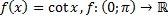56) ;

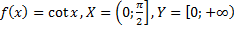57) ;

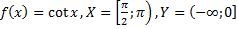58) ;

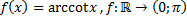59) ;

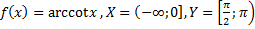60) ;

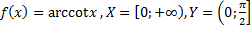Конечные и бесконечные множества.

Определение.

Говорят, что множество является конечным, если существует натуральное число 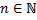, такое что можно осуществить биекцию множества 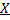на множество 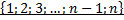, т.е. “пронумеровать” все элементы множества (каждый по одному разу) натуральными числами (от 1 до n):

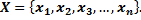
Такое число 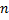существует единственное и называется количеством элементов множества

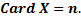
Все остальные множества – бесконечные.

Мощность множества

Определение.

Пусть 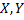– произвольные множества, говорят, что множества 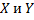имеют одинаковую мощность (являются равномощными), если существует биекция множества на множество .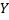

Замечание.

Конечные множества равномощны тогда и только тогда, когда имеют одинаковое число элементов.

Замечание.

Бывают неравномощные бесконечные множества. К примеру, множество 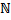неравномощно множеству .

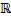Определение.

Множество, равномощное множеству 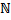, называют счётным.

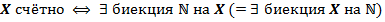
Определение.

Множество – не более чем счётное, если – конечно или счётно.

Теорема.

Множество 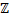счётно.

Доказательство.

Теорема.

Бесконечное подмножество счётного множества счётно.

Доказательство.

Замечание.

Любые 2 счётных множества равномощны.

Доказательство.

Теорема.

Прямое (декартово) произведение счётных множеств счётно.

Теорема.

Множество всех рациональных чисел 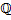счётно.

Композиция отображений

Определение.

Пусть 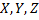– некоторые множества.

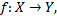
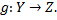
Композицией отображени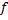й и 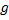называется отображение

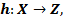
такое что

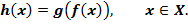
Обозначение композиции

Композиция отображени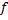й и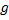

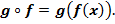
Замечание №1.

Выражение 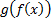имеет смысл, т.к. .

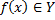Замечание №2.

Переставлять 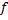и 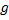местами вообще говоря нельзя.

Пример.

Пусть

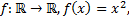
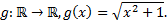
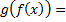
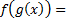
Замечание №3.

Аналогично можно определить композицию не 2-х, а 3-х и более отображений.

Придумайте примеры.

Обратное отображение

Пусть 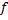– биекция множества на множество .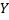

Рассмотрим отображение 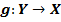, которое каждому 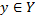сопоставляет 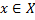, такое что 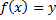, т.е.

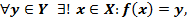
(существование и единственность такого элемента 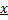следует из определения биекции)

Такое отображение 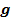называется обратными обозначается символом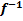

(т.е. )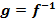

Примеры.

I. Пусть .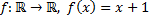

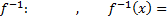
II. Пусть .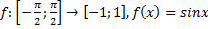

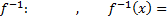
Замечание.

Пусть 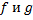– отображения

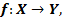
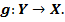
Тогда

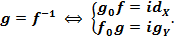
Функции и действия над ними

Сумма функций.

Определение.

Пусть 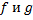– функции

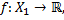
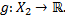
Суммой функций 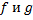называется функция

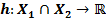
такая что

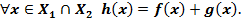
Пример.

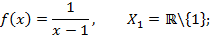
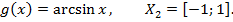
Тогда

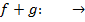
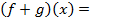
Разность функций.

Определение.

Пусть 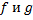– функции

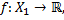
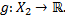
Разностью функций 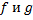называется функция

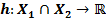
такая что

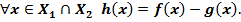
Произведение функций.

Определение.

Пусть 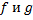– функции

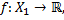
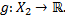
Произведением функций 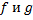называется функция

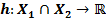
такая что

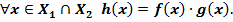
Частное функций.

Определение.

Пусть 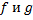– функции

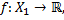
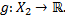
Пусть

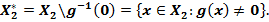
Частным функций 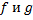называется функция

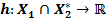
такая что

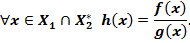
Степень функции.

Замечание.

Используя определения произведения и частного можем определить натуральную и целую степени функции.

Определение.

Пусть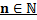

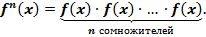
Пусть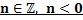

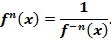
(функция 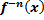определена, т.к. .)

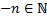Замечание.

Нельзя путать

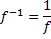
с обратным отображением и обозначением прообраза.