Положительно определенные квадратичные формы
Определение. Квадратичная форма от n неизвестных называется положительно определенной, если ее ранг равен положительному индексу инерции и равен числу неизвестных.
Теорема.Квадратичная форма положительно определена тогда и только тогда, когда на любом ненулевом наборе значений переменных принимает положительные значения.
Доказательство.Пусть квадратичная форма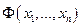 невырожденным линейным преобразованием неизвестных
невырожденным линейным преобразованием неизвестных
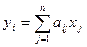 ,
, 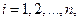
приведена к нормальному виду
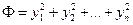 .
.
Для любого ненулевого набора 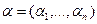 значений переменных
значений переменных 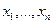 хотя бы одно из чисел
хотя бы одно из чисел 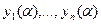 отлично от нуля, т.е.
отлично от нуля, т.е. 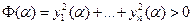 . Необходимость теоремы доказана.
. Необходимость теоремы доказана.
Предположим, что квадратичная форма 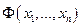 принимает положительные значения на любом ненулевом наборе переменных, но ее положительный индекс инерции
принимает положительные значения на любом ненулевом наборе переменных, но ее положительный индекс инерции 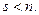 Невырожденным линейным преобразованием неизвестных
Невырожденным линейным преобразованием неизвестных
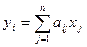 ,
, 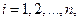
приведем ее к нормальному виду. Без ограничения общности можно считать, что в этом нормальном виде квадрат последней переменной либо отсутствует, либо входит в нее со знаком минус, т.е. 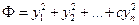 , где
, где 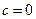 или
или 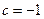 . Предположим, что
. Предположим, что 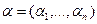 – ненулевой набор значений переменных
– ненулевой набор значений переменных 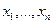 , полученный в результате решения системы линейных уравнений
, полученный в результате решения системы линейных уравнений
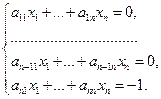
В этой системе число уравнений равно числу переменных и определитель системы отличен от нуля. По теореме Крамера система имеет единственное решение, и оно ненулевое. Для этого набора 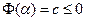 . Противоречие с условием. Приходим к противоречию с предположением, что и доказывает достаточность теоремы.
. Противоречие с условием. Приходим к противоречию с предположением, что и доказывает достаточность теоремы.
С помощью этого критерия нельзя по коэффициентам установить, положительно ли определена квадратичная форма. Ответ на такой вопрос дает другая теорема, для формулировки которой введем еще одно понятие. Главные диагональные миноры матрицы 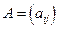 – это миноры, расположенные в ее левом верхнем углу:
– это миноры, расположенные в ее левом верхнем углу:
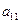 ,
, 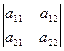 ,
, 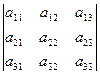 , … ,
, … , 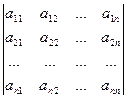 .
.
Теорема.Квадратичная форма положительно определена тогда и только тогда, когда все ее главные диагональные миноры положительны.
Доказательствопроведем методом полной математической индукции по числу n переменных квадратичной формы f.
Гипотеза индукции. Предположим, что для квадратичных форм с числом переменных меньшим n утверждение верно.
Рассмотрим квадратичную форму 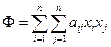 от n переменных. Соберем в одну скобку все слагаемые, содержащие
от n переменных. Соберем в одну скобку все слагаемые, содержащие 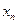 . Оставшиеся слагаемые образуют квадратичную форму
. Оставшиеся слагаемые образуют квадратичную форму 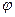 от
от 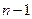 переменных. По гипотезе индукции для нее утверждение верно.
переменных. По гипотезе индукции для нее утверждение верно.
Предположим, что квадратичная форма 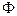 положительно определена. Тогда и квадратичная форма
положительно определена. Тогда и квадратичная форма 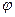 положительно определена. Если предположим, что это не так, то найдется ненулевой набор значений переменных
положительно определена. Если предположим, что это не так, то найдется ненулевой набор значений переменных 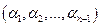 , для которого
, для которого 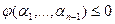 и, соответственно,
и, соответственно, 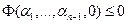 , а это противоречит тому, что квадратичная форма
, а это противоречит тому, что квадратичная форма 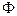 положительно определена. По гипотезе индукции все главные диагональные миноры квадратичной формы
положительно определена. По гипотезе индукции все главные диагональные миноры квадратичной формы 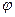 положительны, т.е. все первые
положительны, т.е. все первые 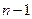 главные миноры квадратичной формы f положительны. Последний главный минор квадратичной формы
главные миноры квадратичной формы f положительны. Последний главный минор квадратичной формы 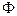 – этоопределитель ее матрицы. Этот определитель положителен, так как его знак совпадает со знаком матрицы ее нормального вида, т.е. со знаком определителя единичной матрицы.
– этоопределитель ее матрицы. Этот определитель положителен, так как его знак совпадает со знаком матрицы ее нормального вида, т.е. со знаком определителя единичной матрицы.
Пусть все главные диагональные миноры квадратичной формы 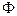 положительны, Тогда положительны все главные диагональные миноры квадратичной формы
положительны, Тогда положительны все главные диагональные миноры квадратичной формы 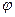 из равенства
из равенства 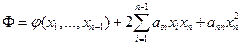 . По гипотезе индукции квадратичная форма
. По гипотезе индукции квадратичная форма 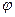 положительно определена, поэтому существует невырожденное линейное преобразование переменных
положительно определена, поэтому существует невырожденное линейное преобразование переменных 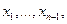 которое приводит форму
которое приводит форму 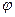 к виду суммы
к виду суммы 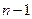 квадратов новых переменных
квадратов новых переменных 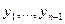 . Это линейное преобразование можно дополнить до невырожденного линейного преобразования всех переменных
. Это линейное преобразование можно дополнить до невырожденного линейного преобразования всех переменных 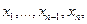 полагая
полагая 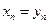 . Квадратичная форма этим преобразованием приводится к виду
. Квадратичная форма этим преобразованием приводится к виду
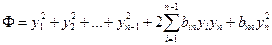 .
.
Дополним до полного квадрата слагаемые с 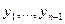
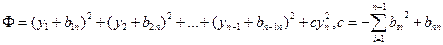 .
.
Невырожденное линейное преобразование
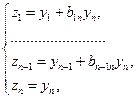
приводит квадратичную форму 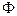 к каноническому виду
к каноническому виду 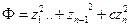 . Определитель матрицы этого канонического вида равен
. Определитель матрицы этого канонического вида равен 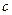 и знак
и знак 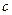 совпадает со знаком определителя матрицы квадратичной формы
совпадает со знаком определителя матрицы квадратичной формы 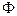 , который положителен по условию. Из того, что
, который положителен по условию. Из того, что 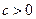 следует, что положительный индекс квадратичной формы
следует, что положительный индекс квадратичной формы 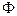 равен n, т.е. форма
равен n, т.е. форма 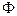 положительно определена.
положительно определена.
