В виде суммы какого наименьшего количества точных квадратов можно представить число 2010?

Нижегородская (VIII открытая) городская математическая олимпиада школьников

г. Нижний Новгород, НФ ГУ-Высшая Школа Экономики, 12 декабря 2010 года

Председатель жюри – профессор НФ ГУ-ВШЭ, декан факультета бизнес-информатики Валерий Александрович Калягин. Вариант подготовлен руководителем Школы информационных технологий и математики при Центре довузовской подготовки НФ ГУ-ВШЭ Дмитрием Юрьевичем Кузнецовым.

УСЛОВИЯ И ИДЕИ РЕШЕНИЙ ЗАДАЧ

Класс

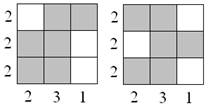1. Винтик и Шпунтик в клетчатом квадрате 3´3 (каждый – в своём) закрасили клетчатый многоугольник. Затем они записали снизу от каждой вертикали и слева от каждой горизонтали числа, показывающие, сколько закрашенных клеток отмечено в соответствующем вертикальном или горизонтальном ряду, стёрли свои многоугольники и отдали Незнайке свои листки с квадратами и написанными на них числами. Незнайка увидел, что ему передали два абсолютно одинаковых листка, и сказал, что у Винтика и Шпунтика были одинаковые многоугольники. Верно ли, что Незнайка обязательно оказался прав?

Ответ:Незнайка не обязательно прав, т.к. у Винтика и Шпунтика могли оказаться одинаковые листочки при разных многоугольниках, например, как показано на рисунке.

2. В ряд выписаны все натуральные числа от 1 до 2010 и в 2009 промежутках между ними расставляются произвольным образом знаки + и -. Какое наименьшее положительное значение может принимать полученное числовое выражение?

Ответ: 1. Доказательство: Т.к. в данной целочисленной знакопеременной сумме будет нечётное (1005) количество нечётных слагаемых, то вся сумма будет нечётной. Значит, минимальное положительное значение, которое она может принимать, равно 1. Приведём пример расстановки + и -, дающий значение 1. Среди первых 6 чисел знаки расставим следующим образом: 1-2-3+4-5+6, что даёт 1. Затем разобьём остальные 2004 числа на четвёрки подряд идущих и в каждой следующей четвёрке (с учётом места перед первым числом четвёрки) расставим знаки по следующему правилу: +, -, -, +, что даст 0, т.к. n-(n+1)-(n+2)+(n+3)=0. Т.о. вся сумма будет равна 1.

Комментарий: фактически это задача С6 с ЕГЭ-2010. И на нашу олимпиаду поставлена для сравнения, как последние номера ЕГЭ решают восьмиклассники. Кроме того, в решении совсем необязательно говорить о нечётности, т.к. меньше 1 натуральных чисел нет:J. Но при решении других задач ссылка на чётность может оказаться очень важной – см.задачу 9.1-11.2.

3. На каком наименьшем квадратном клетчатом поле можно расставить полный комплект кораблей для игры в «морской бой» (1 корабль 1´4, 2 корабля 1´3, 3 корабля 1´2 и 4 корабля 1´1)? Корабли не могут соприкасаться между собой ни сторонами, ни вершинами.

Ответ: 7´7. Пример расстановки для доски 7´7 на рис. Доказательство оценки: 1-й способ: Корабль 1´4 содержит ровно 10 узлов клетчатой решётки, корабль 1´3 - 8 узлов, 1´2 - 6 узлов, 1´1 - 4 узла, тогда для всех кораблей надо не менее 10+2×8+3×6+4×4=60 узлов, значит, узлы должны образовывать решётку размера не менее чем 8´8, т.е. клетчатая доска должна быть размера не менее 7´7.

2-й способ: Предположим, что нам удалось разместить корабли на меньшем поле, значит, мы сможем их разместить и на поле 6´6. Разобьём поле 6´6 на 9 квадратов 2´2. В каждом таком квадрате могут находиться максимум две клетки кораблей, иначе корабли будут касаться друг друга сторонами. Значит, на поле может быть не более 9×2=18 клеток всех кораблей. А всего корабли вместе содержат 4+2×3+3×2+4×1=20>18 клеток. Противоречие. Значит, разместить корабли можно только на поле размера не меньше 7´7. А на этом поле их можно разместить даже без соприкосновения – см. рис.

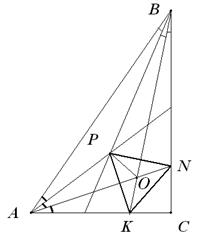4. В прямоугольном треугольнике АВС проведены трисектрисы острых углов, причём AN и BK – дальние от гипотенузы АВ трисектрисы, а две ближние к гипотенузе трисектрисы пересекаются в точке P (трисектрисы делят угол на три равные части, точки N и K лежат на сторонах треугольника). Докажите, что треугольник PNK – равносторонний.

Доказательство:Введём O – точку пересечения трисектрис AN и BK. Пусть ÐA=3a, ÐB=3b, тогда 3a+3b=90° и a+b=30°. Тогда ÐAOB=180°–2a–2b=180°–60°=120°, а точка Р в треугольнике АОВ будет точкой пересечения биссектрис, значит, ÐАОР=ÐВОР=60°. Но и ÐАОК=ÐBON=180°–ÐАОВ=60°. Тогда треугольники APO и AKO равны (по стороне и двум прилежащим углам). Аналогично равны треугольники BPO и BNO. Значит, KO=OP=ON. Кроме того, ÐKOP=ÐPON=ÐNOK=120°, следовательно, треугольники KOP, PON и NOK равны между собой. Значит, KP=PN=NK, т.е. PNK – равносторонний треугольник.

5. В клетки таблицы 2010´2010 по своему усмотрению по одному ставят в некотором порядке все натуральные числа от 1 до 4040100=2010², причём запрещается допускать ситуацию, когда в какой-нибудь строке или в каком-нибудь столбце сумма выставленных на данный момент чисел даёт остаток 1 при делении на 3. Какое наибольшее количество чисел можно поставить по этому правилу?

Ответ:все 2010² чисел.Решение:Разобьём доску на 1005² квадратов 2´2, затем в 673350 из них по очереди делаем следующее: сначала ставим по диагонали 2 числа с остатком 2, затем по другой диагонали - 2 числа с остатком 1, потом переходим к следующему квадрату 2´2. В результате все 1346700=670×2010 чисел с остатком 2 и все 1346700 чисел с остатком 1 будут выставлены, при этом суммы чисел в столбцах и строках на каждом шаге будут иметь остатки 2 и 0. После этого заполняем остальные клетки оставшимися числами, кратными 3, которые никак уже не повлияют на остатки сумм.

Класс

1. В ряд выписаны все натуральные числа от 1 до 11 и в 10 промежутках между ними расставляются произвольным образом знаки + и -. Какое наименьшее положительное значение может принимать полученное числовое выражение?

Ответ: 2. Доказательство: Т.к. в данной целочисленной знакопеременной сумме будет чётное (6) количество нечётных слагаемых, то вся сумма будет чётной. Значит, минимальное положительное значение, которое она может принимать, равно 2. При этом значение 2 можно получить, например, расставив знаки следующим образом: 1-2+3-4-5-6-7-8+9+10+11=34-32=2.

2. Для положительных a и b выполняется равенство 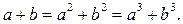Докажите, что a=b=1.

Доказательство 1: 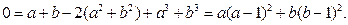Откуда при положительных числах и получаем, что оба числа равны 1.

Доказательство 2: Из формулы суммы кубов 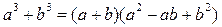и равенства 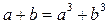при положительных числах следует, что 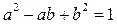. Тогда с учётом равенства 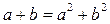получим, что 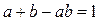. Переносим всё в правую часть и раскладываем на множители 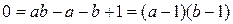, откуда и следует, что одно из чисел a или b равно 1. После подстановки этого значения в исходное равенство найдём, что и второе число также равно 1.

3. Перед двумя игроками открыто (числами вверх) лежит полный комплект из 28 доминошек (0-0, 0-1, 0-2, …, 5-6, 6-6). Игроки по очереди за один ход берут по одной доминошке и на своё усмотрение составляют из чисел этой доминошки квадратное уравнение x²+ax+b=0, где a и b - числа взятой доминошки. По окончании игры подводится итог по следующему правилу: если больше половины из 28 получившихся уравнений не имеют корней, то выиграл первый; если больше половины уравнений имеют корни, то выиграл второй; если таких уравнений поровну, то - ничья. Кто из игроков выигрывает при правильной игре?

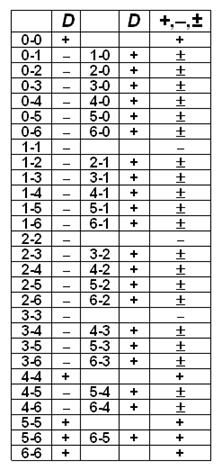Ответ:при правильной игре выигрывает второй.Доказательство:Доминошку будем считать положительной (+), если при любой подстановке её чисел вместо коэффициентов a и b квадратное уравнение x²+ax+b=0 будет иметь корни, т.е. его дискриминант D=a²-4b будет неотрицательным. Доминошку будем считать отрицательной (-), если при любой подстановке уравнение не будет иметь корней, т.е. дискриминант D<0. И доминошку будем считать нейтральной (±), если при одной подстановке уравнение имеет корни, а при другой – не имеет. Составим таблицу, в которой для каждой доминошки определим, какой она является (+, - или ±). Для этого проверим значение дискриминанта D=a²-4b для каждой доминошки. Получаем, что всего 5 положительных (+), 3 отрицательных (-) и 20 нейтральных (±) доминошек. Тогда второй игрок применяет следующую стратегию. За первые 10 пар ходов (первый-второй игрок) он имеет возможность взять 10 нейтральных доминошек и создать с их помощью 10 уравнений, имеющих корни. Кроме того, независимо от других ходов обоих игроков ещё хотя бы 5 уравнений будут с корнями за счёт положительных доминошек. Таким образом, второй игрок может гарантированно получить не менее 15 уравнений с корнями, т.е. больше половины всех уравнений. Значит, применив эту стратегию, второй игрок выигрывает.

4. На стороне ВС равностороннего треугольника АВС отмечена точка D. O₁ и О₂ – соответственно центры описанных около треугольников ABD и ACD окружностей, а I₁ и I₂ – соответственно центры вписанных в эти же треугольники окружностей. Докажите, что O₁I₂=O₂I₁.

Доказательство: Радиусы описанных окружностей этих треугольников равны между собой, т.к. согласно теореме синусов равны R=АD/2sin60°. Докажем, что точка I₂ лежит 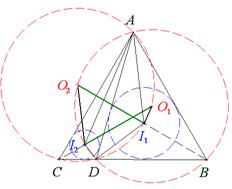на первой из описанных окружностей, а I₁ – на второй. Заметим, что ÐAI₂D=180°–(ÐI₂AD+ÐI₂DA)=180°–(ÐCAD+ÐCDA)/2=180°–(180°–ÐACD)/2=180°–(180°–60°)/2 =120°. Тогда ÐAI₂D+ÐABD=120°+60°=180°, значит, с учётом расположения точек I₂ и В по разные стороны от прямой AD получаем, что ABDI₂ – вписанный четырёхугольник, т.е. точка I₂ лежит на описанной окружности треугольника ABD. Значит, O₁I₂=R. Аналогично доказываем, что O₂I₁=R. Отсюда получаем, что O₁I₂=O₂I₁.

5. На шахматной доске стоят 64 ладьи, по 2 штуки каждого из 32-х цветов. Докажите, что можно убрать 56 ладей и оставить на доске ровно 8 ладей 8-ми различных цветов так, чтобы ладьи не били друг друга.

Решение:Будем считать, что цвета пронумерованы, а на каждой клетке написан номер цвета ладьи, занимающей эту клетку.Известно, что на шахматную доску 8´8 можно поставить 8 ладей, не бьющих друг друга, 8!=8×7×6×5×4×3×2×1=40320 способами, так как в первую вертикаль ладью можно поставить 8-ю способами, во вторую – уже 7-ю и т.д. в последнюю – 1-м способом. А теперь посмотрим, сколько из этих расстановок нам могут не подойти. Расстановка не подходит, если какие-то две ладьи оказались на клетках с одним и тем же числом (номером цвета от 1 до 32). При этом если эти одинаковые числа оказались в одном ряду, то они нам не «портят» ни одного способа. А вот если занятые ими две клетки оказались в разных строках и столбцах, то они как бы «портят» нам 6!=120 способов, потому что оставшиеся 6 ладей размещаются на «доске 6´6», получающейся выбрасыванием по паре соответствующих строк и столбцов. Таким образом, каждый из 32 цветов-чисел может нам «испортить» 0 или 6! способов расстановки 8 ладей, при этом какие-то способы могут быть «испорчены» сразу несколькими разными числами. Но в любом случае в сумме мы теряем не более 32∙6!=23040 способов. Значит, существует не менее 40320–23040=17280 способов расстановки на доске 8 ладей, не бьющих друг друга, при которых ладьи встают на 8 различных числах, т.е. это 8 ладей 8-ми различных цветов, не бьющие друг друга.

Класс

1. Верно ли, что если [[a+b]+c]=a+b+c, то все три числа a, b и c – целые? ([x] – целая часть числа x – наибольшее целое число, не превосходящее x)

Ответ: неверно, например, при a=b=0,5 и с=0 равенство выполняется, но при этом a и b не являются целыми.

2. При каких значениях параметра p система неравенств 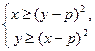имеет единственное решение?

Ответ: p= –1/4. Решение: Если (x₀, y₀) – решение системы, то (y₀, x₀) – тоже решение системы, значит, x₀=y₀. Тогда решаем квадратное неравенство x³(x–p)², дискриминант которого равен D=4p+1, значит, единственное решение система будет иметь только в случае D=0, т.е. при p= –1/4.

В виде суммы какого наименьшего количества точных квадратов можно представить число 2010?

Ответ: 3 квадрата, например, 44²+7²+5²=1936+49+25=2010.Доказательство оценки: 2010 не является точным квадратом, т.к. делится на 3, но не делится на 3²=9, значит, надо взять не менее двух чисел. Предположим, можно взять ровно два числа. Т.к. при делении на 3 квадрат имеет остаток 0 или 1, а сумма этих двух чисел (2010) делится на 3, то и каждый из двух квадратов должен иметь остаток 0. Значит, каждое число делится на 3, следовательно, их квадраты делятся на 9 и вся сумма должна делиться на 9. Но 2010 не делится на 9 – противоречие. Значит, для представления числа 2010 надо взять не менее трёх точных квадратов.

4. ABCD – параллелограмм с ÐA=60°, BDE – равносторонний треугольник, причём точки C и E лежат по одну сторону от прямой BD. Докажите, что треугольник AСE – равнобедренный.

Доказательство: Т.к. ÐBCD=ÐBED=60° и точки С и Е лежат по одну сторону от прямой BD, то точки B, D, C и E лежат на одной окружности (с центром в точке О). Рассмотрим систему координат, в которой точка O – начало координат, точка Е имеет координаты (1; 0). Тогда середина M стороны BD равностороннего треугольника BDE имеет координаты 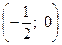. Координаты точки С можно ввести как (cosa; sina), где a=ÐEOC. Значит, координаты вершины A параллелограмма ABCD равны (–1–cosa; –sina) и тогда 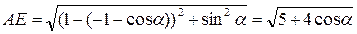, , 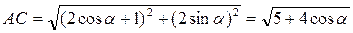т.е. AE=AC.

5. На каком наименьшем квадратном клетчатом поле можно расставить полный комплект кораблей для игры в «морской бой» (1 корабль 1´4, 2 корабля 1´3, 3 корабля 1´2 и 4 корабля 1´1), если корабли могут соприкасаться между собой только вершинами и не могут соприкасаться сторонами?

Ответ: 7´7. Пример расстановки для доски 7´7 на рис. Доказательство оценки: Предположим, что нам удалось разместить корабли на меньшем поле, значит, мы сможем их разместить и на поле 6´6. Разобьём поле 6´6 на 9 квадратов 2´2. В каждом таком квадрате могут находиться максимум две клетки кораблей, иначе корабли будут касаться друг друга сторонами. Значит, на поле может быть не более 9×2=18 клеток всех кораблей. А всего корабли вместе содержат 4+2×3+3×2+4×1=20>18 клеток. Противоречие. Значит, разместить корабли можно только на поле размера не меньше 7´7. А на этом поле их можно разместить даже без соприкосновения – см. рис.

11 класс

1. При каких значениях параметра a уравнениеx²+y²+z²+t²+a=x+y+z+t имеет единственное решение?

Ответ: при a=1. Решение: Перенесём всё в одну сторону и выделим сумму четырёх полных квадратов (x-1/2)²+(y-1/2)²+(z-1/2)²+(t-1/2)²+a-1=0, откуда и следует, что при a>1- решений у уравнения нет, при a=1- решение единственное - все числа равны 1/2, при a<1 - решений бесконечно много.

2. В ряд выписаны все натуральные числа от 1 до 11 и в 10 промежутках между ними расставляются произвольным образом знаки + и -. Какое наименьшее положительное значение может принимать полученное числовое выражение?

Ответ: 2. Доказательство: Т.к. в данной целочисленной знакопеременной сумме будет чётное (6) количество нечётных слагаемых, то вся сумма будет чётной. Значит, минимальное положительное значение, которое она может принимать, равно 2. При этом значение 2 можно получить, например, расставив знаки следующим образом: 1-2+3-4-5-6-7-8+9+10+11=34-32=2.

Комментарий: фактически это задача С6 с ЕГЭ-2010. И на нашу олимпиаду поставлена для проверки, как готовятся нынешние одиннадцатиклассники к ЕГЭ-2011, а также для сравнения результатов одиннадцатиклассников и девятиклассников.

3. Докажите, что в любом натуральном числе, не меньшем 1000 и не делящемся на 3, можно зачеркнуть несколько (возможно одну) цифр так, что оставшееся число будет меньше 1000 и разделится на 3.

Доказательство: 1). Если в числе есть цифра, кратная 3, то оставим только её и получим однозначное число (возможно 0), делящееся на 3. 2). Если в числе нет цифры, кратной 3, но есть цифры с разными остатками (1 и 2) при делении на 3, то оставим только их, тогда сумма цифр получившегося двузначного числа будет кратна 3, значит, и само число разделится на 3 согласно признаку делимости на 3. 3). Если в числе все цифры с одинаковым остатком при делении на 3 (а их при этом не меньше 4-х, т.к. число не меньше 1000), то оставим ровно 3 цифры с одинаковым остатком при делении на 3, тогда получившееся трёхзначное число будет делиться на 3.

4. Какие значения может принимать двугранный угол a при основании правильной треугольной пирамиды, если уравнение x²+x×sina+cosa=0 имеет действительные корни?

Ответ: 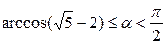. Решение: Т.к. уравнение имеет корни, то его дискриминант D₁=sin²a-4cosa³0. Отсюда 1-cos²a-4cosa³0 и получаем квадратное относительно cosa неравенство cos²a+4cosa-1£0. Его дискриминант D₂=16+4=20>0, старший коэффициент 1>0, значит, данное неравенство выполняется, если cosa лежит между корнями квадратного трёхчлена 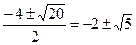. Учитываем также, что двугранный угол при основании правильной треугольной пирамиды будет острым, значит, угол a удовлетворяет неравенству 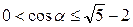, при этом 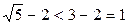. Следовательно, .

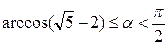Комментарий: это задача-пародия – задача «ни о чём» в стиле ЕГЭ. Чтобы её решить, надо просто нормально знать весь школьный курс математики.

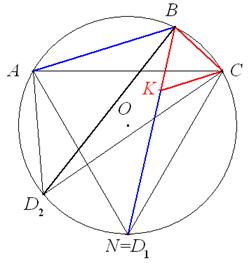5. ABCD – вписанный четырёхугольник, у которого ÐАВС=120° и АВ+ВС=BD. Найдите ÐACD, если известно что ÐВАС=a.

Ответ: 60° и 2a, в частности, при a=30° ответом является только 60°. Решение: На биссектрисе ÐАВС, пересекающей описанную окружность четырёхугольника в точке N, отметим точку К такую, что ВК=ВС, тогда равнобедренный DВКС окажется и равносторонним, т.к. ÐКВС=120°/2=60°. Тогда из равенств ÐАВС=120°=ÐNKC (внешний угол равностороннего треугольника), ÐВАС=ÐBNC (вписанные углы, опирающиеся на одну дугу) и BC=KC следует равенство треугольников АВС и NKC, значит, BN=BK+KN=BC+BA=BD, т.е. точка N является одним из возможных вариантов расположения точки D. Окружность с центром В и радиусом BN=АВ+ВС может пересекать описанную окружность четырёхугольника либо в одной точке (в случае, если АВ=ВС и ABCN окажется дельтоидом), либо в двух точках. При этом ÐACN=ÐABN=60° (вписанные углы, опирающиеся на одну дугу), значит, в первом случае и для одной из точек (D₁) второго случая нужный нам ÐACD=60°. Для второго положения точки (D₂) во втором случае (на чертеже рассматриваем один из двух симметричных случаев: АВ>ВС, т.е. точка D₂ лежит внутри меньшей дуги AD₁, равной 120°) получаем, что с учётом равнобедренности DBD₁D₂ и опоры на равные дуги ÐACD₂=ÐBСD₂-ÐBCA=ÐBD₁D₂-ÐBCA= =ÐBD₂D₁-ÐBCA=ÐBAD₁-ÐBCA=ÐBAC+ÐCAD₁-ÐBCA=a+60°-(180°-ÐABC-ÐBAC)= =a+60°-(60°-a)=2a.

6. Про действительные числа a, b и c известно, что a²+b=b²+c=c²+a. Верно ли, что все эти три числа равны между собой?

Ответ: неверно, например, равенство выполняется для набора из трёх различных чисел a=1, b=t²>1 и c=t, где t – отрицательный корень многочлена f(x)=x³+x²+1 на интервале (-2; -1). Доказательство: Заметим, что f(-2)= -3<0, f(-1)=1>0, значит, на интервале (-2; -1) наш многочлен действительно имеет корень, который и назовём t. Подставим вместо a, b и c соответственно значения 1, t² и t, которые между собой не равны. Получим, что должно выполняться условие: 1+t²=t⁴+t=t²+1. Это условие действительно выполняется, т.к. оно равносильно равенству t⁴-t²+t-1=0, которое верно в силу равенства t⁴-t²+t-1=(t-1)(t³+t²+1)=0, выполняющегося при отрицательном корне t многочлена f(x)=x³+x²+1 на интервале (-2; -1).

Решение 2:неверно, например, равенству удовлетворяет тройка чисел 7/4, -5/4, 1/4.