Моменты инерции простейших сечений
Для простейших сечений моменты инерции определяют методом непосредственного интегрирования. Рассмотрим некоторые примеры решения задач по определению моментов инерции простейших фигур:
 а) Прямоугольник с размерами b
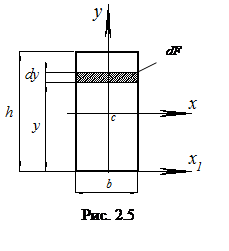
а) Прямоугольник с размерами b 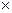 h (рис. 2.5). Для решения задачи воспользуемся формулами (2.5). Выберем вспомогательную ось
h (рис. 2.5). Для решения задачи воспользуемся формулами (2.5). Выберем вспомогательную ось 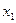 . На расстоянии у от оси х1 выделим элементарную площадку dF=bdy. Подставляя площадь элементарной площадки dF в формулу (2.5), определим осевой момент инерции относительно оси х1:
. На расстоянии у от оси х1 выделим элементарную площадку dF=bdy. Подставляя площадь элементарной площадки dF в формулу (2.5), определим осевой момент инерции относительно оси х1:
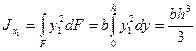
Теперь найдем момент инерции относительно оси х, применяя первую из формул (2.13):
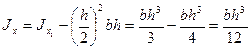 (2.14)
(2.14)
Аналогично можно найти осевой момент инерции относительно оси у:
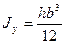
б) Треугольник с основанием b, высотой h (рис. 2.3). Выделенную элементарную площадь dF подставим в формулу (2.5). Получаем значение момента инерции относительно оси х1:
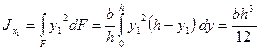 .
.
Момент инерции относительно оси х, параллельной данной оси х1, найдем по первой формуле (2.13):
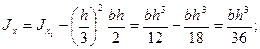
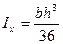 (2.14*)
(2.14*)
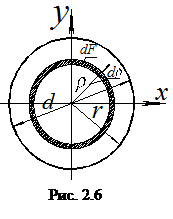
в) Круградиусом r (диаметром d) (рис. 2.6). Найдем сначала полярный (2.7) момент инерции по формуле:
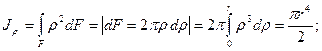
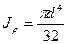 (2.15)
(2.15)
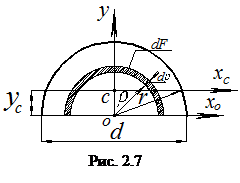 г) Полукруг радиусом r =d/2 (рис.2.7). Приведем без вывода формулы для определения координаты центра тяжести ус полукруга и вычисления моментов инерции относительно главных центральных осей х и у
г) Полукруг радиусом r =d/2 (рис.2.7). Приведем без вывода формулы для определения координаты центра тяжести ус полукруга и вычисления моментов инерции относительно главных центральных осей х и у
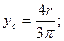
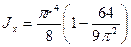 ; (2.16)
; (2.16)
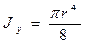
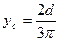
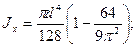 (2.17)
(2.17)
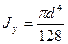 ;
;
Обучающемуся рекомендуется получить приведенные ответы решений самостоятельно, пользуясь (рис. 2.7).
Зависимость между моментами инерции при повороте осей координат
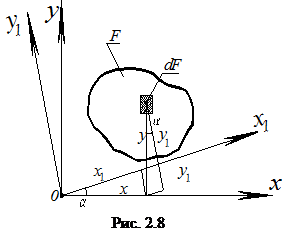 Пусть известны значения моментов инерции Jx, Jy, Jxy, относительно системы координат х и у. (рис.2.8). Повернем оси х и у в новое положение х1 и у1 на угол α против часовой стрелки относительно общего начала.
Пусть известны значения моментов инерции Jx, Jy, Jxy, относительно системы координат х и у. (рис.2.8). Повернем оси х и у в новое положение х1 и у1 на угол α против часовой стрелки относительно общего начала.
Требуется определить значения моментов инерции относительно новой системы координат х1 и у1. Как видно по рис 2.8, зависимости между координатами центра тяжести элементарной площадки dF для новой и исходной систем координатных осей, будут такими.
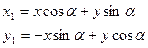 (а)
(а)
Выражения (2.5) и (2.6) для моментов инерции относительно осей х1 , у1 можно представить таким образом
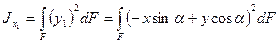 :
:
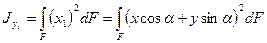
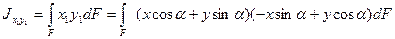 .
.
После раскрытия скобок и учитывая, что интеграл суммы равен сумме интегралов, также зависимости (2.5) и (2.6) относительно исходных осей, получаем:
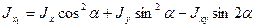 (2.18)
(2.18)
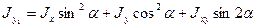 (2.19)
(2.19)
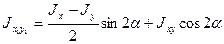 (2.20)
(2.20)
Пользуясь формулами (2.18), (2.19), 2.20), можно определять значения моментов инерции относительно любой пары взаимно перпендикулярных осей х1 и у1, повернутых относительно осей х и у на угол α в положительном направлении, т.е. против часовой стрелки.
Складывая (2.18) и (2.19), получаем
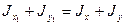 , (б)
, (б)
т.е. сумма осевых моментов инерции относительно взаимно перпендикулярных осей есть величина постоянная.
