Проверка прочности балок при изгибе

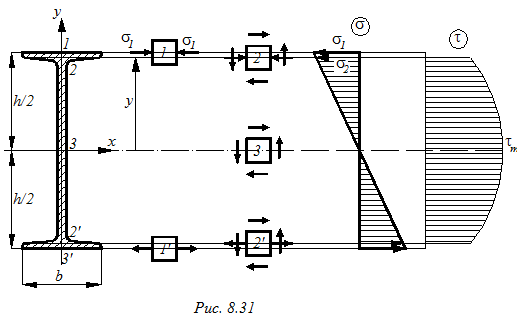Проверку прочности балок при изгибе рассмотрим на примере двутаврового поперечного сечения (рис.8.31). Поперечные размеры балки определяют из условия прочности по максимальным нормальным напряжениям, которые возникают в зоне верхних и нижних волокон балки, элементы 1 и 1^I. После этого принятое сечение проверяют по действию нормальных и касательных напряжений. Максимальные касательные напряжения возникают в точках, расположенных на нейтральной линии поперечного сечения, элемент 3 (рис. 8.31).

τ_max = 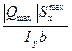≤ R_cp

Для двутаврового поперечного сечения на уровне 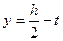расположен элемент 2, на который одновременно действуют достаточно большие нормальные и касательные напряжения. Прочность этого элемента, который находится в состоянии плоского напряженного состояния, проверяется по главным напряжениям по третьей или четвертой теории прочности:

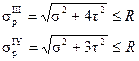
Для проверки прочности балки по главным напряжениям из эпюр М_х и Q_y находят такое сечение по длине балки, в котором действуют достаточно большие изгибающие моменты и поперечные силы. Для двутаврового сечения по высоте балки опасной является точка, которая находится на стыке полки и стенки. Балки по главным напряжениям проверяются в том случае загружения, когда на небольших расстояниях друг от друга приложены большие сосредоточенные силы.

Пример №8.8.

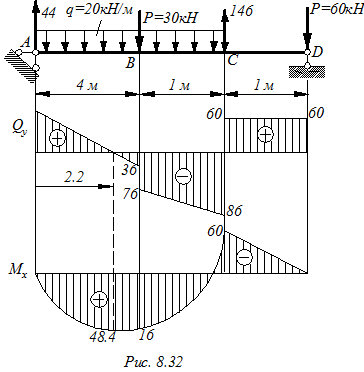Для балки, показанной на (рис.8.32), подобрать двутавровое поперечное сечение. Выполнить полную проверку прочности принятого двутаврового сечения. Расчетное сопротивление материала балки принять R=200 МПа.

Максимальный момент по длине балки возникает в сечении С–М_max=60КНм. Подбираем необходимый двутавр:

W_x= 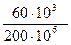=300·10^-6 = 300 см³

этому моменту сопротивления соответствует двутавр

№24А – I_x=3800 см⁴, 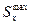=178 см³; t = 0,98 см; d=0,56с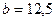м; cм;

W_x = 316,7 см³.

1. Проверяем прочность принятого двутавра по максимальным нормальным напряжениям

σ_max = 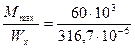=189,5·10⁶ = 189,5 МПа

2. Проверяем прочность двутавра по касательным напряжениям –Q_max=86 кН.

τ_max = 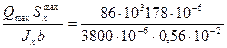=71,9 МПа< 140 МПа

3. Проверяем прочность балки по третьей теории прочности. Опасное сечение расположено бесконечно близко слева от точки С: М_х=60 кНм, Q_y=60кН.

Проверку делаем для точки 2, расположенной на стыке полки и стенки двутавра:

σ₂ = 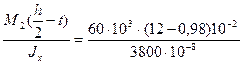= 174 МПа

τ₂ = 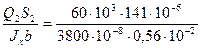= 39,75 МПа

Здесь S₂ = 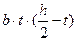=12,5·0,98·(12 – 0,49) = 141 см³.

Результирующее напряжение по третьей теории прочности

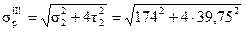=192 МПа < 200МПа.

ЛИТЕРАТУРА

1. Дарков А.В., Шпиро Г.С. Сопротивление материалов. М.; Высш. шк., 1969.

2. Кисилев В. А. Строительная механика. Специальный курс (Динамика и устойчивость сооружений). –М.: Из-во лит. По строительству, 1964. –331 с.

3. Писаренко Г. С., Квітка О. Л., Уманський Е. С. Опір матеріалів.-К.: Вища шк. , 1993. 665 с.

4. Писаренко Г. С. и др. Сопротивление материалов. :Высш. шк., 1986.-775 с

5. Смирнов А.Ф. Сопротивление материалов. -М.; Высш. шк., 1975.-479 с.

6. Тимошенко С.П., Дж. Гере. Механика материалов. - М.: Мир,1976.- 670с.

7. Феодосьев В. И Сопротивление материалов. .-М.; Наука., 1986.-512 с.

8. Шевченко Ф. Л. Изгиб стержневых систем: Учеб. Пособие.-Донецк:ДПИ,1984.-95 с.

9. Шевченко Ф. Л. Механика упругих деформируемых систем. Часть 1,Напряженно деформированное состояние стержней. Учеб. пособие.-Киев,1993 279 с.

10. Шевченко Ф. Л. Механика упругих деформируемых систем. Часть 2,Сложное напряженное состояние Учеб. пособие.-Киев,1993 239 с.

11. Шевченко Ф. Л. Механика упругих деформируемых систем. Часть 3. Учеб. пособие.-Киев. УМК ВО,1993 95 с.

12. Тимошенко С.П. Колебания в инженерном деле. – М.: Наука, 1967. –442с.