В проекциях на оси координат условия равновесия, представляются в виде

Для системы сил, лежащей в плоскости xОy, последнее уравнение удовлетворяется тождественно. Если равнодействующая определена с помощью силового многоугольника, то условием равновесия сходящихся сил является его замкнутость, т.е. для равновесия системы сил необходимо чтобы конец силы совпал с началом силы .

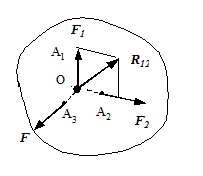Теорема о трех силах. Теорема. Если плоская система трех непараллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.

Доказательство. Пусть система трех сходящихся сил 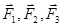находится в равновесии (рис. 10). Предположим, что силы приложены в точках А_1, A₂, A₃, а линии действия сил 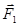и 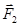пересекаются в точке О. Перенесем силы и 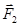по линиям их действия в точку О и по правилу параллелограмма найдем их равнодействующую 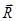. Тогда

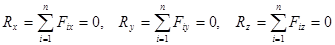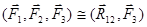Но система двух сил, согласно аксиоме 1, находится в равновесии только в том случае, если эти силы направлены по одной прямой. Следовательно, линия действия силы 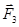должна совпадать с линией действия силы 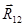. Поскольку линия действия силы 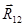проходит через точку О, то и линия действия силы 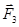проходит через точку О. Что и требовалось доказать.

Эта теорема используется при решении задач на равновесие тел, находящихся под действием плоской системы трех сил,

Пример. Земляная насыпь подпирается вертикальной каменной стеной АВ. Найти необходимую толщину стены 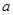, предполагая, что давление земли на стену направлено горизонтально, приложено на 1/3 ее высоты и равно 60 кН/м (на метр длины стены), удельный вес кладки 20 кН/м³.(Cтена должна быть рассчитана на опрокидывание вокруг ребра А).

Расчет плоских ферм.Пример решения задач на равновесие тел дает расчет ферм. Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферму называют плоской. Места соединения стержней фермы называют узлами.Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложенные к его концам, которые при равновесии могут быть

направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Мы будем рассматривать жесткие плоские фермы, образованные из треугольников. В таких фермах число стержней k и число узлов 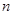связаны соотношением 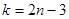. В самом деле, в треугольнике, образованном из трех стержней, будет три узла. Присоединение каждого следующего узла требует два стержня. Следовательно, для всех остальных 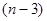узлов потребуется 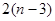стержней. В результате в ферме будет число стержней 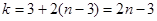. При меньшем числе стержней ферма не будет жесткой, а при большем числе она будет статически неопределимой.

Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях.

Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело.

Для определения усилий в стержнях рассмотрим два способа.

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов. Ход расчетов поясним на конкретном примере.

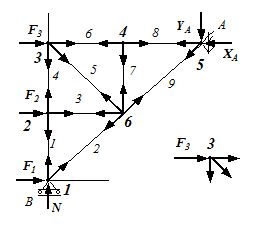
Рассмотрим изображенную на рисунке ферму, образованную из одинаковых равнобедренных прямоугольных треугольников. Действующие на ферму силы параллельны оси х и численно равны 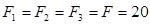кН. В этой ферме число узлов 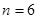, а число стержней 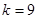. Следовательно, необходимое соотношение выполняется и ферма является жесткой без лишних стержней.

Составляя уравнения равновесия для фермы в целом, найдем, что реакции опор направлены, как показано на рисунке, и численно равны: .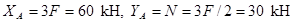

Определим теперь усилия в стержнях. Пронумеруем узлы фермы. Искомые усилия в стержнях обозначим 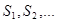. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от остальной фермы. Действие отброшенных стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям 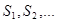. Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растянутыми. Изображенную картину надо представить себе для каждого узла так, как это показано на рисунке. Если в результате расчета значения усилия в каком-нибудь стержне получится отрицательным, это будет означать, что данный стержень не растянут, а сжат.

Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия. Для каждого узла мы можем составить два уравнения равновесия. Поэтому число неизвестных усилий, входящих в эти уравнения не должно быть больше двух. (Заметим, что если в узле сходятся только два стержня и к узлу не приложена ни активная сила, ни реакция опоры, то усилия в стержнях, сходящихся в этом узле равны нулю). В нашей ферме этому условию удовлетворяют узлы 1 и 6. Начнем расчет с узла 1. Составим для него два уравнения равновесия:

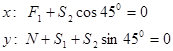Отсюда находим:

Теперь, зная 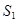, переходим к узлу 2. Для него уравнения равновесия дают: 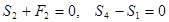, откуда .

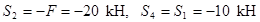Определив , составляем аналогичным путем уравнения равновесия сначала для узла 4, затем для узла 5. Из этих уравнений находим: .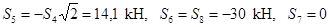

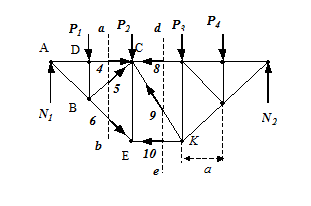
Наконец, для вычисления 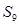достаточно составить одно уравнение равновесия сил, сходящихся в узле 6, в проекциях на ось у. Получим 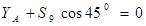, откуда .

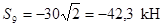Как показывают знаки усилий, стержень 5 растянут,остальные стержни сжаты, стержень 7 не нагружен.

Если в ходе расчета встретится узел, для которых число неизвестных больше двух, то можно воспользоваться методом сечений.

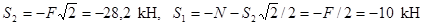Метод сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуются определить усилия, и рассматривают равновесиеодной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни растянутыми (как и в методе вырезания узлов). Затем составляют уравнения равновесия по второй или по третьей форме условий равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

Пример.Пусть требуется определить усилие в стержне 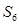фермы, изображенной на рисунке. Действующие вертикальные силы 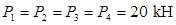, реакции опор 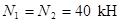. Проведем сечение 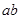через стержни 4,5,6 и рассмотримравновесие левой части фермы, заменяя действие на нее правой части силами, направленными вдоль стержней 4,5,6. Чтобы найти 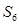составим уравнение моментов относительно точки С, где пересекаются стержни 4 и 5. Получим, считая ,

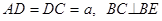Отсюда находим 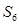. Плечо СВ вычисляем по данным, определяющим направления и размеры стержней фермы.

В данном примере 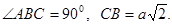Следовательно, 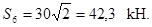Стержень растянут.

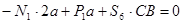Усилия в стержнях 4 и 5 можно найти, составляя уравнения моментов относительно центров В (точка пересечения стержней 5 и 6) и А (точка пересечения стержней 4 и 6).

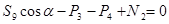Чтобы определить усилие в стержне 9 той же фермы, проводим сечение 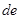через стержни 8, 9 и 10. Получим

откуда находим 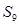. Усилия в стержнях 8 и10 можно в этом случае найти, составив уравнения моментов относительно центров К и С.

Примеры.

Пример 1. К веревке AD, один конец которой закреплен в точке A, привязаны в точке D груз P и веревка BCD, перекинутая через блок; к концу ее привязана гиря Q весом 10 кН. Определить, пренебрегая трением в блоке, натяжение T веревки и вес груза P, если углы, образуемые веревками с вертикалью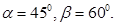

Решение. Рассмотрим равновесие узла B. Этот узел находится в равновесии под действием активной силы 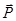и реакций нитей 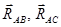, причем 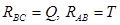(рис. 12). Выбирая начало системы координат в точке B, получим систему сил, представленную на рис.13. Cоставляя уравнения равновесия, получим

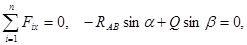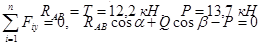Подставляя сюда вместо 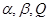их численные значения и решая систему уравнений, находим

Пример 2. На двух взаимно перпендикулярных гладких наклонных плоскостях AB и BC лежит однородный шар весом P=6 кН. Определить давление шара на каждую из плоскостей, считая, что плоскость составляет с горизонтом угол 60⁰

Решение. Составим уравнения равновесия, (рис. 15):

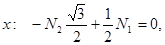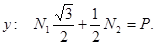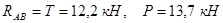Отсюда находим, что

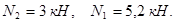
Пример 3. Определить реакции опор и усилия в четырех невесомых стержнях плоской фермы (рис. 16).

Дано: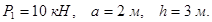

Решение. 1. Определим реакции опор. Линии действия двух сил 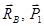известны. По теореме о трех силах линия действия реакции 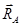, неподвижного шарнира проходит через точку A и точку пересечения линий действия сил 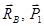. Из 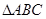находим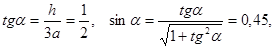

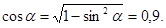
Уравнение равновесия данной системы сил имеют вид

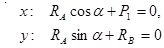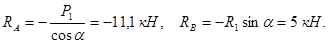Отсюда получим

Так как модуль реакции 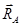отрицательный, то реакция 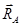направлена противоположно показанной на рисунке.

2.

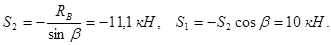Определим усилия в стержнях 1, 2, 3, 4. Для этого вырежем (мысленно) сначала узел В, где соединены два стержня, 1 и 2. К узлу B приложим реакции стержней 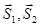а также известную реакцию 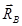. Предположим, что оба стержня растянуты, т.е. усилия 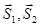, приложенные к узлу, направлены от узла B вдоль стержней, рис. 17. Из уравнений равновесия узла B получим

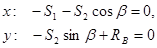где 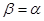(рис. 16). Отсюда находим

Отрицательный знак модуля усилия 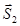означает, что эта сила направлена к узлу, т.е. стержень 2 сжат. Стержень 1 растянут.

Вырежем теперь узел D. Усилие 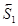в первом стержне найдено и, следовательно, неизвестны теперь модули двух усилий в стержнях 3 и 4, 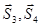,. Приложим к узлу реакции отрезанных стержней 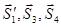, предполагая их растянутыми, т.е. направленными от узла D, (рис. 18). При этом .

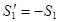Из уравнений равновесия узла D имеем:

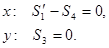Следовательно 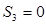, (3-ий стержень нулевой), 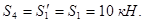(4-й стержень растянут).

Проверим решение графическим методом. Построим в масштабе замкнутые силовые треугольники для узлов и, в каждом по известной силе и известным линиям действия двух сил, рис. 19, 20. Из этих треугольников следуют те же результаты, которые получены аналитическим методом.

Пример 4. Определить усилия в невесомых стержнях пространственной фермы, состоящей из шести невесомых стержней. Стержни соединены в узлах и с опорами в вершинах прямоугольного параллелепипеда шарнирами как показано на рис. 21.

В прямоугольном параллелепипеде ABCOKEDL с ребром параллельным оси z равным a=3 м имеем уголы: 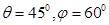. Углы, составленные силами 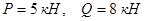c осями x,y,z, соответственно, указаны в скобках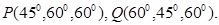

Решение. Из 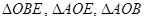имеем

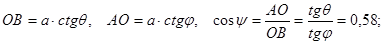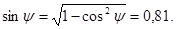Вырежем узел B и заменим отрезанные стержни их реакциями, предполагая эти стержни растянутыми. Составим уравнения равновесия для узла B, в котором соединены три стержня.

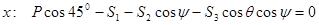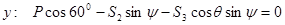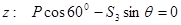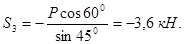Отсюда

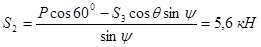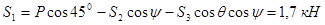Таким образом, стержни 1, 2 растянуты, стержень 3 сжат.

Вырежем теперь узел E . Заменим отрезанные стержни их реакциями, предполагая стержни растянутыми. При этом модули реакций стержня 3 в узлах B и E равны 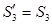, Уравнения равновесия узла E:

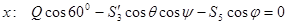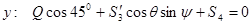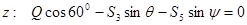Отсюда

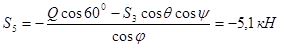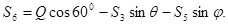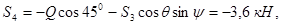Следовательно, стержни 4 и 5 сжаты, стержень 6 растянут.