Для вычисления интеграла используем

,

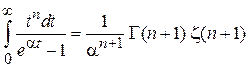Получаем

, (4.57а)

где z(3) = 1,202, тогда

,

. (4.58)

Среднее число фотонов пропорционально объему полости и третьей степени температуры стенок. При находим . Эти фотоны поддерживают тепловое равновесие тел, находящихся в полости.

Реликтовое излучение (от лат. reliquiae – «остатки») испущено при образовании Вселенной в результате «большого взрыва», произошедшего 13,7·10⁹ лет тому назад. Возник шар огня радиусом R. По мере расширения шара со скоростью света температура и энергия фотонов уменьшалась, по прошествии 400·10³ лет температура стала порядка 3000 К. При такой температуре притяжение протонов и электронов объединило их в атомы водорода с нулевым электрическим зарядом. Энергии фотонов стало не хватать для ионизации атома водорода. Фотоны перестали интенсивно взаимодействовать с материей. Вселенная стала прозрачной. Число фотонов перестало существенно изменяться, и сохранилось до нашего времени. Из (4.58) находим

,

.

Температура излучения понижается обратно пропорционально увеличению расстояния R между космическими телами. В настоящее время температура реликтовых фотонов

,

тогда согласно (4.58) их средняя концентрация

.

Реликтовое излучение предсказал Георгий Гамов на основе горячей модели Вселенной, предложенной в 1946 г. В 1956 г. он оценил температуру излучения в 6 К.

Излучение с одинаковой интенсивностью по всем направлениям с температурой обнаружил советский физик Тигран Арамович Шмаонов в 1956 г. Он использовал радиоаппаратуры с рекордной чувствительностью на волне 3,2 см. Статья опубликована в журнале «Приборы и техника эксперимента» в 1957 г. Обнаруженное излучение он объяснил радиоизлучением атмосферы.

Независимо зарегистрировали излучение на волне 7,35 см британцы Арно Пензиас и Роберт Вильсон в 1965 г. Им дали Нобелевскую премию 1978 г.

Термин «реликтовое излучение», от лат. «остатки», ввел советский астрофизик Иосиф Самуилович Шкловский, поскольку это излучение отражает состояние Вселенной на ранних этапах эволюции. Спектральный анализ реликтового излучения и его зависимость от направления позволили измерить направление и скорость движения солнечной системы относительно собственной системы отсчета большого взрыва. Также получен закон изменения скорости разбегания галактик с течение времени.

Спектральная плотность излучения. Используя (4.53) и (4.57)

,

,

получаем формулу Планка (1900 г.) для энергии единицы объема фотонного газа в интервале частот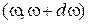

. (4.59)

Спектральная плотность энергии – энергия единицы объема полости в единичном интервале частот около w

,

равна

. (4.60)

При низкой частоте 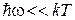из (4.60) получаем

.

При высокой частоте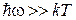

.

Положение экстремума спектральной плотности находим из условия

.

Для переменной из (4.60) получаем

.

Приходим к уравнению

.

Решение дает закон смещения Вина

,

, (4.61)

установленный Вильгельмом Вином в 1893 г. При изменении температуры максимум спектральной плотности излучения сдвигается пропорционально температуре. Например, при максимум находится в желто-зеленом участке спектра. Подставляя (4.61) в (4.60), получаем

,

. (4.62)

С ростом температуры максимум спектральной плотности излучения увеличивается пропорционально кубу температуры.

Плотность энергии излучения со всеми частотами находим из (4.59)

.

Используя

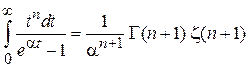
находим интеграл

.

Получаем закон Стефана–Больцмана для энергии единицы объема полости с температурой Т

, (4.63)

где

.

Результат получил экспериментально Йозеф Стефан в 1879 г. и теоретически Людвиг Больцман в 1884 г. Из (4.63) следует, что площадь под кривой спектральной плотности энергии пропорциональна четвертой степени температуры.

Внутренняя энергия, или энергия излучения в полости объемом V, получаем из (4.63)

. (4.63а)

Средняя энергия, приходящаяся на один фотон . Используем среднюю энергию единицы объема (4.63) и концентрацию фотонов (4.58)

.

Получаем

. (4.64)

Для частицы классического газа .

Свободная энергия. Используем внутреннюю энергию (4.63а) и уравнение Гиббса–Гельмгольца (2.29)

.

Находим

. (4.65)

Энтропия. Используя (2.33)

,

и (4.65), получаем

. (4.66)

В последнем равенстве учтено (4.58)

,

и (4.63)

.

Энтропия, приходящаяся на один фотон:

, (4.66а)

не зависит от температуры.

Давление. Используем (2.33)

и (4.65)

.

Получаем давление фотонного газа на абсолютно поглощающую стенку

, (4.67)

где использовано и (4.64) . Давление равно одной трети от внутренней энергии единицы объема полости. Для классического газа .

Термодинамический потенциал Гиббса находим из (2.64)

.

Подставляем (4.65)

и (4.67)

,

получаем

.

Из (2.66)

следует, что химический потенциал фотона равен нулю. Это согласуется с (4.55).

Адиабатический процесс, происходящий с изменением объема полости, определяется уравнением

.

Из (4.66)

получаем

.

При адиабатическом процессе сохраняется среднее число фотонов.

Выражая Т через Р с помощью (4.67)

,

и учитывая (4.66)

,

при получаем уравнения адиабатического процесса

,

. (4.68)

Изотермический процесс. При изотермическом изменении объема полости с излучением давление (4.67)

сохраняется. Согласно (4.58)

число фотонов пропорционально объему.

Энергетическая светимость R абсолютно черного тела. По определению, R равно энергии, излучаемой единицей площади за единицу времени со всеми частотами и под всеми углами. Если стенка полости абсолютно черная, то она поглощает всю падающую энергию. В состоянии теплового равновесия энергия, излучаемая элементом стенки, равна энергии, падающей на этот элемент. Тогда светимость абсолютно черного тела равна энергии, падающей на единицу площади за единицу времени под всеми углами и со всеми частотами.

За единицу времени на единичную площадку под углом q к нормали падает энергия

,

где u – энергия единицы объема; С – скорость света; – поперечное сечение пучка. Тепловое излучение, находящееся в элементе объема полости, распространяется с равной вероятностью по всем направлениям. В результате

,

где усреднение проводится по всем направлениям падающего пучка

;

– элемент телесного угла в сферических координатах. Угол q изменяется в пределах (0, p/2). Полный телесный угол, в пределах которого распространяется излучение в полости, равен 4p, тогда

.

В результате

.

Используя (4.63) , получаем закон Стефана–Больцмана для светимости абсолютно черного тела

, (П.11.1)

где постоянная Стефана–Больцмана

.

Сила Казимира возникает между двумя параллельными, близко расположенными проводящими пластинами. Сила создается виртуальными фотонами, рождающимися самопроизвольно из вакуума. Такой фотон с энергией и частотой ω появляется на время τ согласно соотношению неопределенностей . В результате появляются электромагнитные волны.

Среднее число тепловых фотонов согласно (4.58)

при низкой температуре мала , и главную роль играют виртуальные фотоны.

Между пластинами возникают стоячие электромагнитные волны с частотами , удовлетворяющими граничным условиям на пластинах. Стоячую волну с частотой ω рассматриваем как линейный осциллятор с энергией . При остается энергия нулевых колебаний . Суммируем по всем волнам, удовлетворяющим граничным условиям, и получаем энергию единицы объема

.

Частоту волны выражаем через волновые числа вдоль ортогональных направлений

,

где волновой вектор k₁ направлен перпендикулярно пластинам. Значения волновых чисел определяются граничными условиями. Считаем пластины квадратными со стороной L, расстояние между пластинами l. Периодические условия означают, что между противоположными границами доступного объема укладывается целое число полуволн, тогда

, , .

Между пластинами множество значений k₁ дискретное. Вне пластин пространство неограниченное и k₁ меняется непрерывно. Следовательно, число мод и плотность энергии ε между пластинами меньше, чем снаружи пластин. Между пластинами исчезает часть виртуальных фотонов. Давление пропорционально плотности энергии. В результате на пластины действует сближающая сила. Чем ближе пластины друг к другу, тем меньше частот удовлетворяют граничным условиям, тем меньше виртуальных фотонов, и меньше энергия и давление между пластинами. Внешнее давление при этом не меняется, поэтому сила увеличивается при сближении пластин. Значения волновых чисел и частот неограниченные, и плотности энергии оказываются бесконечными. Однако, их разность конечная. Производная по l от этой разности энергий дает силу

.

Сжимающая сила Казимира, приходящаяся на единицу площади пластин:

, (П.11.10)

обратно пропорциональна четвертой степени расстояния между пластинами. При получаем Формула применима при .

Подобное явление наблюдали французские моряки 18 века. Когда два корабля при сильном волнении моря и слабом ветре оказывались на расстоянии меньшем 40 метров, то волнение воды между ними уменьшалось, а корабли начинали сближаться. Инструкция по мореплаванию предусматривала специальные меры против такого столкновения судов.

Силу притяжения, вызванную вакуумными флуктуациями электромагнитного поля, обнаружил Хендрик Казимир (1909–2000) в 1948 г. при исследовании коллоидных растворов с примесью частиц микронного размера, между которыми наблюдалось притяжение. Первое экспериментальное подтверждение получено в 1958 г. На малых расстояниях сила Казимира становится главной силой взаимодействия между телами, она зависит от формы и материала тел.

Динамический эффект Казимира состоит в том, что если одно из двух параллельно расположенных зеркал движется ускоренно и его скорость близка к скорости света, то из вакуума рождаются пары реальных фотонов за счет энергии движения зеркала. Эффект теоретически описал Gerald Moore в 1970 г., и экспериментально подтвердил C.M. Wilson в 2011 г.

Фононный газ

Тепловые колебания элементов кристалла вызывают распространение по решетке упругих волн смещений элементов решетки из положений равновесия. Фононы являются квантами энергии упругих волн. Внутри кристалла возникает идеальный газ квазичастиц фононов. Основы квантовой статистической теории кристаллической решетки заложили Альберт Эйнштейн в 1907 г. и Питер Дебай в 1912 г. Название фонон от др.-греч. jώnh – «звук» дал Яков Ильич Френкель в 1932 г.

Акустические и оптические волны в кристалле. Число независимых волн равно числу степеней свободы кристалла. Если в элементарной ячейке находятся r частиц и число ячеек N, то трехмерный кристалл имеет 3rN степеней свободы и число типов волн

,

где исключены 6 степеней свободы, связанные с поступательным и вращательным движением кристалла как целого. Из общего количества 3rN волн выделяются 3N волн, имеющих достаточно малую частоту и называемых акустическими. При их распространении элементарная ячейка колеблется как единое целое и зависимость частоты от волнового числа w = w(k) при малом k близка к линейной. Остальные (3r – 3)N волн имеют высокие частоты, обычно находящиеся в инфракрасной области спектра и называемые оптическими. Они вызывают колебания частиц ячейки друг относительно друга, зависимость w = w(k) оказывается нелинейной. Оптические волны возбуждаются при сравнительно высокой температуре. Далее ограничиваемся акустическими волнами.

Закон дисперсии связывает частоту волны ω и волновое число k. Одномерная неограниченная цепочка одинаковых атомов в стационарном состоянии показана на рисунке черными кружками, находящимися на расстоянии d друг от друга. Результирующая сила, действующая на любой атом со стороны соседних атомов, равна нулю. В возмущенном состоянии (серые кружки) смещение атома n от положения равновесия отличается от смещений соседних атомов. На атом n со стороны атома n + 1 действует упругая сила с проекцией на ось x

,

где b – коэффициент жесткости; – увеличение расстояния между атомами. Учет двух соседних атомов, действующих на атом n в противоположные стороны, дает проекцию результирующей силы

.

Из второго закона Ньютона для атома n получаем уравнение

.

Зависимость смещения атома n от времени ищем в виде бегущей продольной волны

,

где nd – положение атома n; k – волновое число; ω – частота колебаний. Подставляем решение в уравнение, сокращаем одинаковый множитель , и получаем

.

Выражаем частоту через волновое число и находим закон дисперсии

. (П.1)

Разные знаки k соответствуют двум направлениям волны.

Функция синуса ограничена единицей, тогда из (П.1) получаем границы области значений:

частоты колебаний

,

волнового числа

,

длины волны

.

Наличие минимальной длины волны очевидно из физической картины, показанной на рисунка. По цепочке атомов, расположенных на расстоянии d друг от друга, идет поперечная волна. При волны не существует.

При минимальной длине волны получаем смещение атома n

,

в частности:

,

,

.

Следовательно, соседние атомы колеблются в противофазе, как показано на рисунке, бегущая волна превращается в стоячую волну, энергия не переносится по кристаллу.

Для длинных акустических волн

,

из (П.1)

получаем линейный закон дисперсии

. (П.2)

Скорость волны

возрастает с увеличением жесткости кристалла.

Плотность состояний в модели Дебая. Плотность состояний определяется законом дисперсии . Для акустических продольных волн получен линейный закон дисперсии (П.2)

.

В трехмерном кристалле существует три типа упругих волн – один продольный и два поперечных, распространяющихся со скоростями v_m. Для акустических волн используем линейное приближение Дебая

, (П.2.а)

где – модуль импульса для волны типа m. Это соответствует модели кристалла в виде упругого непрерывного тела. Линейное приближение Дебая применимо до частот ~ 10¹³ Гц.

Для линейного закона дисперсии плотность состояний, или число независимых волн в единичном интервале частот равна

, (П.8.10)

где средняя по типам поляризации скорость волн

.

Доказательство (П.8.10). Для волны с частотой ω и типом поляризации i = 1, 2, 3 из (П.2.а) получаем модуль импульса фонона

,

где – скорость волны. Для типа волн , распространяющихся в трехмерном пространстве, аналогично фотонному газу находим

, ,

.

Для числа состояний и плотности состояний получаем

,

.

Аналогичные выражения имеем для типов волн . Состояния независимые, результирующая плотность состояний суммируется

.

Вводя среднюю скорость звука v, получаем

, (П.8.10)

. (П.8.11)

Частота Дебаяw_D равна наибольшей возможной частоте колебаний кристаллической решетки. Ограничение связано с тем, что половина длины волны не может быть меньше расстояния между узлами решетки .

Точное значение w_D получаем из условия – число независимых волн равно числу степеней свободы кристалла. Каждая из N элементарных ячеек совершает колебания по трем независимым направлениям. Тогда число степеней свободы макроскопического кристалла . Выражаем это число через плотность состояний (П.8.10)

.

Находим частоту Дебая

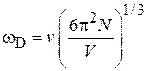. (4.69)

Ячейка кристалла занимает объем

,

где d – постоянная решетки. Из (4.69) получаем

. (4.69а)

Наименьшая длина волны

согласуется с физическим смыслом для волны с частотой Дебая. Из (4.69) выражаем скорость волн через частоту Дебая

,

тогда плотность состояний

получает вид

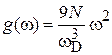. (4.70)

Химический потенциал и функция распределения фононов. По аналогии с фотоном упругой волне с частотой w сопоставляется набор фононов, импульс и энергия которых определяются длиной и частотой волны

, .

Три независимых типа волн в кристалле – одна продольная волна и две поперечных волны, сопоставляем с тремя проекциями спина 1. Следовательно, фононы являются бозонами. Аналогично фотону, фонон не обладает каким-либо сохраняющимся зарядом, поэтому число фононов в кристалле не сохраняется и зависит от температуры. Для равновесного фононного газа

.

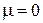Согласно распределению Бозе–Эйнштейна, волне с частотой w соответствует среднее число фононов

.

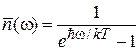Число фононов кристалла в интервале частот равно

.

Тепловая часть внутренней энергии кристалла равна энергии всех фононов

.

Заменяем

, ,

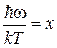находим

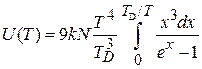, (4.71)

где температура Дебая

.

Температура Дебая соответствует тепловой энергии , равной наибольшей возможной энергии фонона . Используем (4.69а)

,

находим

. (4.72)

Температура Дебая пропорциональна скорости волны v и обратно пропорциональна постоянной решетки d.

В механике известна формула скорости продольных волн

,

где Е – модуль Юнга; r – плотность кристалла. Скорость звука порядка (1…10) км/с и тем больше, чем прочнее вещество. В результате температура Дебая велика для твердых материалов и мала для мягких материалов. Различают прочные и малопрочные кристаллы в зависимости от их температуры Дебая. Границей между ними являются кристаллы с температурой Дебая, близкой к лабораторной температуре.

Крис-талл	C (алмаз)	Be	Si	Fe	Al	Cu	Ag	Au	Na	Pb	Hg
TD, К
энергия фонона , 10–2 эВ	19,2	12,4	5,6	5,0	3,7	3,0	1,9	1,4	1,4	0,9	0,6
	Прочные Малопрочные

Наибольшая энергия фонона гораздо меньше энергии Ферми электрона в металле ~ 4 эВ.