Теоретические основы работы. Теплоемкостью называется количество теплоты, подведенное к системе некоторой массы, увеличивающее температуру этой системы на некоторую величину

Теплоемкостью называется количество теплоты, подведенное к системе некоторой массы, увеличивающее температуру этой системы на некоторую величину. Различают истинную и среднюю теплоемкость, а также молярную и удельную. Истинная теплоемкость – это дифференциально малое количество теплоты, подведенное к системе, увеличивающее температуру этой системы на дифференциально малую величину. Средняя теплоемкость – это количество теплоты, подведенное к системе, увеличивающее температуру этой системы на 1 К. Молярная теплоемкость – это теплоемкость вещества массой 1 моль. Удельная теплоемкость – это теплоемкость вещества массой 1 кг.

Величину теплоемкости можно определить как по справочным данным, так и экспериментальными методами. Одним из таких методов является метод смешения. Метод смешения заключается в том, что два вещества (вода и исследуемое вещество) приводятся в термический контакт. В результате теплообмена система приходит в тепловое равновесие, при котором температуры обоих веществ выравниваются. Если такой процесс провести в калориметрической установке, то к системе применимо уравнение теплового баланса.

Определение теплоемкости вещества осуществляется в две стадии: определение тепловой константы пробирки К (опыт 1) и определение теплоемкости исследуемого вещества (опыт 2).

В опыте 1 в результате теплообмена между нагретой пробиркой и калориметром с водой система приходит в тепловое равновесие, при котором температуры пробирки, калориметра и воды выравниваются. К системе тогда применимо уравнение теплового баланса:

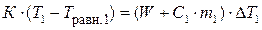, (9)

где К – тепловая константа пробирки для исследуемого вещества, Дж/К; Т₁ – начальная температура пробирки, равная температуре термостата, К; Т_равн.1 – температура пробирки после установления равновесия, К (Т_равн.1= Т₂ + ΔТ₁ (граф)) – температура в калориметре после теплообмена между нагретой пробиркой и водой, К; Т₂ – температура среды, измеренная в конце опыта, К; W - тепловая константа калориметра, Дж/К; С₁ – удельная теплоемкость воды, Дж/(кг∙К); m₁ – масса воды, залитой в калориметр, кг; ΔТ₁ – изменение температуры в результате опыта, найденное графически, К.

В опыте 2 в уравнении теплового баланса учитываются теплоемкость и масса нагретого исследуемого вещества:

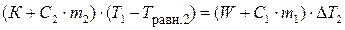, (10)

где С₂ – теплоемкость исследуемого вещества, Дж/(кг∙К); m₂ – масса навески исследуемого вещества, кг; Т_равн.2 – температура пробирки с веществом после установления равновесия, К (Т_равн.2 = Т₃ + ΔТ₂ (граф)) – в калориметре после теплообмена между нагретой пробиркой и водой; Т₃ – температура среды, измеренная в конце опыта, К; ΔТ₂ – изменение температуры в результате теплообмена, найденное графически, К.

Приборы и материалы: термостат, калориметр, термометр Бекмана, мешалка, секундомер, аналитические весы, мерная колба, контейнер (стеклянный сосуд из толстого стекла), дистиллированная вода, исследуемое вещество.

Порядок выполнения работы

1. Получить от преподавателя задание по виду и количеству исследуемого вещества.

2. Включить термостат и нагреть его до Т₁ = 50 ⁰С.

3. Поместить в термостат две одинаковых пробирки, используемых в двух опытах: одну пустую, а другую – с навеской исследуемого вещества на 15-20 мин.

4. Тем временем установить в калориметр термометр Бекмана и мешалку. Залить 60 мл дистиллированной воды комнатной температуры (объем измерить мерным цилиндром).

5. Перемешивая воду, записывать через 1 минуту показания термометра Бекмана в течение 7 – 10 мин до равновесного значения температур. Не прерывая отсчета времени, на 8 – 11 мин от начала опыта поместить в калориметре пробирку, нагретую в термостате. Продолжить отсчет времени еще 10 мин.

6. После окончания отсчетов измерить температуру воды в калориметре обычным термометром Т₂. По результатам опыта построить график изменения температуры и определить графически ΔТ₁.

7. Используя уравнение теплового баланса (9), рассчитать в опыте 1 тепловую константу пробирки.

8. Провести второй опыт с навеской вещества, помещенного во вторую пробирку, в соответствии с пп. 4 и 5. В конце опыта измерить температуру среды Т₃ обычным термометром. По результатам опыта построить график изменения температуры и определить графически ΔТ₂.

9. По результатам опыта рассчитать среднюю теплоемкость исследуемого вещества по уравнению (10).

10. Использовать для расчетов следующие справочные величины:

W = 14,6 Дж/К; С₁ – 4,18∙10³ Дж/(кг∙К).

Контрольные вопросы

1. Что называется теплоемкостью?

2. Что называется истинной и средней теплоемкостью? Как они связаны между собой?

3. Что называется удельной и молярной теплоемкостью?

4. В чем сущность метода смешения?

5. За счет чего устанавливается тепловое равновесие?

6. Для каких целей определяется тепловая константа пробирки?

Химическое равновесие

Теоретическое введение

Химические реакции в большинстве случаев протекают не до конца, а до определенного состояния, называемого химическим равновесием. Химическое равновесие характеризуется следующими общими признаками: неизменяемость системы во времени при неизменных внешних условиях; подвижность равновесия; динамичность равновесия; возможность подхода к состоянию равновесия с двух сторон, минимальное значение энергии Гельмгольца F, энергии Гиббса G и максимальное значение энтропии S системы при постоянстве их естественных переменных.

Применяя к химическим реакциям уравнения, вытекающие из второго закона термодинамики, можно получить очень важные для технологической практики ответы: возможна ли данная реакция; каков будет предельный выход продуктов реакции.

Одной из основных закономерностей в учении о химическом равновесии является закон действия масс.

Рассмотрим в общем виде химическую реакцию, протекающую в разбавленном растворе:

,

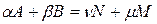где α, β, ν, μ – стехиометрические коэффициенты; А, В, N, М – участники реакции. Тогда закон действия масс запишется так:

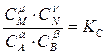, (11)

где К_С − константа равновесия; С_i – равновесные парциальные концентрации участников реакции.

Константа равновесия К_С связывает между собой парциальные концентрации продуктов реакции и исходных веществ в состоянии равновесия химической реакции. При неизменных внешних условиях константа равновесия данной реакции является величиной постоянной.

В зависимости от того, подчиняется или нет изучаемая реакция законам идеальных газов или растворов и в каком агрегатном состоянии находятся участники реакции, в уравнении (11) вместо концентраций будут подставляться равновесные парциальные давления Р_A,B,N,M, активности а_i или летучести f_i участников реакции.

Для реакции, протекающей в газовой фазе и подчиняющейся законам идеальных газов, константа равновесия выражается через равновесные парциальные давления:

,

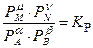где К_Р − константа равновесия; Р_i – равновесные парциальные давления участников реакции.

Константы равновесия К_С и К_Р связаны между собой следующим соотношением:

,

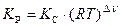где Δν – изменение числа моль газообразных участников реакции.

Изменение энергии Гиббса химической реакции при постоянных давлении и температуре описывается уравнением изотермы химической реакции:

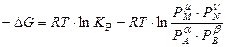, (12)

где ΔG – изменение энергии Гиббса; Р_i –парциальные давления участников реакции для исходного состояния реакции.

Если исходные парциальные давления участников реакции соответствуют стандартным условиям, то уравнение (12) принимает вид:

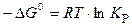, (13)

где 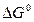− стандартное изменение энергии Гиббса; R – универсальная газовая постоянная, R = 8,314 Дж/(моль∙К).

Уравнение (13) позволяет сравнивать состояние равновесия различных химических реакций при стандартных условиях, рассчитывать по изменению энергии Гиббса константы равновесия, а следовательно, и предельный выход продуктов реакции. Кроме того, уравнение (13) выражает собой стандартное химическое сродство 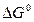реакции.

Константа равновесия зависит от температуры. Эта зависимость математически представляется при постоянном давлении уравнением изобары, а при постоянном объеме – уравнением изохоры реакции.

Уравнение изобары реакции в дифференциальной форме записывается:

,

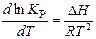где ΔН – изменение энтальпии, или изобарный тепловой эффект реакции.

Интегральные формы этого уравнения:

,

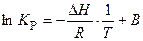где В – постоянная интегрирования;

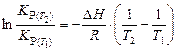. (14)

Здесь 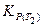− константа равновесия при температуре Т₂; 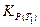− константа равновесия при температуре Т₁.

Зная константы равновесия при двух температурах, по уравнению (14) можно рассчитать изобарный тепловой эффект этой реакции:

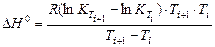, (15)

где R – универсальная газовая постоянная, R = 8,314 Дж/(моль∙К).

РАБОТА 1