Термодинамические потенциалы. Свободная энергия Гиббса и Гельмгольца.

Для характеристики процессов, протекающих в закрытых системах, введем новые термодинамические функции состояния: изобарно-изотермический потенциал (свободная энергия Гиббса G) и изохорно-изотермический потенциал (свободная энергия Гельмгольца F).

Для закрытой системы, в которой осуществляется равновесный процесс при постоянных температуре и объеме, выразим работу данного процесса. Которую обозначим А_max (поскольку работа процесса, проводимого равновесно, максимальна):

A_max=T∆S-∆U

Введем функцию F=U-TS-изохорно-изотермический потенциал, определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях и получим:

∆F=∆U-T∆S

Изменение энергии Гельмгольца определяется только начальным и конечным состоянием системы и не зависит от характера процесса, поскольку оно определяется двумя функциями состояния: U и S. Напомним, что от способа проведения процесса при переходе системы из начального в конечное состояние может зависеть величина полученной или затраченной работы, но не изменение функции.

Закрытую систему, находящуюся в изобарно- изотермических условиях, характеризует изобарно-изотермический потенциал G:

G=U+PV-TS=H-TS

∆G=∆H-T∆S

Дифференциал энергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — через давление p и температуру T:

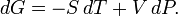
Для системы с переменным числом частиц этот дифференциал записывается так:

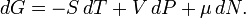
Здесь 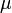— химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу.

Анализ уравнения ∆G=∆H-T∆S позволяет установить, какой из факторов, составляющих энергию Гиббса, ответственен за направление протекания химической реакции, энтальпийный (ΔH) или энтропийный (ΔS · T).

Если ΔH < 0 и ΔS > 0, то всегда ΔG < 0 и реакция возможна при любой температуре.

Если ΔH > 0 и ΔS < 0, то всегда ΔG > 0, и реакция с поглощением теплоты и уменьшением энтропии невозможна ни при каких условиях.

В остальных случаях (ΔH < 0, ΔS < 0 и ΔH > 0, ΔS > 0) знак ΔG зависит от соотношения ΔH и TΔS. Реакция возможна, если она сопровождается уменьшением изобарного потенциала; при комнатной температуре, когда значение T невелико, значение TΔS также невелико, и обычно изменение энтальпии больше TΔS. Поэтому большинство реакций, протекающих при комнатной температуре, экзотермичны. Чем выше температура, тем больше TΔS, и даже эндотермические реакции становятся осуществляемыми.

Под стандартной энергией Гиббса образования ΔG°, понимают изменение энергии Гиббса при реакции образования 1 моль вещества, находящегося в стандартном состоянии. Это определение подразумевает, что стандартная энергия Гиббса образования простого вещества, устойчивого в стандартных условиях, равна нулю.

Изменение энергии Гиббса не зависит от пути процесса, следовательно можно получать разные неизвестные значения энергий Гиббса образования из уравнений, в которых с одной стороны записаны суммы энергий продуктов реакции, а с другой - суммы энергий исходных веществ.

При пользовании значениями стандартной энергии Гиббса критерием принципиальной возможности процесса в нестандартных условиях принимается условие ΔG° < 0, а критерием принципиальной невозможности — условие ΔG° > 0. В то же время, если стандартная энергия Гиббса равна нулю, это не означает, что в реальных условиях (отличных от стандартных) система будет в равновесии.

Условия самопроизвольного протекания процессов в закрытых системах:

∆G<0, dG<0;

∆F<0,dF<0.

Константа равновесия

Количественной характеристикой химического равновесия является константа равновесия, которая может быть выражена через равновесные концентрации С, парциальные давления P или мольные доли X реагирующих веществ. Для некоторой реакции

соответствующие константы равновесия выражаются следующим образом:

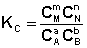
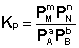
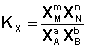
Константа равновесия есть характерная величина для каждой обратимой химической реакции; величина константы равновесия зависит только от природы реагирующих веществ и температуры. Выражение для константы равновесия для элементарной обратимой реакции может быть выведено из кинетических представлений.

Приняв, что V₁ = V₂, можно записать:

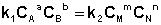
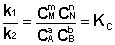
Таким образом, константа равновесия есть отношение констант скорости прямой и обратной реакции. Отсюда вытекает физический смысл константы равновесия: она показывает, во сколько раз скорость прямой реакции больше скорости обратной при данной температуре и концентрациях всех реагирующих веществ, равных 1 моль/л.