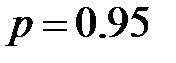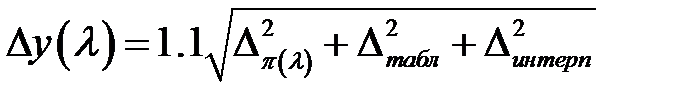Статистическая обработка группы результатов равноточных наблюдений

1. Исключение грубых ошибок

Внешним признаком результата, содержащего грубую ошибку, явля­ется его резкое отличие по величине от результатов остальных изме­рений. Статистический анализ наличия грубых ошибок заключается в определении вероятности того, что данное измерение содержит «промах» и сравнение ее с некоторым заранее заданным малым уровнем этой вероятности ( P=0.05 ; 0.01 либо 0.001). Часто применяется

сравнение «выскакивающего» значения с критерием Шовене, справедливого

для нормального закона распределения погрешностей измерений.

Для этого:

1.1. По результатам n измерений некоторой величины определяется среднеарифметическое значение

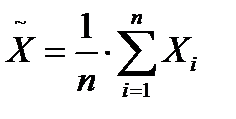
1.2. Вычисляется абсолютная кажущаяся погрешность

;

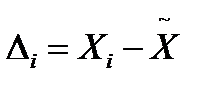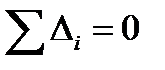
Погрешность называется кажущейся, поскольку она вычисляется относительно не истинного значения величины, а ее оценки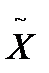

1.3. Определяется среднее квадратическое отклонение отдельного наблюдения (эмпирический стандарт)

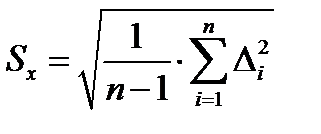
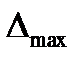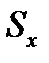1.4. Сравнивается погрешность "выскакивающего" наблюдения с и критерием Шовена

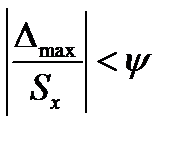
Величина критерия Шовене зависит от количества наблюдений n , ис­пользуемых при обработке.

Таблица 1. Значения критерия Шовене в зависимости от числа измерений

S	5	6	8	10	15	20	30	40	60	100
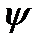	1.64	1.71	1.85	1.96	2.13	2.24	2.39	2.50	2.64	2.81

Если 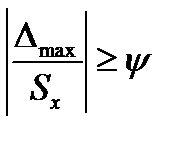, то результат наблюдения , выполненного с погрешностью 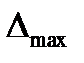считается грубой ошибкой и исключается из даль­нейший обработки.

2. Оценка результата измерения

;

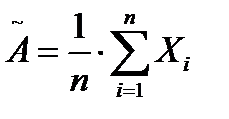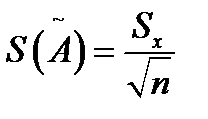
где 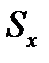, , 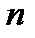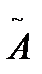определяются за вычетом грубых ошибок ("промахов").

Величина 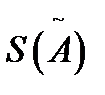измеряется в тех же единицах, что и резуль­таты наблюдений.

3. Определяются доверительные границы случайной погрешности.

Доверительные границы 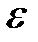случайной погрешности результата

измерения - это тот интервал, в который с заданной вероятностью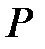

должно попасть среднее арифметическое значение при бесконечном увеличении объема выборки (увеличении количества наблюдений).

Величина 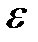без учета знака вычисляется по формуле

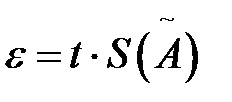
где t- коэффициент Стьюдента 9 квантиль Стьюдента ), зависящий от доверительной вероят­ности 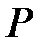и числа результатов наблюдений 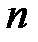(см.таблицу 2).

4. Определяют доверительные границы не исключённой систематической погрешности.

В экспериментальной практике встречаются случаи, когда невоз­можно заранее определить величину систематической погрешности и внести на нее поправку в результаты наблюдений.

Границы неисключенной систематической погрешности 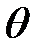резуль­тата измерений вычисляются как композиция всех неисключенных си­стематических погрешностей, вызванных всеми причинами, поддающи­мися учету:

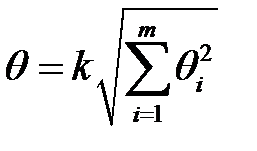, где 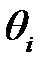- границы 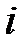-ой не исключенной систематической погрешности; т- количество учитываемых систематических погрешностей; 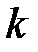- коэффициент, определяемый принятой доверительной вероят­ностью. Для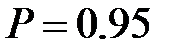

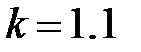
Для 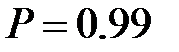значение коэффициента 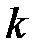зависит от числа 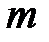и от соотношения величин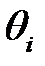

При ;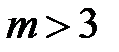

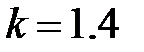
Пр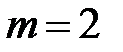и и ;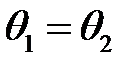

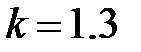
Если 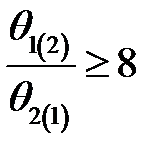, то 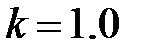Внутри указанного диапазона допустима интерполяция.

5. Определяются доверительные границы погрешности

результата измерения.

5.1. Если 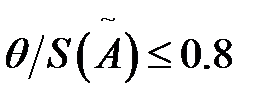, то не исключенную систематическую погреш­ность можно не учитывать, т.е. в этом случае суммарная пог­решность результата измерения определяется случайной погрешно­стью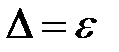

5.2. Если 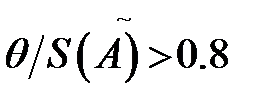, то суммарная погрешность результата из­мерения целиком определяется неисключенными систематическими погрешностями и случайные погрешности можно не учитывать .

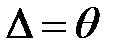Таблица 2 Значения 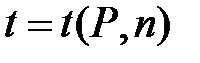коэффициента Стьюдента

P	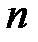0.95	0.99
∞	2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,201 2,179 2,160 2,145 2,131 2,120 2,103 2,086 2,060 2,042 2,030 2,021 2,014 2,008 2,000 1,995 1,990 1,987 1,984 1,960	4,604 4,032 3,707 3,499 3,355 3,250 3,169 3,106 3,055 3,012 2,977 2,947 2,921 2,878 2,845 2,787 2,750 2,724 2,704 2,689 2,677 2,660 2,648 2,639 2,632 2,626 2,576

Такое положение часто встречается при технических измерениях.

5.3. Если 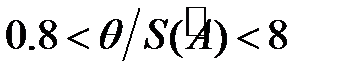то суммарную погрешность вычисляют как композицию случайной и не исключенных систематических погрешностей

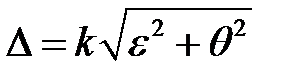
Выбор 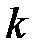см. пункт4, т.е.,

если 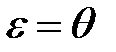,то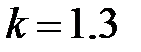

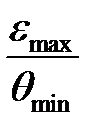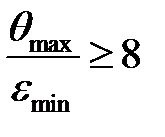если или , то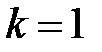

На этом обработка группы наблюдений заканчивается и результат прямого измерения записывается как: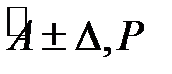

Если у экспериментатора возникают сомнения в том, что случайные отклонения результатов измерения подчиняются нормальному закону распределения, то необходимо выполнить специальное экспериментальное исследование для выяснения характера распределения , в котором число наблюдений должно быть сто и более.

Обработка результатов косвенных измерений

Результаты косвенных измерений обрабатываются с использова­нием результатов обработки прямых измерений:

1. Оценка измеряемой величины: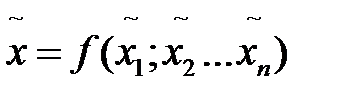

2. Весовые коэффициенты погрешностей прямых измерений:

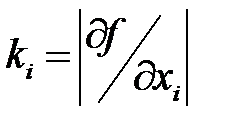
3. Погрешность результата:

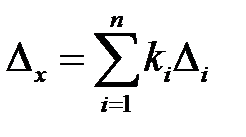
4. Среднее квадратическое отклонение погрешностей:

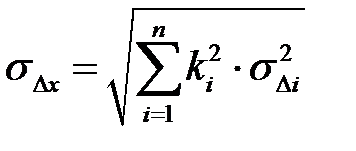
В данной лабораторной работе косвенными измерениями являются расходы воздуха 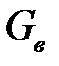и топлива 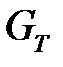. Для расчета расхода воздуха исполь­зуется известная из газовой динамики формула (*):

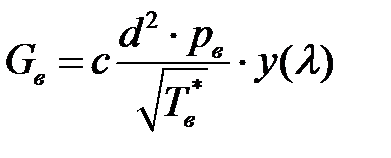
Таким образом, весовые коэффициенты для определения погрешности измерения расхода воздуха могут быть рассчитаны по формулам:

; ; ; ; .

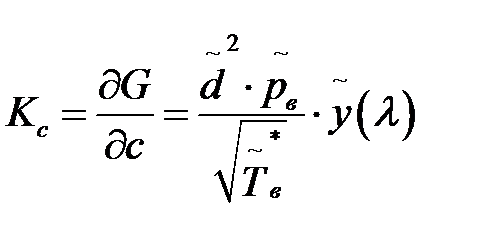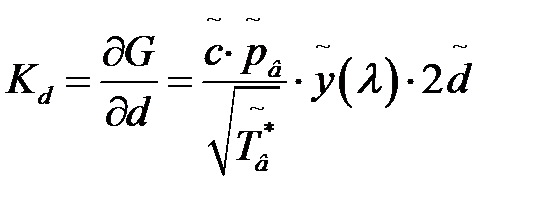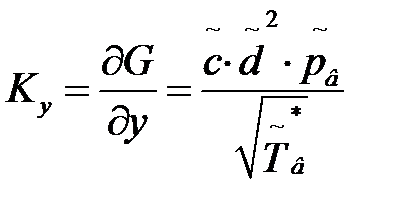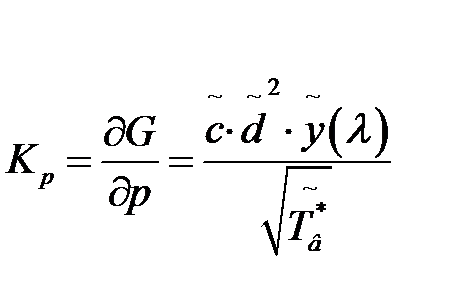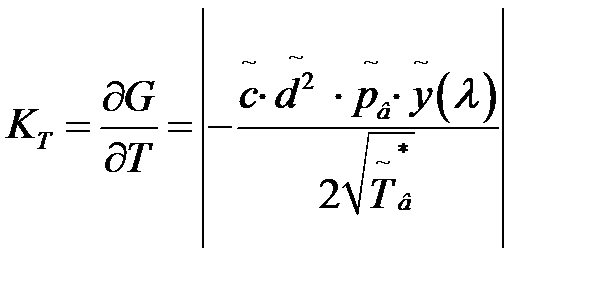Для вычисления абсолютной погрешности результата 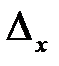необ­ходимы величины 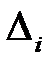. Ряд значений 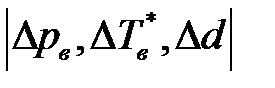получен при обработке прямых измерении . Величина 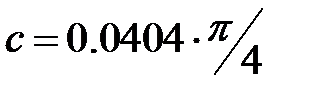- константа, точность определения которой зависит от количества знаков посла запятой в числе 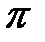.При обычной форме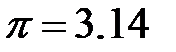

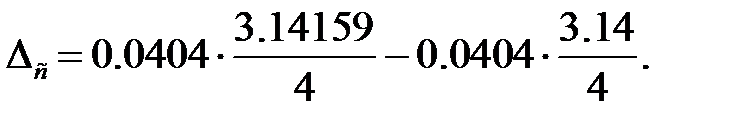
ГДФ 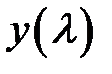находится из таблиц по аргументу 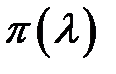, который в свою очередь является результатом косвенного измерения 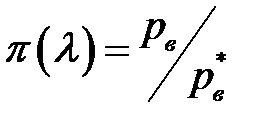. Все таблицы составлены с погрешностью округления чисел, равной по­ловине последнего разряда, т. 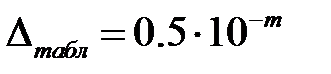е. ,где 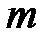- раз­ряд числа, до которого произведено округление. Следовательно, для используемых таблиц где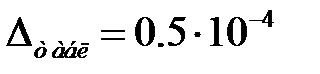

Когда находится функция 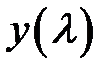при не табличных значениях аргумента 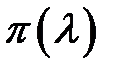, обычно производится линейная интерполяция, которая также имеет некоторую погрешность 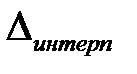. Большинство математических таблиц составлены так, что шаг таблицы и её точность - согла­сованы. При этом на любом участке таблицы ошибка линейной интерпо­ляции не превосходит единицы младшего разряда табличных значений функции. В противном случае обычно указывается порядок допустимой интерполяции. Следовательно, при интерполяции внутри интервалов таблиц ГДФ, в получаемый результат вносится погрешность .

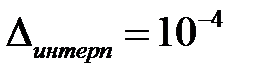Погрешность, вычисления 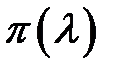рассчитывается как погрешность косвенного измерения

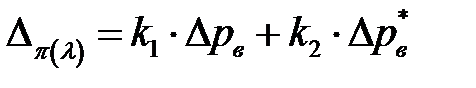
где

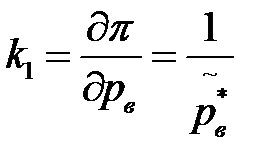и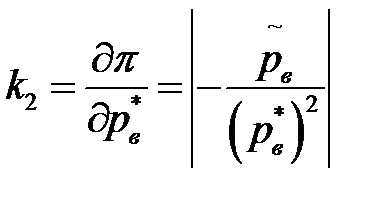

Таким образом, погрешность 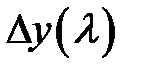является композицией перечисленных выше погрешностей, т.е. при доверительной вероятности