Кодирование целых и действительных чисел
ЛЕКЦИЯ №2-3.
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ, ТЕКСТОВОЙ И ГРАФИЧЕСКОЙ ИНФОРМАЦИИ В ЭВМ. СИСТЕМЫ СЧИСЛЕНИЯ.
ДАННЫЕ
Носители данных
Данные представляют собой зарегистрированные сигналы. В соответствии с методом регистрации данные могут храниться и транспортироваться на носителях различных видов.
Самым распространенным носителем данных является бумага. Изменение оптических свойств используется также в устройствах, осуществляющих запись лазерным лучом на пластмассовых носителях с отражающим покрытием (CD-ROM). В качестве носителей, использующих изменение магнитных свойств, можно назвать магнитные ленты и диски.
Регистрация данных путем изменения химического состава поверхностных веществ носителя широко используется в фотографии. На биохимическом уровне происходит накопление и передача данных в живой природе.
Любой носитель можно характеризовать параметром разрешающей способности (количеством данных, записанных в принятой для носителя единице измерения) и динамическим диапазоном (логарифмическим отношением интенсивности амплитуд максимального и минимального регистрируемого сигналов).
Операции с данными
Можно выделить следующие основные операции:
• сбор данных — накопление информации с целью обеспечения достаточной полноты для принятия решений;
• формализация данных — приведение данных, поступающих из разных источников, к одинаковой форме, чтобы повысить их уровень доступности;
• фильтрация данных — отсеивание «лишних» данных, в которых нет необходимости для принятия решений;
• сортировка данных — упорядочение данных по заданному признаку с целью удобства использования; повышает доступность информации;
• архивация данных — организация хранения данных в удобной и легкодоступной форме; служит для снижения экономических затрат по хранению данных и повышает общую надежность информационного процесса в целом;
• защита данных — комплекс мер, направленных на предотвращение утраты, воспроизведения и модификации данных;
• транспортировка данных — прием и передача (доставка и поставка) данных между удаленными участниками информационного процесса; при этом источник данных в информатике принято называть сервером, а потребителя — клиентом;
• преобразование данных — перевод данных из одной формы в другую или из одной структуры в другую.
Кодирование данных двоичным кодом
Естественные человеческие языки — это не что иное, как системы кодирования понятий для выражения мыслей посредством речи. Своя система существует и в вычислительной технике — она называется двоичным кодированием и основана на представлении данных последовательностью всего двух знаков: 0 и 1. Эти знаки называются двоичными цифрами, по-английски — binary digit или, сокращенно, bit (бит).
Одним битом могут быть выражены два понятия: 0 или 1. Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия:
00 01 10 11
Увеличивая на единицу количество разрядов в системе двоичного кодирования, мы увеличиваем в два раза количество значений, которое может быть выражено в данной системе, то есть общая формула имеет вид:
N=2m, где:
N — количество независимых кодируемых значений;
m — разрядность двоичного кодирования, принятая в данной системе.
Кодирование целых и действительных чисел
Для перевода чисел из десятичной системы счисления в систему с основанием p>1 обычно используют следующий алгоритм:
1. Если переводится целая часть числа, то она делится на р, после чего запоминается остаток от деления. Полученное частное вновь делится на р, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на Р выписываются в порядке, обратном их получению.
Целые числа кодируются двоичным кодом достаточно.
| 19 2 18 9 |
| 8 4 |
| 4 2 |
| 2 1 |
| 0 0 |
Таким образом, 1910= 100112 .
Для кодирования целых чисел от 0 до 255 достаточно иметь 8 разрядов двоичного кода (8 бит). Шестнадцать бит позволяют закодировать целые числа от 0 до 65535, а 24 бита — уже более 16,5 миллионов разных значений.
2. Если переводится дробная часть числа, то она умножается на р, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на р и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием р.
Пример. Перевести данное число из десятичной системы счисления в двоичную (получить пять знаков после запятой в двоичном представлении).
а) 380,1875(10); б) 115,94(10).
Решение. а) 380 0 1875 380,1875(10)=101111100,0011(2)
190 0 0 375
95 1 0 75
47 1 1 5
23 1 1 0
11 1
5 1
2 0
1 1
б) 115 1 94 115,94(10)=1110011,111100(2)
57 1 1 88
28 0 1 76
14 0 1 52
7 1 1 04
3 1 0 08
1 1 0 16
Для кодирования действительных чисел используют 80-разрядное кодирование. При этом число предварительно преобразуется в нормализованную форму:
3,1415926 = 0,31415926·101
300 000 = 0,3·106
123 456 789 = 0,123456789 · 1010
Первая часть числа называется мантиссой, а вторая — характеристикой. Большую часть из 80 бит отводят для хранения мантиссы (вместе со знаком) и некоторое фиксированное количество разрядов отводят для хранения характеристики (тоже со знаком).
Если необходимо перевести число из двоичной системы счисления в систему счисления, основанием которой является степень двойки, достаточно объединить цифры двоичного числа в группы по столько цифр, каков показатель степени, и использовать приведенный ниже алгоритм. Например, если перевод осуществляется в восьмеричную систему, то группы будут содержать три цифры (8=23). В целой части числа группировка производится справа налево, в дробной части — слева направо. Если в последней группе недостает цифр, дописываются нули: в целой части — слева, в дробной — справа. Затем каждая группа заменяется соответствующей цифрой новой системы. Соответствия приведены в таблице.
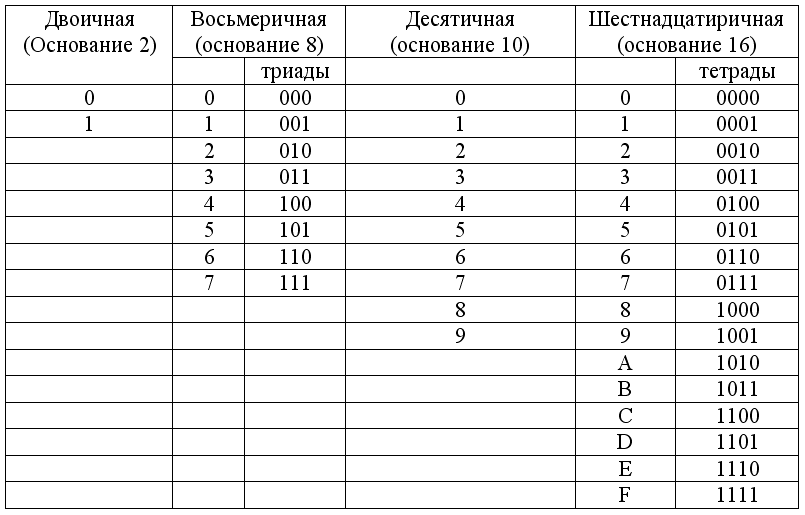
Переведем из двоичной системы в шестнадцатеричную число 1111010101,11(2). Решение 001111010101,1100(2)=3D5,C(16).
При переводе чисел из системы счисления с основанием р в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо (начальный номер — 1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда.
Это и есть представление исходного числа в десятичной системе счисления.
Пример. Перевести данное число в десятичную систему счисления:
а) 1000001(2)=1·26 + 0·25 + 0·24 + 0·23 + 0·22 + 0·21 + 0·25 + 1·20 =65(10).
Замечание. Если в каком-либо разряде стоит нуль, то соответствующее слагаемое можно опустить.
б) 1000011111,0101(2)=1·29 + 1·24 + 1·23 + 1·22 + 1·21 + 1·20 + 1·2-2 + 1·2-4 = 512+16+8+4+2+1+0,25+0,0625=543,3125(10).
в) 1216,04(8)=1·83 + 2·82 + 1·81 + 6·80 + 4·8-2 = 512+128+8+6+0,0625=654,0625(10).
г) 29А,5(16)=2·162 + 9·161 + 10·160 + 5·16-1 = 512+144+10+0,3125=656,3125(10).
Для выполнения арифметических операций в системе счисления с основанием р необходимо иметь соответствующие таблицы сложения и умножения.
| + | ||
| × | ||
| + | ||||||||
| × | ||||||||
| + | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
| × | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | C | E | 1A | 1C | 1E | |||||||||||
| С | F | 1B | 1E | 2A | 2D | |||||||||||
| C | 1C | 2C | 3C | |||||||||||||
| A | F | 1E | 2D | 3C | 4B | |||||||||||
| C | 1E | 2A | 3C | 4E | 5A | |||||||||||
| E | 1C | 2A | 3F | 4D | 5B | |||||||||||
| 1B | 2D | 3F | 5A | 6C | 7E | |||||||||||
| A | A | 1E | 3C | 5A | 6E | 8C | ||||||||||
| B | B | 2C | 4D | 6E | 8F | 9A | A5 | |||||||||
| C | C | 3C | 6C | 9C | A8 | B4 | ||||||||||
| D | D | 1A | 4E | 5B | 8F | 9C | A9 | B6 | C3 | |||||||
| E | E | 1C | 2A | 7E | 8C | 9A | A8 | B6 | C4 | D2 | ||||||
| F | F | 1E | 2D | 3C | 4B | 5A | A5 | B4 | C3 | D2 | E1 |
Пример. Сложить числа:
а) 10000000100(2)+ 111000010(2)= 10111000110(2);
+ 10000000100
111000010
10111000110(2).
б) 223,2(8)+ 427,54(8) = 652,74(8);
+ 223,2
427,54
652,74(8).
в) ЗВЗ,6(16)+38В,4(16)=73Е,A(16);
+ 3B3,6
38B,4
73E,A(16).
Пример. Выполнить вычитание:
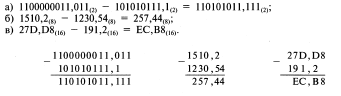
Пример:Выполнить умножение:

