Действие магнитного поля на проводник с током и заряд

В качестве силовой характеристики магнитного поля в данной точке удобно использовать вектор , модуль которого , а направление совпадает с положительным направлением нормали к контуру. Эта величина называется вектором магнитной индукци.

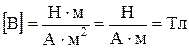(тесла)

Т.к. 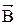характеризует силовое действие магнитного поля на ток, то индукция является аналогом напряженности электрического поля 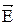. Распределение вектора магнитной индукции 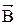в магнитном поле по аналогии с распределением 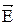в электрическом изображают с помощью силовых линий, касательные к которым в каждой точке поля совпадают с направлением 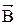. Силовые линии охватывают проводники с током и всегда замкнуты (рис.3 Тр,с177 прямой круговой). Их направление определяется правилом буравчика. Число линий на единицу площади поперечного сечения в данном месте соответствует модулю вектора .

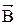ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ПРОВОДНИК С ТОКОМ И ЗАРЯД

Ампер установил, что на элементарный участок dl проводника с током I действует сила

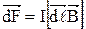, модуль которой dF = I∙B∙dl∙sinα, (1)

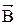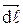где α – угол между и . Направление этой силы определяется правилом левой руки: линии индукции входят в ладонь, четыре вытянутые пальцы направлены по току, тогда отставленный большой палец укажет направление силы. Отсюда следует, что сила Ампера всегда перпендикулярна плоскости, в которой лежат 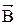и .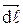

Т.к. ток, это направленное движение зарядов, то на каждую движущуюся заряженную частицу в магнитном поле будет действовать сила. Рассмотрим участок проводника длиной l, поперечным сечением S и концентрацией заряженных частиц n. Плотность тока в проводнике – j = nqυ (υ – скорость дрейфа зарядов под возлействием электрического поля), а сила тока – I = j·S = nqυ·S, . Теперь силу, действующую на движущуюся заряженную частицу в магнитном поле – силу Лоренца, можно выразить соотношением:

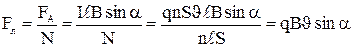, (2)

где N = n·Sl – общее число заряженных частиц на участке.

Направление силы Лоренца тоже определяется по правилу левой руки. Однако следует помнить, что для положительных зарядов четыре вытянутые пальца располагаются по вектору скорости, а для отрицательных – против.

Т.к. 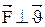, то это означает, что сила Лоренца не может изменить величину скорости, но изменяет направление вектора скорости в пространстве, т.е. сообщает заряду нормальное (центростремительное) ускорение. В результате этого в простейшем случае, когда 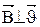, заряд q в магнитном поле будет двигаться по дуге окружности, радиусом R:

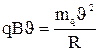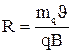→ (3)

и периодом обращения

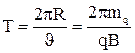. (4)

Эти простые соотношения лежат в основе объяснения принципов действия, таких известных приборов как ускорителей заряженных частиц и масс-спектрографа.

В общем случае, когда заряженные частицы влетают в магнитное поле под углом, то их движение можно представить как суперпозицию: равномерного прямолинейного со скоростью υ_ïç = υ·cosa вдоль силовых линий; и равномерного обращения со скоростью υ_^ = υ·sina вокруг силовых линий в плоскости перпендикулярной полю (рис. ). В результате образуется движение по спирали вдоль силовых линий. Винтовая линия (траектория) имеет радиусом R и шаг:

h = υ_ïç∙Т = υТ ·cosa = 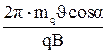. (5)

ЭФФЕКТ ХОЛЛА

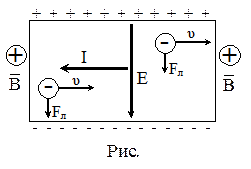Если поместить металлическую (или полупроводниковую), пластинку, по которой течет ток плотностью j, в магнитное поле с индукцией В,то в пластинке возникнет поперечное электрическое поле с напряженностью Е. Это явление получило название эффекта Холла.

На (рис.) представлены направления движения зарядов, силы тока, вектора индукции магнитного поля В и возникающей при этом силы Лоренца F_л. Действие силы Лоренца вызовет перемещение отрицательных зарядов к нижнему краю пластинки, соответственно положительных – к верхнему. В результате, возникает поперечное электрическое поле с напряженностью Е, которое будет препятствовать поперечному движению заряженных частиц. В некоторый момент кулоновская сила этого поля уравновесит силу Лоренца. При этом установится постоянное стационарное распределение зарядов в поперечном направлении. Определим поперечную (холловскую) разность потенциалов между краями пластинки. Из условия равновесия сил для металлов получим:

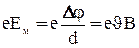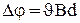, . (6)

Из соотношения для плотности тока: j = neυ, получим – υ = j / ne. Окончательно холловская разность потенциалов:

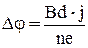. (7)

Датчики Холла широко используются: в измерительной технике; для определения природы носителей тока и их концентрации; при изучении энергетического спектра носителей; в аналоговых вычислительных машинах…

МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

Сходство в расположении силовых линий кругового тока и прямого магнита (рис.4 ТР с163) позволило Амперу в 1820 году выдвинуть гипотезу, что магнитные свойства вещества обусловлены наличием в них круговых микротоков, связанных с движением электронов вокруг ядра.

Если тело внести в магнитное поле проводника с током (макроток), то под его воздействием микротоки всех атомов сориентируются определенным образом, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции 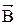характеризует результирующее поле, создаваемое всеми макро- и микротоками. Это означает, что при одном и том же макротоке и прочих равных условиях значение индукции В в разных средах будет разным.

Магнитное поле проводника с током (макротока) характеризуется вектором напряженности 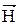. Для однородной изотропной среды

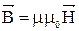, (8)

где μ – магнитная проницаемость среды, безразмерная величина, которая показывает, во сколько раз поле макротока усиливается или ослабляется за счет полей микротоков среды (для вакуума μ = 1); μ₀ = 4π∙10^-7 Гн/м.– магнитная постоянная. [Н] =А/м.

а) Магнитные моменты электрона, атома и молекулы

Рассмотрим явление намагничивания с точки зрения строения атомов и молекул. Будем считать, что электроны в атоме движутся по круговым орбитам (рис. ). Тогда каждый из электронов обращающийся по орбите с частотой ν (ν – число оборотов за секунду) создает микроток силой:

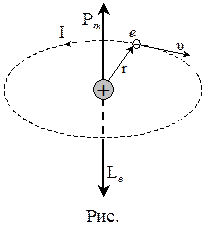I = еν, (9)

что обуславливает появление у электрона орбитального магнитного момента: 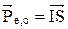. Модуль вектора:

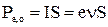, (10)

где S – площадь, охватываемая орбитой. С другой стороны модуль орбитального механического момента импульса электрона можно представить в виде:

L_e,о = m_eυ·r = m_e·2πrν ·r – 2m_eνS, (11)

где υ = 2πr∙ν, S = πr². Из рис. видно, что 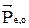и 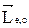по направлению противоположны. Тогда с учетом (10) и (11) для 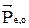получим:

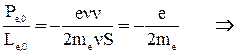
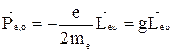. (12)

Величина g_ор = -е / 2m_е называется гиромагнитным отношением орбитальных моментов. Это соотношение справедливо и для эллиптических орбит.

Эксперимент показал, что измеренное гиромагнитное отношение для электрона вдвое больше g_ор. Было высказано предположение (впоследствии доказанное), что электрон кроме орбитального обладает собственным механическим моментом импульса 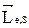, который называется спином. Спин – это свойство электрона, которому соответствует собственный (спиновый) магнитный момент. По аналогии с (12):

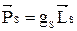, (13)

где g_S – спиновое гиромагнитное отношение.

Особенностью 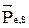является то, что его проекция на направление 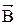принимает только одно из двух значений, т.к. 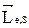квантуется:

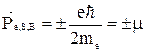_Б, (14)

где 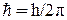, h – постоянная Планка. Величина μ_Б называется магнетоном Бора и является единицей магнитного момента электрона. Т.е. магнитный момент электрона может иметь значения только кратные μ_Б.

Т.к. магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, то ими можно пренебречь в данном случае. Тогда общий магнитный момент атома или молекулы будет представлять собой векторную сумму магнитных моментов (орбитальных и спиновых) входящих в атом или молекулу электронов:

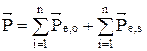, (15)

В общем случае магнитные моменты отдельных атомов и молекул ориентированы хаотически, поэтому тела в большинстве случаев не проявляют магнитных свойств. Однако все вещества являются магнетиками, т.е. способны под воздействием внешнего магнитного поля намагничиваться (приобретать магнитный момент, как результат упорядоченности в расположении магнитных моментов отдельных атомов и молекул).

Количественно намагничивание характеризуется вектором намагниченности – .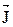

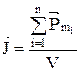, (16)

где 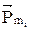– магнитный момент отдельной частицы, V– объём тела. [J] = А/м.

Как показывает опыт, намагниченность пропорциональна напряжённости внешнего поля:

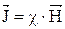, (17)

где χ – магнитная восприимчивость вещества (безразмерная величина, характеризующая способность вещества намагничиваться).

Вектор магнитной индукции магнитного поля в магнетике представляет собой сумму магнитной индукции 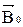внешнего поля (поле намагничивающего тока в вакууме) и поля микротоков 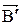(поля молекул и атомов магнетика):

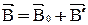. (18)

Известно, что 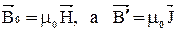. С учётом (4) выражение для 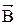теперь примет вид:

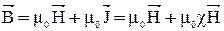. (19)

Из () получим для напряжённости внешнего поля:

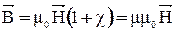, (20)

где 1+ χ = μ – магнитная проницаемость среды.

б) Диамагнетизм.

Для понимания механизма этого явления рассмотрим действие магнитного поля на движущийся в атоме электрон.

Орбиты электронов ориентированы относительно 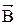произвольно. Пусть нормаль к плоскости орбиты – 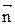образует с 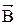угол α. В этом случае сила Лоренца, действуя, на движущийся электрон, вызывает прецессионное движение орбиты (опыт с волчком). Это вращательное движение орбиты эквивалентно круговому току, который в соответствии с правилом Ленца имеет такое направление, чтобы магнитное поле этого прецессионного тока было противоположно внешнему. Т.е. результирующее наведенное магнитное поле атомов ослабляет внешнее поле. Это явление получило название диамагнитного эффекта. Диамагнетизм, как явление, присущ всем материалам.

В зависимости от того будет ли индукция магнитного поля в данном веществе в результате намагничивания возрастать или убывать материалы делятся на диамагнетики и парамагнетики.

в) Диамагнетики

К диамагнетикам относятся вещества, у которых магнитные моменты молекул в отсутствие внешнего магнитного поля равны нулю. Внешнее магнитное поле вызывает диамагнитный эффект. Наведённые составляющие магнитных полей молекул складываются и образуют собственное магнитное поле вещества, которое направленно противоположно внешнему и ослабляет его. К диамагнетикам относятся: металлы – висмут, серебро, золото, медь и др.; большинство органических соединений; смолы; углерод; вода…

Г) Парамагнетизм

У молекул парамагнитных веществ орбитальные, спиновые и ядерные магнитные моменты не компенсируют друг друга. Поэтому атомы парамагнитных веществ обладают не равным нулю результирующим магнитным моментом Р_m. Моменты отдельных молекул расположены хаотично и в целом вещество не обнаруживает магнитных свойств. Внешнее поле стремиться сориентировать 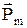по направлению поля. В результате парамагнетик намагничивается, т.е. в нём появляется собственное поле, совпадающее по направлению с внешним. Возникает парамагнитный эффект – внешнее поле усиливается. Интенсивность намагничивания (суммарный магнитный момент единицы объёма в данном случае будет зависеть не только от 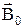внешнего поля, но и от температуры. При ликвидации внешнего поля тепловое движение разрушает ориентацию атомных магнитных моментов.

Удельная магнитная восприимчивость парамагнитных веществ

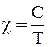– закон Кюри, (21)

где С – константа, характерная для каждого вещества. Т – температура.

В парамагнетике имеет место и диамагнитный эффект, однако он значительно слабее парамагнитного. Парамагнетиками являются: редкоземельные элементы, азот, кислород, алюминий и др. вещества, магнитная проницаемость которых μ > 1, а χ = 10^-15 ¸ 10^-3. В очень сильных магнитных полях наступает насыщение намагниченности. Это означает, что все Р_m атомов (молекул) ориентированы вдоль внешнего поля. Для диа- и парамагнетиков намагниченность 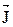изменяется в зависимости от 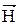по линейному закону.

Д) Ферромагнетики

Помимо слабомагнитных веществ, к которым относится диамагнетики и парамагнетики, существует еще сильномагнитные вещества ферромагнетики. Намагниченность ферромагнетиков имеет тенденцию к насыщению. Существенной особенностью этого класса веществ являются: а) большие значения магнитной проницаемости 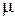(для Fe – 5000, супермаллоя – 800000) и б) зависимость μ от H (рис.). Такой характер поведения μ обуславливает явление магнитного гистерезиса – зависимость 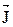не только от H, но и от того какой была намагниченность в предыдущий момент.

Формула 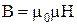справедлива и для ферромагнетиков, однако магнитная индукция теперь не будет пропорциональна напряжённости намагничивающего поля, т.к. μ = f(H). Уже при сравнительно небольшой напряжённости H индукция B достигает большого значения после чего она изменяется медленно пропорционально H, рис.18.см рукопись

Если в ферромагнетике, намагниченном до насыщения B_н начать уменьшать напряжённость поля H, то индукция B тоже будет уменьшаться: однако её уменьшение происходит не по линии (1 – 0), а по (1 – 2), рис.19. При H = 0 ферромагнетик не размагничивается полностью. Отрезок (0 – 2) выражает остаточную магнитную индукцию – B₀. Для полного размагничивания необходимо создать внешнее поле с напряжённостью H_к противоположного направления. Эта напряжённость называется коэрцетивной силой. Дальнейший рост напряжённости поля вызывает перемагничивание ферромагнетика – (3 – 4) и при H = -H_н намагнитится до насыщения но в противоположном к исходному направлении. Затем его можно снова размагнитить (4 – 5 – 6) и снова намагнитить (6 – 1).

Явление отставания изменений магнитной индукции от изменений напряжённости намагничивающего поля называется магнитным гистерезисом. Кривая 1-3-4-6-1 – петлёй гистерезиса.

Площадь петли характеризует работу, затрачиваемую внешним полем на однократное перемагничивание ферромагнетика. Эта работа выделяется в виде теплоты.

При нагревании до определённой температуры (точка Кюри) ферромагнетики теряют свои магнитные свойства и превращаются в парамагнетик с μ ≈ 1. Точка Кюри для Fe - 770˚C, для Ni - 360˚C).

Особенности ферромагнетика обусловлены тем, что в нём имеется множество сравнительно крупных самопроизвольно намагниченных до насыщения областей – доменов, размером порядка 10^-2 см. В пределах одного домена спиновые магнитные моменты электронов ориентированы одинаково, что доказано на опытах Эйнштейном, Де-Гаазом и Иоффе. Однако ориентация самих доменов хаотична. Поэтому в отсутствие магнитного поля ферромагнетик не обнаруживает намагниченности. Внешнее поле упорядочивает ориентацию доменов. При напряжённости поля H_μ все домены занимают положение, при котором их магнитные моменты ориентированы в направлении внешнего поля – ферромагнетик намагничивается до насыщения. При выключении поля ферромагнетик не размагничиватся полностью. Этим объясняется магнитный гистерезис.

Ферромагнитики с широкой петлей гистерезиса называются жесткими, а с узкой мягкими.