Погрешности анализа

Абсолютные и относительные погрешности. Выше уже упоминалась важная метрологическая характеристика любого измерительного процесса – погрешность. Дадим ей теперь более строгое определение.

Погрешность – это разность между результатом измерения и действительным значением измеряемой величины.

Соответственно, погрешность количественного анализа – это разность между результатом анализа (будем далее его обозначать символом х) и действительным значением измеряемой величины (m). Значение m можно узнать, если измерить ту же величину по некоторой стандартной методике, заведомо дающей пренебрежимо малую погрешность.

Погрешности могут быть выражены в абсолютной или относительной форме. Абсолютную погрешность (D) находят по формуле

D = х – m.

Величина D всегда выражается в тех же единицах, что и сама измеряемая величина, причем D имеет определенный знак. Результат измерения (или анализа) называют завышенным, если D > 0 (т. е. х > m), и заниженным, если D < 0 (т. е. х < m).

Измерения лучше характеризовать не абсолютной, а относительной погрешностью. Чтобы найти относительную погрешность (d) результата анализа, надо разделить абсолютную погрешность на истинное содержание компонента в исследуемом материале,

d = D / m.

Так как х » m, можно охарактеризовать величину d и отношением D / х. Относительная погрешность – безразмерная величина, но ее можно выразить в процентах, если умножить d на 100. Ни относительную, ни абсолютную погрешности нельзя точно измерить, если неизвестно действительное содержание компонента в данном объекте, а такая ситуация является типичной. Но приблизительно оценить погрешность анализа можно и в этом случае (см. 2.6).

В контроле производства, в клиническом анализе и во многих других случаях используют только такие методики анализа, для которых величина погрешности не превышает некоторый заранее заданный предел.

Погрешности можно классифицировать по месту и времени возникновения. Почти в любом химическом анализе можно выделить погрешность пробоотбора, иногда она является главной составляющей общей погрешности анализа. Есть и другие составляющие: так, инструментальные погрешности обусловлены неточностью используемых приборов и мерной посуды, примесями в реактивах и другими факторами, связанными со средствами измерений. Методические погрешности связаны с неверно выбранной методикой анализа, неточным выполнением операций, неконтролируемым влиянием изменяющихся условий и другими факторами. Существуют и субъективные погрешности, связанные с особенностями органов чувств или психики исполнителя анализа.

Случайные и систематические погрешности. В общей погрешности любого измерения, в том числе и в погрешности химического анализа, – обычно можно выявить два независимых слагаемых, две составляющих – случайную (y) и систематическую (q):

D = y + q .

Случайные и систематические погрешности возникают по разным причинам, их по-разному оценивают и по-разному устраняют. Хотя результат любого измерения всегда содержит обе составляющих, зачастую одна из них намного больше другой, которую называют незначимой и не учитывают при расчете общей погрешности. В таких случаях считают, что результат анализа содержит погрешность только одного типа.

Случайной погрешностью называют погрешность измерений (анализов), которая при повторных измерениях случайным образом меняется по величине и знаку.

Случайные погрешности возникают вследствие суммарного влияния целого ряда неконтролируемых факторов. Эти факторы обычно действуют непостоянно и разнонаправленно (одни ведут к завышенным, другие – к заниженным результатам измерений). Поэтому при повторных измерениях одной и той же величины по одной и той же методике получают разные результаты: то завышенные, то заниженные. Следовательно, от измерения к измерению меняются и величина, и знак случайной погрешности (y). Это изменение непредсказуемо, случайно; нельзя предугадать, какая именно величина y получится в данном измерении.

Как же в таком случае охарактеризовать случайные погрешности какого-либо измерительного процесса?Мера случайных погрешностей – стандартное отклонение. Оно характеризует близость результатов повторных измерений друг к другу, их разброс вокруг среднего арифметического. Результаты повторных измерений (анализов) называют вариантами, а совокупность нескольких однотипных вариант, полученных при повторных измерениях одной и той же величины, – выборкой. Термин «выборка» используется, поскольку аналитики рассматривают полученные варианты как случайно выбранные из генеральной совокупности всех результатов анализа данного материала, которые можно было бы получить по данной методике. Выборку характеризует величина выборочного стандартного отклонения (s):

s = 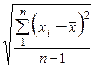, (2.3)

где х_i – результат i-го измерения (анализа); 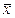– среднее арифметическое из результатов n повторных измерений; n – объем выборки (число вариант). Чтобы рассчитать стандартное отклонение, надо найти отклонение каждой варианты от среднего арифметического, рассчитать квадраты этих отклонений, просуммировать все квадраты, разделить полученную cумму на (n – 1) и извлечь квадратный корень. Значение s всегда положительно. Формулу (2.3) применяют для небольших выборок, обычно при n < 30. Стандартное отклонение можно рассчитать и для больших (n > 30) совокупностей экспериментальных данных, в этом случае его обозначают символом s и рассчитывают по формуле (2.4). Величиной s обычно характеризуют методику анализа в целом, это предел, к которому стремится s по мере увеличения объема выборки, т. е. при увеличении числа повторных анализов.

s = . (2.4)

Чем больше s (или s), тем, при прочих равных условиях, менее точен результат анализа, выраженный в виде среднего арифметического. Однако отсутствие случайных погрешностей (s = 0) вовсе не означает, что результат анализа правилен. Результаты повторных анализов могут совпадать и вследствие повторения одной и той же ошибки!

Систематической погрешностью называют погрешность измерения (анализа), которая при повторных измерениях остается постоянной по величине и знаку (или закономерно меняется по величине). Ее характеризуют разностью среднего результата анализа и действительного содержания компонента:

q = 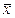– m.

Систематические погрешности возникают под действием постоянно действующих факторов. Величина q при повторных измерениях всегда остается постоянной по знаку. Обычно она остается постоянной и по величине. В отличие от случайной погрешности, систематическую можно предсказать заранее, если знать источник этой погрешности.

Оценить систематическую погрешность непросто – величина m, как правило, неизвестна, а величину 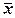в ходе оценки q необходимо находить по как можно большему числу повторных (или параллельно выполняемых) измерений (анализов). Для проверки правильности результата анализа и оценки q существует ряд приемов, они будут рассмотрены в разделе 2.4.

Правильность и воспроизводимость. Результат количественного анализа называют правильным, если средний результат ( 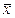) примерно совпадает с действительным содержанием определяемого компонента. Правильность результата определяется наличием или отсутствием значимой систематической погрешности. Другая характеристика – прецизионность анализа, котораяопределяется наличием или отсутствием значимой случайной погрешности. Частными случаями прецизионности являются воспроизводимость и сходимость. Термин «воспроизводимость» рекомендуется использовать, когда говорят о серии результатов анализа одного материала, полученных по разным методикам, разными исполнителями, на разных приборах, в разных лабораториях. Если же речь идет о повторных измерениях, выполненных в одних и тех же условиях, на одном приборе, одним исполнителем, – пользуются терминами «сходимость» или «повторяемость». Вместо рекомендуемого метрологами термина «прецизионность» химики часто используют термин «воспроизводимость» как обобщающее понятие. Тогда в качестве частных случаев рассматривают сходимость и собственно воспроизводимость (например, межлабораторную). Далее используется именно эта терминология, хотя она не вполне строгая.

Точность – обобщенная качественная характеристика результатов количественного анализа, отражающая их близость к действительному содержанию определяемого компонента. Средний результат анализа считают точным, если он одновременно и правилен, и хорошо воспроизводим. В этом случае обе составляющих общей погрешности – и случайная, и систематическая – одновременно близки к нулю.

Рассматривая результаты анализа конкретного объекта, можно считать их достаточно точными, если погрешности анализа (случайная, систематическая и общая) не превышают заранее установленных пределов, допустимых для данного объекта и данной методики анализа. При этом учитывается не только абсолютное значение погрешности, но и ее относительная величина.

Пример 2.1. Некоторый материал независимо друг от друга исследовали четыре аналитика, каждый из них провел по 5 анализов. Действительное содержание (m) определяемого компонента в данном материале известно и составляет 30 единиц.

· Первый аналитик получил результаты: 68, 48, 36, 54 и 77 единиц. Среднее арифметическое 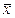= 56,6, q = 26,6. Формула (2.3) приводит к s = 16,2. Случайная и систематическая погрешности близки по величине, обе они весьма велики (того же порядка, что и средний результат анализа (q ≈ s ≈ 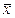). Очевидно, нельзя пренебречь ни той, ни другой составляющей общей погрешности. Надо сделать вывод, что полученные первым аналитиком результаты и неправильны, и плохо воспроизводимы.

· Результаты второго аналитика: 20, 32, 28, 40, 31 единиц. Величина 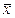равна 30,2, q = 0,2, s= 7,2. Полученные данные характеризуются довольно большой случайной погрешностью, по сравнению с ней систематической погрешностью можно пренебречь (s >> q). У второго аналитика средний результат анализа почти правилен, но плохо воспроизводим.

· Результаты третьего аналитика: 44, 43, 44, 44, 45 единиц, 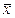= 44, q = 14, s = 0,7. Случайной погрешностью можно пренебречь, поскольку s намного меньше[1], чем q. Результаты имеют хорошую сходимость, но все они, как и их среднее арифметическое, сильно завышены, т. е. неправильны.

· Результаты четвертого аналитика: 31, 30, 31, 29 и 30 единиц, 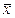= 30,2, q = 0,2, s = 0,8. Обе составляющие общей погрешности малы по сравнению со средним результатом. Результаты можно считать правильными и хорошо воспроизводимыми, а значит, точными.