Указание: во всех задачах считать газы идеальными
ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
Химическая термодинамика является наукой об энергетических эффектах химических реакций, их направлении и равновесии. Изучает применение законов термодинамики к химическим и физико-химическим процессам.
Термодинамический метод полезен тем, что позволяет:
- установить взаимосвязь между параметрами равновесной системы, что дает возможность вычислить неизвестный параметр системы по другим известным параметрам;
- оценить величину изменения параметров системы при осуществлении какого-либо процесса в ней;
- определить параметры системы после перехода ее из одного состояния в другое термодинамическое состояние или из одного технологического режима в другой режим проведения процесса;
- определить принципиальную возможность протекания процесса в нужном направлении;
- оценить глубину протекания процесса в зависимости от условий.
При определении параметров простейших термодинамических процессов идеальных газов используйте формулы, приведенные в таблицах 1.1 и 1.2. Необходимо обратить особое внимание на правильное применение соответствующих размерностей параметров. Используйте следующие значения универсальной газовой постоянной: R = 8,31 Дж/(моль·К) = 1,98 кал/(моль·К) = 0,082(л·атм)/(моль·К).
Тепловой эффект реакций при стандартных условиях определяется по формуле:

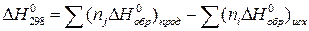 (1.1)
(1.1)
Соответствующие значения 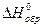 компонентов приведены в таблице 1.4.
компонентов приведены в таблице 1.4.
При расчете тепловых эффектов при других температурах необходимо опираться на закон Кирхгофа и на вытекающее из него уравнение:
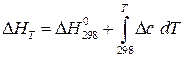 (интегральная форма), (1.2)
(интегральная форма), (1.2)
в котором Δс - разность суммы теплоемкостей продуктов и исходных реагентов:
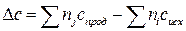 , (1.3)
, (1.3)
где индекс i – стехиометрические коэффициенты соответствующих исходных реагентов; j – стехиометрические коэффициенты соответствующих продуктов реакции.
При этом можно сделать следующие допущения:
1. Δс = 0. Тогда ΔHT = ΔH0298.
2. Δc = const. Тогда Δc определяется по значениям теплоемкости компонентов реакционной системы при стандартных условиях (таблица 1.4) и значение ΔHT вычисляют по формуле:
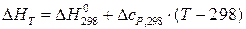 . (1.4)
. (1.4)
3. 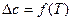 . При этом допущении необходимо учитывать температурную зависимость теплоемкости компонентов реакционной системы
. При этом допущении необходимо учитывать температурную зависимость теплоемкости компонентов реакционной системы
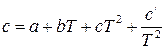 , (1.5)
, (1.5)
из которой следует
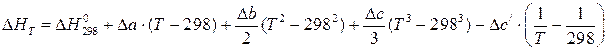 , (1.6)
, (1.6)
где 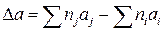 . Параметры
. Параметры 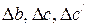 рассчитываются аналогичным образом. Значения а,b, c, c/ компонентов реакции приведены в таблице 1.4.
рассчитываются аналогичным образом. Значения а,b, c, c/ компонентов реакции приведены в таблице 1.4.
Изменение энтропии реакции при стандартных условиях определяются исходя из значений S0 (таблица 1.4) по формуле:
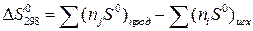 . (1.7)
. (1.7)
При определении 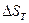 необходимо учитывать температурную зависимость теплоемкости компонентов от температуры:
необходимо учитывать температурную зависимость теплоемкости компонентов от температуры:
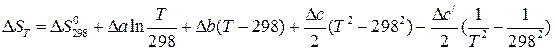 . (1.8)
. (1.8)
Вычисление 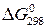 проводят по формуле:
проводят по формуле:
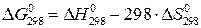 . (1.9)
. (1.9)
Значение 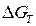 определяют по аналогичной формуле
определяют по аналогичной формуле
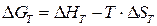 . (1.10)
. (1.10)
По знаку величин 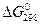 и
и 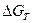 определяют возможное направление протекания реакции при стандартных условиях и при температуре Т.
определяют возможное направление протекания реакции при стандартных условиях и при температуре Т.
Если: DG < 0 – самопроизвольное протекание химической реакции возможно;
DG > 0 – самопроизвольное протекание химической реакции невозможно;
DG = 0 – система находится в равновесии.
Таблица 1.1 Связь между основными параметрами состояния в изопроцессах и определение их функции перехода для n молей вещества ( 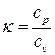 )
)
| Процесс | Уравнение процесса | Связь между параметрами состояния | Работа в процессе | Количество теплоты, сообщенное в процессе |
| Изобарный | 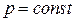 | 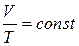 | 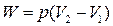 | 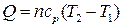 |
| Изотерми- ческий | 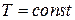 | 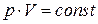 | 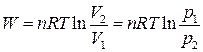 | 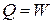 |
| Изохорный | 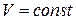 | 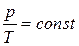 | 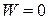 | 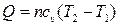 |
| Адиабатный | 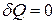 | 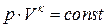 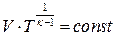 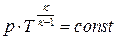 | 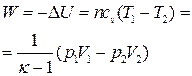 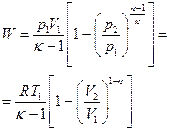 | 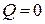 |
Таблица 1.2 Изменение функций состояния системы в изопроцессах (n - количество вещества, 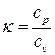 )
)
| Процесс | Изменение энтальпии | Изменение внутренней энергии | Изменение энтропии | Молярная теплоемкость |
| Изобарный | ΔН=ΔU+W=Q | ΔU=ncv(T2 – T1) | 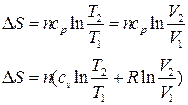 | 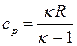 |
| Изотерми-ческий | ΔН = 0 | ΔU = 0 | 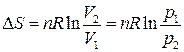 | 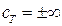 |
| Изохорный | ΔН= nсp(T2 –T1) | ΔU= ncv(T2 – T1) | 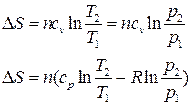 | 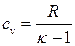 |
| Адиабатный | 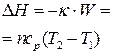 | 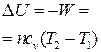 | 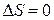 | сад = 0 |
Литература:[1], с. 12 – 69; [2], с. 8 – 49.
Примеры решения задач
Пример 1.1Рассчитайте изменение внутренней энергии гелия (одноатомный идеальный газ) при изобарном расширении от 5 до 10 л под давлением 196 кПа.
Решение: Из таблицы 1.2 для изобарного процесса находим ΔU = ncv(T2 – T1). Изменение внутренней энергии идеального газа определяется только начальной и конечной температурой: T1 = p1V1 /nR, T2 = p2V2 /nR. Для одноатомного идеального газа Cv = 3/2·nR.
DU = ncv (T2 – T1) = 3/2nR (T2 – T1) = 3/2(p2V2 – p1V1)= 3/2(196×103)×(10 - 5)×10-3 = =1470 Дж.
Ответ: DU = 1470 Дж.
Пример 1.2 Рассчитайте энтальпию сгорания метана при 1000 К, если даны энтальпии образования при 298 К: Df H° (CH4) = -17,9 ккал/моль, Df H° (CO2) = -94,1 ккал/моль, Df H° (H2O(г)) = -57,8 ккал/моль. Теплоемкости газов (в кал·моль-1·К-1) в интервале от 298 до 1000К равны:
сp(CH4) = 3,422 + 0,0178 × T; сp(O2) = 6,095+ 0,0033 × T;
сp(CO2) = 6,396 + 0,0102 × T; сp (H2O(г)) = 7,188 + 0,0024 × T.
Решение: Запишем уравнение процесса:
CH4(г) + 2O2(г) ® CO2(г) + 2H2O(г)
Энтальпия реакции при температуре Т рассчитывается по закону Кирхгоффа 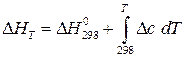 .
.
Чтобы им воспользоваться, необходимо рассчитать стандартную энтальпию реакции DH0298 и Dc – разность суммы теплоемкостей продуктов и исходных реагентов
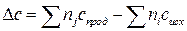 .
.
Стандартный тепловой эффект реакции определяется по формуле
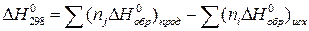 .
.
Для данной химической реакции:
DH°298 = Df H° (CO2) + 2∙Df H° (H2O(г)) – Df H° (CH4) = -94,1+ 2×(-57,8) – (-17,9) = = -191,8 ккал·моль-1.
Dсp = сp(CO2) + 2∙сp(H2O(г)) – сp(CH4) – 2∙сp(O2) = 6,396 + 0,0102×Т + 2×(7,188 + +0,0024×Т) – 3,422 – 0,0178×Т – 2×(6,095 + 0,0033×Т) = 5,16 – 0,0094×Т (кал·моль-1·К-1).
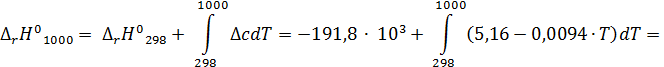
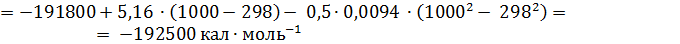
Ответ:DН1000= -192,5 ккал·моль-1.
Контрольные задания
1 Термодинамические системы и внешняя среда. Термодинамические параметры состояния системы.
2 Термодинамические процессы. Равновесные (квазистатические) и неравновесные процессы.
3 Понятие о внутренней энергии, теплоте и работе. Первое начало термодинамики, его математическое выражение.
4 Первое начало термодинамики для изохорного и изобарного процессов. Понятие об энтальпии.
5 Термохимия. Закон Гесса и следствия из него.
6 Тепловой эффект химической реакции, теплота образования химического вещества, теплота сгорания химического вещества.
7 Зависимость теплового эффекта реакции от температуры. Уравнение Кирхгофа.
8 Теплоемкость. Зависимость теплоемкости от температуры и расчет тепловых эффектов реакций.
9 Энергия химических связей. Оценки теплот химических реакций по энергиям связей.
10 Второе начало термодинамики. Энтропия и термодинамическая вероятность.
11 Расчет изменения энтропии для различных процессов.
12 Третье начало термодинамики. Расчет абсолютного значения энтропии.
13 Термодинамические потенциалы. Использование свободной энергии Гиббса и свободной энергии Гельмгольца для оценки возможности самопроизвольного протекания процессов.
14 Химические потенциалы, их определение, вычисление и свойства.
15 Газ, расширяясь от 10 л до 16 л при постоянном давлении 101,3 кПа, поглощает 126 Дж теплоты. Определите изменение внутренней энергии газа.
16 Определите изменение внутренней энергии, количество теплоты и работу, совершаемую при обратимом изотермическом расширении азота от 0,5 до 4 м3 (начальные условия: температура 26,8 °С, давление 93,2 кПа).
17 Один моль идеального газа, взятого при 25 °С и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощенную теплоту, изменение внутренней энергии и энтальпии.
18 Какое количество теплоты необходимо для повышения температуры 16 г кислорода от 300 до 500 К при давлении 1 атм? Как при этом изменится внутренняя энергия?
19 Чайник, содержащий 1 кг кипящей воды, нагревают до полного испарения при нормальном давлении. Определите работу, количество теплоты, изменение внутренней энергии и энтальпии для этого процесса. Мольная теплота испарения воды 40,6 кДж/моль.
20 Определите конечную температуру и работу, необходимую для адиабатического сжатия азота от 10л до 1 л, если начальные температура и давление равны 26,8°С и 101,3 кПа соответственно.
21 Рассчитайте количество теплоты, необходимое для нагревания воздуха в квартире общим объемом 600 м3 от 20 до 25 °С. Примите, что воздух – идеальный двухатомный газ, а давление при исходной температуре нормальное. Найдите изменение внутренней энергии и энтальпии для процесса нагревания воздуха.
22 Вычислите стандартную энтальпию реакции S(т) + O2(г) → SO2(г) , используя данные: 2S(т) + 3O2(г) → 2SO3(г), Dr H° = - 790 кДж,
2SO2(г) + O2(г) → SO3(г), Dr H° = - 196 кДж.
23 Вычислите тепловой эффект перехода C(алмаз) → C(графит), используя данные:
C(графит) + O2(г) → CO2(г), Dr H° = - 396,3 кДж,
C(алмаз) + O2(г) → CO2(г), Dr H° = - 398,2 кДж.
24 Вычислите тепловой эффект перехода S(моноклинная) → S(ромбическая), используя данные:
S(моноклинная) + O2(г) → SO2(г), Dr H° = - 296,96 кДж,
S(ромбическая) + O2(г) → SO2(г), Dr H° = - 396,65 кДж.
25 Определите стандартную энтальпию образования этилена C2H4 по следующим данным:
C2H4(г) +3O2(г) → 2CO2(г) + 2H2O(г), Dr H° = - 1323 кДж
C(графит) + O2(г) → CO2(г), Dr H° = - 393,5 кДж,
H2(г) + 1/2O2(г) → H2O(г), Dr H° = - 241,8 кДж.
26 Вычислите тепловой эффект реакции CH3OCH3(г) → CH3CH2OH(г), если
CH3OCH3(г) + 3O2(г) → 2CO2(г) + 3H2O(г), Dr H° = - 1454 кДж,
CH3CH2OH(г) + 3O2(г) → 2CO2(г) + 3H2O(г), Dr H° = - 1402 кДж.
27 Вычислите тепловой эффект реакции Na2CO3(т) → Na2O(т) + CO2(г), если известно
Na2CO3(т) + SiO2(т) → Na2SiO3(т) + CO2(г), Dr H° = 81,04 кДж,
Na2O(т) + SiO2(т) → Na2SiO3(т), Dr H° = - 243,17 кДж.
28 Рассчитайте мольную энтропию неона при 500 К, если при 298 К и том же объеме энтропия неона равна 146,2 Дж/моль×К.
29 Рассчитайте изменение энтропии при нагревании 11,2 л азота от 0 °С до 50 °С и одновременном уменьшении давления от 1 атм до 0,01 атм.
30 Один моль гелия при 100° С и 1 атм смешивают с 0,5 моль неона при 0 °С и 1 атм. Определите изменение энтропии, если конечное давление равно 1 атм.
31 Три моля идеального одноатомного газа (сv = 3 кал/моль×К), находящегося при 350 К и давлении 5 атм, обратимо и адиабатически расширяются до давления 1 атм. Рассчитайте конечные температуру, объем, совершенную работу, изменение внутренней энергии, энтальпии и энтропии в этом процессе.
32 Рассчитайте изменение энтропии при нагревании 0,4 моль NaCl от 20° до 850 °С. Мольная теплоемкость равна: сp(NaCl(тв)) = 45,94 + 16,32×10-3×T (Дж/моль×К),
сp(NaCl(ж)) = 66,53 Дж/моль×К. Температура плавления хлорида натрия 800 °С, теплота плавления 31 кДж/моль.
33 Рассчитайте изменение энтропии при смешении 5 кг воды при 80 °С с 10 кг воды при 20 °С. Удельную теплоемкость воды принять равной 4,184 Дж/г×К.
34 Рассчитайте изменение энтропии при добавлении 200 г льда, находящегося при температуре 0 °С, к 200 г воды (90 °С) в изолированном сосуде. Теплота плавления льда равна 6 кДж/моль. Удельную теплоемкость воды принять равной 4,184 Дж/г×К.
35 – 80 Многовариантная задача. Для реакции, приведенной в таблице 1.3:
1 рассчитайте стандартный тепловой эффект реакции по известным величинам стандартных теплот образования исходных веществ и продуктов реакции;
2 определите DНТ из предположения:
а) Dс = 0;
б) Dс = const;
в) Dс = f (Т).
3 определите 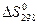 и DSТ для реакции;
и DSТ для реакции;
4 вычислите значение 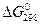 и DGТ и сделайте вывод о направлении реакции в стандартных условиях и при температуре Т.
и DGТ и сделайте вывод о направлении реакции в стандартных условиях и при температуре Т.
Термодинамические характеристики веществ приведены в таблице 1.4
Таблица 1.3 Уравнения реакций для различных вариантов
| № п/п | Реакция | Т, К |
| 2H2(г) + CO(г) = CH3OH(г) | ||
| 4HCl(г) + O2(г) = 2H2O(г) + 2Cl2(г) | ||
| NH4Cl(т) = NH3(г) + HCl(г) | ||
| 2N2(г) + 6H2O(г) = 4NH3(г) + 3O2(г) | ||
| 4NO(г) + 6H2O(г) = 4NH3(г) + 5O2(г) | ||
| 2NO2(г) = 2NO(г) + O2(г) | ||
| N2O4(г) = 2NO2(г) | ||
| Mg(OH)2(т) = MgO(т) + H2O(г) | ||
| CaCO3(т) = CaO(т) + CO2(г) | ||
| Ca(OH)2(т) = CaO(т) + H2O(г) | ||
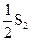 (г) + 2Н2О(г) = SO2(г) + 2H2(г) (г) + 2Н2О(г) = SO2(г) + 2H2(г) | ||
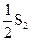 (г) + 2СО2(г) = SO2(г) + 2CO(г) (г) + 2СО2(г) = SO2(г) + 2CO(г) | ||
| 2SO2(г) + O2(г) = 2SO3(г) | ||
| SO2(г) + Cl2(г) = SO2Cl2(г) | ||
| CO(г) + 3H2(г) = CH4(г) + H2O(г) | ||
2CO(г) + SO2(г) = 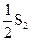 (г) + 2СО2(г) (г) + 2СО2(г) | ||
| CO(г) + Cl2(г) = COCl2(г) | ||
| CO2(г) + H2(г) = CO(г) + H2O(г) | ||
| CH4 + CO2 = 2CO + 2H2 | ||
| CO + H2O = CO2 + H2 | ||
| CH3OH + NH3 = CH3NH2 + H2O | ||
| H2 + O2 = 2H2O | ||
| C6H6 + 3H2 = C6H12 | ||
| C2H6 = C2H4 + H2 | ||
| C2H5OH = CH3COH + H2 | ||
| C2H4(г) + H2O(г) = C2H5OH(г) | ||
| C2H5OH = C2H4 + H2O | ||
| C4H8 = C2H4 | ||
| CH3OH + CO = CH3COOH | ||
| 2NO = N2 + O2 | ||
| C4H10 = C4H8 + H2 бутан бутен | ||
| 2H2S = 2H2 + S2(г) | ||
| FeO(кр) + H2 = Fe(кр) + H2O(г) | ||
| Fe3O4(кр) + H2 = 3FeO(кр) + H2O(г) | ||
| N2 +C2H2 = 2HCN | ||
| CH4 + H2O(г) = CO + 3H2 | ||
| CCl4(г) + 2H2O(г) = CO2 +3H2 | ||
| C(гр) + CO2 = 2CO | ||
| HCOOH(г) = CO2 +H2 | ||
| Fe2O3(кр) +СO = 2FeO(кр) + CO2 | ||
| CO + H2 = C(кр) + H2O(г) | ||
| 2NO + O2 = 2NO2 | ||
| 2CO + O2 = 2CO2 | ||
| 2H2S + 3O2 = 2H2O(г) +2SO2 | ||
| 2ZnS(кр) + 3O2 = 2ZnO(кр) + 2 SO2 | ||
| 4NH3(г) + 3O2 = 2N2 + 6H2O(г) |
Таблица 1.4 Термодинамические характеристики веществ
| Вещество | DН0обр 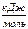 | S0, 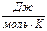 | ср = а + bT + 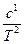 + сТ2, + сТ2, 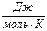 | 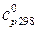 , , 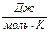 | |||
| а | b ∙ 10-3 | c ∙ 10-6 | c' ∙ 105 | ||||
| H2(г) | 130,7 | 27,3 | 3,27 | - | 0,5 | 28,85 | |
| O2 (г) | 205,2 | 31,46 | 3,39 | - | -3,77 | 29,37 | |
| N2 (г) | 191,5 | 27,87 | 4,27 | - | - | 29,14 | |
| Cl2 (г) | 223,1 | 36,9 | 1,05 | - | -2,52 | 33,96 | |
| H2O (г) | -242,0 | 188,9 | 30,02 | 10,72 | - | 0,33 | 33,6 |
| CO(г) | -110,6 | 197,7 | 28,43 | 4,1 | - | -0,46 | 29,13 |
| CO2 (г) | -393,51 | 213,8 | 44,17 | 9,04 | - | -8,54 | 37,14 |
| NO (г) | 90,3 | 210,7 | 29,58 | 3,85 | - | -0,58 | 29,89 |
| NO2 (г) | 33,89 | 240,3 | 42,16 | 8,54 | - | -6,74 | 37,11 |
| N2O4 (г) | 9,37 | 304,0 | 83,89 | 39,75 | - | -14,90 | 78,99 |
| NH3 (г) | -46,19 | 192,5 | 29,80 | 25,48 | - | -1,67 | 35,65 |
| HCl (г) | -92,4 | 186,9 | 26,54 | 4,61 | - | 1,09 | 29,15 |
| CH4 (г) | -74,9 | 186,4 | 17,46 | 60,5 | 1,118 | - | 35,63 |
| С2Н2(г) | 226,75 | 200,82 | 26,44 | 66,65 | -26,48 | - | 43,93 |
| С2H4 (г) | 52,28 | 219,4 | 4,19 | 154,59 | -81,09 | - | 43,63 |
| C2H6 (г) | -84,67 | 229,7 | 4,494 | 182,26 | -74,86 | - | 52,71 |
| С4Н8(г) 1-бутен | -0,13 | 305,60 | 21,47 | 258,40 | -80,84 | - | 85,65 |
| С4Н10(г) бутан | -126,15 | 310,12 | 18,23 | 303,56 | -92,65 | - | 97,45 |
| C6H6 (г) | 82,93 | 269,2 | -33,90 | 471,87 | -298,34 | - | 81,67 |
| C6H12 (г) | -123,2 | 298,4 | -51,75 | 598,87 | -230,0 | - | 106,34 |
| CH3OH (г) | -202,1 | 239,9 | 15,29 | 105,27 | -31,07 | - | 44,00 |
| CH3CHO (г) | -166,0 | 264,2 | 13,02 | 153,51 | -53,72 | - | 54,64 |
| СН3СОСН3(г) | -217,57 | 294,93 | 14,82 | 196,70 | -77,70 | - | 74,90 |
| C2H5OH (г) | -235,3 | 282,0 | 19,09 | 212,86 | -108,69 | - | 73,6 |
| CCl4(г) | -100,42 | 310,12 | 59,36 | 97,00 | -49,57 | - | 83,76 |
| NH4Cl (т) | -315,4 | 94,56 | 49,37 | 133,89 | - | - | 84,20 |
| Mg(OH)2(т) | -924,66 | 63,2 | 54,56 | 66,15 | - | - | 76,99 |
| MgO (т) | -601,24 | 26,94 | 42,59 | 7,28 | - | -6,20 | 37,41 |
| CaCO3 (т) | -1207,9 | 92,9 | 104,5 | 21,92 | - | -25,94 | 81,85 |
| CaO (т) | -635,5 | 39,8 | 49,65 | 4,52 | - | -6,95 | 42,83 |
| Ca(OH)2 (т) | -986,8 | 83,4 | 105,27 | 11,953 | - | -18,979 | 87,55 |
| S2 (г) | 129,1 | 228,2 | 36,11 | 1,09 | - | -3,52 | 32,49 |
| SO2 (г) | -296,9 | 248,2 | 42,55 | 12,55 | - | -5,65 | 39,90 |
| SO3 (г) | -395,2 | 256,23 | 57,36 | 26,88 | - | -13,06 | 50,70 |
| SO2Cl2 (г) | -358,7 | 311,3 | 53,72 | 79,50 | - | - | 77,4 |
| COCl2 (г) | -223,0 | 289,2 | 67,16 | 12,11 | - | -9,03 | 60,67 |
ХИМИЧЕСКОЕ РАВНОВЕСИЕ
Большая часть химических реакций обратима. Обратимые реакции – реакции, которые при определенных условиях протекают одновременно в двух направлениях: прямом и обратном. Термодинамически химическое равновесие определяется как такое соотношение концентраций исходных веществ и продуктов реакции, при котором энтропия имеет максимальное, а свободная энергия – минимальное значения.
Константа равновесия химической реакции зависит от природы и температуры и не зависит от концентрации реагирующих веществ. Для реакции:
mA + nB ↔ pC +qD
константа равновесия определяется из следующего уравнения:
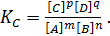 (2.1)
(2.1)
Уравнение (2.1) выражает закон действующих масс: в состоянии равновесия отношение произведений концентраций продуктов реакции к произведению концентраций исходных веществ есть величина постоянная. При этом степени концентраций равны коэффициентам перед формулами данных веществ или элементов.
Концентрации газообразных веществ можно заменить соответствующими парциальными давлениями, при этом константа равновесия обозначается Kp.
Константы Kc и Kp для одной и той же реакции численно равны между собой, но между ними существует определенная зависимость:
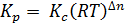 , (2.2.)
, (2.2.)
где Δn – приращение числа молей газообразных веществ.
Для определения направления реакции при изменении одного или нескольких факторов равновесия необходимо руководствоваться принципом Ле-Шателье: если на систему, находящуюся в равновесии, оказать внешнее воздействие (изменить температуру, давление или концентрацию), то в ней произойдут изменения, противодействующие этому воздействию и стремящиеся восстановить первоначальные условия.
Константа равновесия связана с Δr G0 химической реакции:
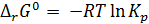 . (2.3)
. (2.3)
Изменение ΔrG или ΔrF в химической реакции при заданных (не обязательно равновесных) парциальных давлениях pi или ci концентрациях реагирующих веществ можно рассчитать по уравнению изотермы химической реакции (изотермы Вант-Гоффа):
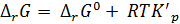 . (2.4)
. (2.4)
Величину K’p, иногда, называют «константой неравновесия» по аналогии с константой равновесия Kp, так как она тоже выражается через парциальные давления, однако, неравновесные.
Зависимость константы равновесия от температуры описывается уравнением изобары химической реакции (изобары Вант-Гоффа)
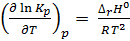 (2.5)
(2.5)
и изохоры химической реакции (изохоры Вант-Гоффа)
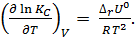 (2.6)
(2.6)
Разделяя переменные в уравнениях (2.5) и (2.6) и интегрируя при ΔH = const (или ΔU = const), получаем:
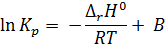
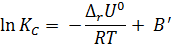
где В и В’ – некие константы.
Интегрируя в пределах K1, K2 и T1, T2, получим:
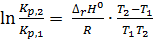 , (2.7)
, (2.7)
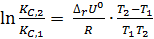 .
.
По этому уравнению, зная константы равновесия при двух разных температурах, можно рассчитать ΔrH реакции. Соответственно, зная ΔrH реакции и константу равновесия при одной температуре, можно рассчитать константу равновесия при другой температуре.
Литература:[1], с. 79 – 87; [2], с. 92 – 103.
Примеры решения задач
Пример 2.1Обратимая химическая реакция протекает по уравнению:
A +2B ↔ C.
При установившемся равновесии концентрации участвующих в реакции веществ составили: [A] = 0,6 моль/л; [B] = 1,2 моль/л; [C] = 2,16 моль/л. Определите исходные концентрации веществ A и B.
Решение: Константу равновесия определяем по уравнению (2.1)
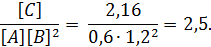
Согласно уравнению реакции, из 1 моль А и 2 моль В образуется 1 моль С. Из сказанного следует, что на образование каждых 2,16 моль С потребуется 2,16 моль А и 2,16∙2 = 4,32 моль В.
Таким образом, исходные концентрации веществ А и В, т.е. число молей веществ А и В на каждый литр смеси до начала реакции, составляли
[A] = 0,6 ∙ 2,16 = 2,76 моль/л,
[B] = 1,2 ∙4,32 = 5,52 моль/л.
Ответ:[A] =2,76 моль/л, [B] = 5,52 моль/л.
Пример 2.2 Для реакции
N2(г) + 3H2(г) = 2NH3(г)
при 298 К Kp = 6,0 ∙ 105, а 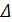 fH0(NH3) = -46,1 кДж/моль. Оцените значение константы равновесия при 500 К.
fH0(NH3) = -46,1 кДж/моль. Оцените значение константы равновесия при 500 К.
Решение: Стандартная мольная энтальпия реакции равна
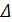 rH0 =
rH0 = 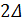 fH0 (NH3) = -92,2 кДж/моль.
fH0 (NH3) = -92,2 кДж/моль.
Согласно уравнению (2.7),
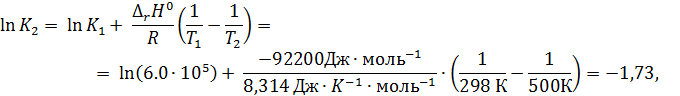
откуда К2 = 0,18.
Ответ:К2 = 0,18.
Контрольные задания
Указание: во всех задачах считать газы идеальными.
81 Закон действия масс. Константы равновесия и связь между ними. Зависимость констант равновесия от температуры.
82 Смещение химического равновесия. Влияние температуры, давления и концентрации на химическое равновесие.
83 Изотерма Вант-Гоффа. Изменение энергии Гиббса и энергии Гельмгольца при химической реакции.
84 Уравнения изобары и изохоры реакции и их термодинамический вывод.
85 Связь константы химического равновесия с максимальной работой реакции.
86 Гетерогенные химические равновесия и особенности их термодинамического описания.
87 Реакция между веществами А и В выражается уравнением
А + 2В = С.
Начальная концентрация вещества А равна 0.3 моль/л, а вещества В – 0,5 моль/л. Константа скорости реакции равна 0,4. Определить начальную скорость реакции и скорость реакции по истечении некоторого времени, когда концентрация вещества А уменьшится на 1,0 моль.
88 При нагревании смеси углекислого газа и водорода в закрытом сосуде устанавливается равновесие. Константа равновесия реакции
CO2 + H2 ↔ CO + H2O
при температуре 850°С равна единице. Сколько процентов углекислого газа превратится в окись углерода, если смешать 1 моль углекислого газа и 4 моль водорода?
89 При температуре 3000°С 40% двуокиси углерода диссоциирует по уравнению
2CO2 ↔ 2CO + O2.
Определить Kp при этой температуре.
90 Определить константу равновесия реакции
CO + H2O ↔ CO2 + H2
при температуре 1000 К на основании следующих данных:
| H2 | H2O | CO | CO2 | |
| ΔН°(кал/моль) | ||||
| ΔS° (кал/град∙моль) | 31,211 | 45,106 | 47,301 | 51,06 |
ΔСp = 1,72 кал/моль.
91 При 693 К константа равновесия реакции H2 + I2 = 2HI Кс = 50,25. Вычислите массу образующегося иодида водорода, если в реактор введено 0,846 г I2 и 0,0212 г Н2.
92 При 693 К константа равновесия реакции H2 + I2 = 2HI КС = 50,25. В каком направлении будет протекать данный процесс, если исходные концентрации Н2 , I2 и HI соответственно равны: а) 2,0; 5,0; 10,0 моль/л; б) 1,5; 0,25; 5,0 моль/л; в) 1,0; 1,99; 10,0 моль/л.
93 Определите константу равновесия реакции SO2 + 1/2O2 = SO3 при 700 К, если при 500 К Кр = 588,9 Па-1/2, а тепловой эффект реакции в этом диапазоне температур равен –99,48 кДж/моль.
94 При 2000 °С и общем давлении 1 атм 2 % воды диссоциировано на водород и кислород. Рассчитайте константу равновесия реакции Н2О(г) = Н2(г) + 1/2О2(г) при этих условиях.
95 Константа равновесия реакции СО(г) + Н2О(г) = СО2(г) + Н2(г) при 500 °С равна Кр = 5,5. Смесь, состоящую из 1 моль СО и 5 моль Н2О, нагрели до этой температуры. Рассчитайте мольную долю Н2О в равновесной смеси.
96 Константа равновесия реакции N2O4(г) = 2NO2(г) при 25 °С равна Кр = 0,143. Рассчитайте давление, которое установится в сосуде объемом 1 л, содержащем 1 г N2O4 при этой температуре.
97 Сосуд объемом 3 л, содержащий 1,79∙10-2 моль I2, нагрели до 973 К. Давление в сосуде при равновесии оказалось равно 0,49 атм. Считая газы идеальными, рассчитайте константу равновесия при 973 К для реакции I2(г) = 2I(г).
98 Сосуд объемом 1 л, содержащий 0,341 моль РCl5 и 0,233 моль N2, нагрели до 250 °С. Общее давление в сосуде при равновесии оказалось равно 29,33 атм. Считая все газы идеальными, рассчитайте константу равновесия при 250 °С для протекающей в сосуде реакции: РСl5(г) = РСl3(г) + Сl2(г).
99Для реакции 2HI(г) = H2(г) + I2(г) константа равновесия Кр = 1,83∙10-2 при 698,6 К. Сколько граммов HI образуется при нагревании до этой температуры 10 г I2 и 0,2 г H2 в трехлитровом сосуде? Чему равны парциальные давления H2, I2 и HI?
100Константа равновесия реакции H2(г) + I2(г) = 2HI(г) при 717 К равна 46,7. Определите количество разложившегося HI при нагревании 1 моль HI до этой температуры.
101Константа равновесия реакции CO(г) + H2O(г) = CO2(г) + H2(г) при 800 К равна 4,12. Смесь, содержащая 20 % СO и 80 % Н2О нагрета до 800 К. Определите состав смеси при достижении равновесия, если взят 1 кг водяного пара.
102При 1273 К и общем давлении 30 атм в равновесной смеси СO2 (г) + С(тв) = = 2СО(г) содержится 17 % (по объему) СО2. Сколько процентов СО2 будет содержаться в газе при общем давлении 20 атм?
103 При смешении 1 моль уксусной кислоты и 1 моль этилового спирта реакция протекает по уравнению CH3COOH(г) + C2H5OH(г) = CH3COOC2H5(г) + H2O(г). При достижении равновесия в реакционной смеси находится 1/3 моль кислоты, 1/3 моль спирта, 2/3 моль эфира и 2/3 моль воды. Вычислите количество моль эфира, которое будет в реакционной смеси по достижению равновесия при следующих условиях: 1 моль кислоты, 1 моль спирта и 1 моль воды.
104-123 Многовариантная задача. Вычислите величину константы равновесия при заданной температуре Т. Примите, что тепловой эффект реакции в этом температурном интервале не зависит от температуры. Примечание: если агрегатные состояния не указаны, вещества находятся в газовой фазе.
Таблица 2.1 Уравнения реакций для различных вариантов
| № п/п | Реакция | Т, К | КТ1 | КТ2 | 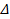 H0 , кДж/ моль H0 , кДж/ моль |
| 2СО + 4Н2= С2Н5ОН + Н2О | 7,0∙10-8 (Т1 = 400 К) | 8,4∙10-8 (Т2 = 500 К) | - | ||
| 2HgO(тв) = 2Hg + О2 | 1,37∙1014 (Т1 = 693 К) | - | |||
| Ag2CO3(тв) =Ag2O(тв) + CO2 | 3,98∙10-4 (Т1 = 350 К) | 1,86∙10-4 (Т2 = 450 К) | - | ||
| 2СН3ОН = С2Н4 + 2Н2О | 1,9 (Т1 = 700 К) | 5,57 (Т2 = 1000 К) | - | ||
| 2C3H6 = C2H4 + C4H8 | 5,03∙10-2 (Т1 = 300 К) | 8,77∙10-2 (Т2 = 600 К) | - | ||
| Hr(aq) + O2 = HrO2(aq) (Hr – гемеритрин, кислородпереносящий пигмент) | (Т1 = 273 К) | (Т2 = 298 К) | - | ||
| СН3ОН = НСНО + Н2 | 6,1∙10-4 (Т1 = 700 К) | 5,6∙10-4 (Т2 = 500 К) | - | ||
| 4HCl + O2 = 2H2O + Cl2 | 6,72∙10-4 (Т1 = 700 К) | 3,96∙10-6 (Т2 = 900 К) | - | ||
| С3Н6 + 3/2О2 = СН3СНО + НСООН | 9,1∙1015 (Т1 = 600 К) | - | 168,15 | ||
| NH4Cl(тв) = NH3 + HCl | 3,80∙107 (Т1 = 400 К) | 1,81∙1012 (Т2 = 500 К) | - | ||
| СО + 2Н2 = СН3ОН | 3,88∙10-11 (Т1 = 400 К) | - | 113,13 | ||
| Mg(OH)2 (тв) = MgO(тв) + H2O | 7,26∙105 (Т1 = 350 К) | 5,59∙109 (Т2 = 500 К) | - | ||
| 2C5H11 + 2H2 = 2C4H10 +C2H6 | 1,46 (Т1 = 373 К) | - | 3,18 | ||
| S2 + 4CO2 = 2SO2 + 4CO | 1,58∙1011 (Т1 = 850 К) | 3,39∙1011 (Т2 = 950 К) | - | ||
| SO2 + Cl2 = SO2Cl2 | 8,51∙10-6 (Т1 = 350 К) | 2,27∙10-7 (Т2 = 450 К) | - | ||
| C6H6 + 3H2 = C6H12 | 9,54∙10-6 (Т1 = 350 К) | 2,30∙10-6 (Т2 = 450 К) | - | ||
| H2 + Cl2 = 2HCl | 3,25∙1011 (Т1 = 900 К) | 2,67∙1010 (Т2 = 1000 К) | - | ||
| H2 + I2 = 2HI | 61,6 (Т1 = 633 К) | 41,7 (Т2 = 718 К) | - | ||
| C6H5C2H5 + 3H2 = C6H11C2H5 | 5,98∙10-14 (Т1 = 485 К) | 9,30∙10-17 (Т2 = 565 К) | - | ||
| I2 = 2I | 1,15∙102 (Т1 = 950 К) | 7,41∙102 (Т2 = 1050 К) | - |
ФАЗОВЫЕ РАВНОВЕСИЯ
Общие закономерности, которым подчиняются равновесные системы, содержащие любое число фаз и компонентов, устанавливаются правилом фаз Гиббса, согласно которому
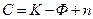 , (3.1)
, (3.1)
где К – число компонентов системы, Ф – число фаз, n – число внешних факторов, определяющих существование системы (p, T, c), С – число степеней свободы, показывающая число переменных, которым можно придавать произвольные значения, не изменяя число фаз.
Количественно условие равновесия фаз в однокомпонентных системах выражается уравнением Клаузиуса:
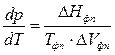 , (3.2)
, (3.2)
где 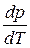 - производная, описывающая изменение давления пара над жидкостью или твердым телом при испарении или возгонке;
- производная, описывающая изменение давления пара над жидкостью или твердым телом при испарении или возгонке; 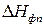 - молярная теплота равновесного фазового перехода при температуре
- молярная теплота равновесного фазового перехода при температуре 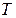 и давлении
и давлении 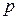 ;
; 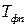 - температура фазового перехода;
- температура фазового перехода; 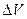 - изменение объема одного моля вещества при фазовом переходе.
- изменение объема одного моля вещества при фазовом переходе.
Интегрирование уравнения Клаузиуса из предположения 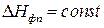 для равновесия газ-жидкость и газ-твердое тело приводит к уравнению Клаузиуса-Клапейрона:
для равновесия газ-жидкость и газ-твердое тело приводит к уравнению Клаузиуса-Клапейрона:
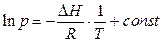 . (3.3)
. (3.3)
Поэтому для системы газ-жидкость тангенс угла наклона зависимости ln р =f( 1/Т) дает значение 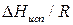 , а для системы газ-твердое тело – значение
, а для системы газ-твердое тело – значение 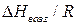 . Точка пересечения этих прямых дает координаты тройной точки.
. Точка пересечения этих прямых дает координаты тройной точки.
Температуру кипения Ткип вещества при нормальном давлении определяют по формуле, полученной из уравнения Клаузиуса-Клапейрона:
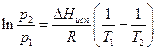 . (3.4)
. (3.4)
Для проверки применимости правила Трутона к данной системе необходимо найти отношение 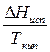 . Если оно отличается от значения 89
. Если оно отличается от значения 89 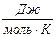 , то правило Трутона не применимо.
, то правило Трутона не применимо.
Взаимосвязь параметров в равновесной системе газ-твердое тело выражается уравнением:
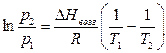 . (3.5)
. (3.5)
Теплоту плавления вещества 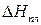 при температуре тройной точки определяют исходя из теплоты возгонки и теплоты испарения:
при температуре тройной точки определяют исходя из теплоты возгонки и теплоты испарения:
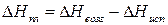 . (3.6)
. (3.6)
Параметры процесса возгонки определяют по следующим формулам:
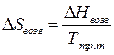 , (3.7)
, (3.7)
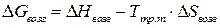 , (3.8)
, (3.8)
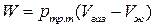 , (3.9)
, (3.9)
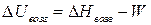 (3.10)
(3.10)
Литература:[1], с. 70 – 78, 88-112; [2], с. 65 – 91.
Примеры решения задач
Пример 3.1 Определить число степеней свободы системы
CaCO3 ↔ CaO + CO2
Решение: В системе существуют три фазы: две твердые – CaCO3 и CaO – и одна газообразная – CO2. Так как из двух фаз системы CaO и CO2 может быть получена третья фаза – CaCO3, то число независимых компонентов равно 2.
На основании уравнения правила фаз (3.1) определим число степеней свободы:
С = К – Ф +2 = 2-3+2 =1.
Таким образом, произвольно можно менять в определенных пределах только один фактор равновесия, например, температуру.
Контрольные задания
124 Гетерогенные системы. Компонент, фаза, число степеней свободы системы. Правило фаз Гиббса.
125 Уравнение Клаузиуса. Применение данного уравнения для описания процессов плавления, испарения, возгонки.
126 Однокомпонентные гетерогенные системы. Фазовая диаграмма воды.
127 Однокомпонентные гетерогенные системы. Фазовая диаграмма серы.
128 Закон Рауля для смеси летучих жидкостей. Положительные и отрицательные отклонения от закона Рауля.
129 Разделение неограниченно смешивающихся жидкостей с помощью фракционной перегонки. 1-ый закон Коновалова.
130 Азеотропные смеси. 2 –ой закон Коновалова. Методы разделения азеотропных смесей.
131 Диаграмма состояния двухкомпонентной системы с ограниченной растворимостью в жидкой фазе. Критическая температура растворимости. Правило Алексеева. Правило рычага.
132 Несмешивающиеся жидкости. Перегонка с водяным паром.
133 Фазовая диаграмма состояния трехкомпонентной системы с неограниченно смешивающимися компонентами. Использование метода Гиббса и Розебума для определения состава системы.
134 Молярная теплота испарения воды равна 43,09 кДж/моль. Давление насыщенного водяного пара при температуре 40 °С равно 55,3 мм рт.ст. Чему равно давление насыщенного пара при температуре 50 °С?
135 Давление паров над жидким галлием при температуре 1029 °С равно 0,01 мм рт.ст. , а при 1154 °С - 0,1 мм рт.ст. Чему равна молярная теплота испарения галлия?
136 Молярная энтальпия плавления льда равна 6,01 кДж/моль, а энтальпия испарения воды 41,09 кДж/моль. Чему равна молярная энтальпия возгонки льда?
137 Давление пара над серной кислотой при температуре 451 К равно 666Па, а при температуре 484,5 К - 2666 Па. Определите теплоту парообразования серной кислоты, считая ее постоянной в указанном интервале температуры.
138 Зависимость давления (Па) насыщенного пара над жидким TiCl4 описывается уравнением ln p = 19,688 – 3335/Т. Рассчитайте энтальпию и энтропию парообразования одного моля тетрахлорида титана при нормальной температуре кипения.
139 Под давлением 0,1013 МПа лед плавится при 273К. Удельный объем льда при 273 К равен 991,1 см3/кг, а воды – 916,6 см3/кг. Молярная теплота плавления льда равна 6010 Дж/моль. Вычислите давление, при котором лед будет плавиться при 271 К.
140 Плотности жидкого и твердого олова при температуре плавления (231,9 °С) равны 6,980 г/см3 и 7,184 г/см3, соответственно. Энтальпия плавления олова равна 1, 690 ккал/моль. Определите температуру олова под давлением 500 атм. Молярная масса олова равна 118,7 г/моль.
141 При замерзании бензола (5,5 °С) его плотность изменяется от 0,879г/см3 до 0, 891 г/см3. Энтальпия плавления равна 10,59 кДж/моль. Определите температуру плавления бензола при давлении 1000 атм.
142 Плотности жидкой и твердой ртути при температуре плавления (-38,87 °С) равны 13,690 и 14,193 г/см3, соответственно. Энтальпия плавления ртути равна 2,33 кал/г. Определите температуру плавления ртути при давлении 3000 атм.
143 Температура кипения жидкого метанола равна 34,7 °С при давлении 200 Торр и 49,9 °С при давлении 400 Торр. Найдите температуру кипения метанола при нормальном давлении.
144 Давление пара диэтилового эфира при 10 °С равно 286,8 Торр, а при 20 °С – 432,8 Торр. Определите мольную энтальпию испарения и нормальную температуру кипения эфира.
145 Давление пара дихлорметана при 24,1 °С равно 400 Торр, а его энтальпия испарения равна 28,7 кДж/моль. Рассчитайте температуру, при которой давление пара будет равно 500 Торр.
