Стандартные электродные потенциалы

Абсолютное значение разности потенциалов на границе двух фаз разной природы металл│электролит измерить нельзя, однако можно измерить электродвижущую силу (ЭДС, Е_ГЭ) гальванического элемента, которая определяется

разностью электродных потенциалов полуэлементов составляющих редокс – систему

Если электродный потенциал одного из электродов,

выбранного эталонным, принять за нуль, то электродный потенциал другого будет равен ЭДС этого гальванического элемента.

Таким эталонным электродом был выбран водородный электрод в стандартных условиях.

Его устройство таково: платиновый электрод, покрытый мелкодисперсной платиной (платиновой чернью), погруженный в раствор серной кислоты с активностью ионов водорода 1 моль×л^–1, обдувается струей газообразного водорода под давлением 1,013×10⁵Па.

Платиновая чернь адсорбирует водород, который электрохимически взаимодействует с раствором по уравнению:

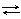H_2(газ) 2H⁺ + 2

Таким образом, стандартный электродный потенциал 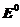(вольт, В) – численно равен ЭДС гальванического элемента, содержащего в качестве электрода сравнения стандартный водородный электрод, а в качестве другого электрода − измеряемый электрод при активностях всех реагентов окислительно-восстановительного процесса, равных 1 моль/л, и температуре 298 К

(–) Pt , H₂ |2H⁺ ||Mⁿ⁺ |M (+).

При измерении стандартных электродных потенциалов редокс-систем водородный электрод сравнения всегда занимает место анода (восстановителя), измеряемые электроды − место катода (окислителя).

_{Электрод сравнения Измеряемый электрод}

(–) Pt , H₂ |2H⁺ ||о.ф.о.|в.ф.о. (+) ,т.е.

На исследуемом электроде (катоде) происходит полуреакция восстановления: о.ф.о + nē → в.ф.о.

Измеренные таким образом стандартные электродные потенциалы Е⁰_{о.ф.о./в.ф.о.} отражают катодную реакцию и характеризуют окислительную способность (присоединять ē) измеряемого электрода. Полученные экспериментальные значения имеют знаки плюс (например, Е _Си²⁺/_Си = + 0,34 В) и минус (E⁰_Zn²⁺/_Zn = -0,76 B).

Знак (-) говорит о том, что данный электрод не проявляет по отношению к водородному электроду окислительных свойств и, стало быть, в приведенном примере пара Zn│Zn²⁺ фактически является анодом (восстановителем). В общем случае электрод с относительно более положительным значением стандартного электродного потенциала является окислителем по отношению к электроду с менее положительным значением Е⁰, и в гальваническом элементе он будет играть роль катода (раздел 7.5.).

Чем больше электродный потенциал, тем сильнее выражены окислительные свойства данной электродной пары.

Чем больше разница в электродных потенциалах катода и анода, тем выше ЭДС (Е_ГЭ): Е_ГЭ = Е _кат – Е _ан

Все стандартные электродные потенциалы сведены в таблицы и содержат в себе катодные реакции.

Значения некоторых стандартных электродных потенциалов в порядке их возрастания, представлены в табл. 7.1.

Уравнение Нернста

Поскольку реальные растворы электролитов могут иметь самые разные концентрации и активности, влияющие на электродный потенциал, необходимо это учитывать при работе в нестандартных условиях. Зависимость электродного

потенциала от активностей ионов в растворе и от температуры описывается уравнением Нернста.

Выведем эту зависимость на примере гальванического элемента, состоящего из стандартного водородного и медного электрода с произвольной концентрацией Сu²⁺.

(–) Pt , H₂ |2H⁺ ||Cu²⁺ |Cu (+) .

Реакции на аноде и катоде:

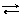
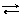(-): H_2(газ) - 2 2H⁺ (+): Сu²⁺+ 2 ē Cu

Т а б л и ц а 7.1

Стандартные электродные потенциалы, E⁰, B

Окисленная форма	+ n	Восстановленная форма	E0, B
Na+	1	Na	–2,71
Zn2+	2	Zn	–0,76
Cr3+	3	Cr	–0,74
Fe(OH)3	1	Fe(OH)2 + OH–	–0,53
Fe2+	2	Fe	–0,44
Cd2+	2	Cd	–0,40
PbSO4	2	Pb +SO42–	–0,359
Co2+	2	Co	–0,29
Ni2+	2	Ni	–0,23
Sn2+	2	Sn	–0,14
Pb2+	2	Pb	–0,13
2H+	2	H2	0,00
NO3-+H2O	2	NO2-+2OН-	+0,01
Ti4+	1	Ti3+	+0,04
Sn4+	2	Sn2+	+0,15
SO42-+2H+	2	SO32-+H2O	+0,17
Cu2+	2	Cu	+0,34
[Fe(CN)6]3-	1	[Fe(CN)6]4-	+0,358
Ni(OH)3	1	Ni(OH)2 +OH–	+0,49
I2	2ē	2I-	+0,54
MnO4-	1	MnO42-	+0,56
MnO4-+2H2O	3	MnO2+4OH-	+0,60
Fe3+	1	Fe2+	+0,77
Ag	1	Ag+	+0,80
NO3-+4H+	3	NO+2H2O	+0,96
Br2	2	2Br-	+1,07
Cl2	2	2Cl-	+1,36
Cr2O72-+14H+	6	2Cr3++7H2O	+1,37
MnO4-+8H+	5	Mn2++4H2O	+1,51
H2O2+2H+	2	2H2O	+1,77
PbO2+SO42-+4H+	2	PbSO4+2H2O	1,685

Для суммарной токообразующей реакции:

Сu²⁺ + H₂ Cu + 2H⁺запишем уравнение изотермы Вант-Гоффа 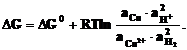(7.1)

Энергиия Гиббса (DG) токообразующей реакции cвязана с ЭДС ГЭ формулой:DG = – nFE,

где F - число Фарадея1⁾, равное 96500 Кл/моль;

n - число (моль) электронов, участвующих в электрохимическом процессе.

Вывод этой зависимости основан на следующих положениях:

1. ХИТ обычно работают в изобарно-изотермических условиях (т. е. при постоянных давлении р и температуре Т). Для этих условий максимально возможная работа, которая может быть получена в системе при обратимом протекании химической реакции А_max, равна уменьшению свободной энергии (энергии Гиббса, ΔG) системы для этой реакции:

А_max = -∆G (7.2)

2. С другой стороны, максимальная работа, которую можно получить от гальванического элемента, A_ГЭmax равна произведению ЭДС элемента Е_ГЭ на количество электричества q_ГЭ:

A_ГЭmax = Е_ГЭ∙q_ГЭ (7.3)

По объединенному закону Фарадея при электрохимическом превращении вещества через систему протекает количество электричества, равное произведению числа молей электронов n на число Фарадея F, т,е.

q = n∙F (7.4)

Приравнивая максимальную работу химической реакции (7.2) и максимальную электрическую работу (7.3) с учетом (7.4)), получим нужную формулу: DG = – nFE.

Подставим в уравнение (7.1) вместо DG равную величину (– nFE) и разделим обе части на (– nF).

Далее введём в уравнение численные значения F, R и T=298K и перейдём от натуральных логарифмов к десятичным. С учётом того, что для стандартного водородного электрода активности ионов H⁺и газа H₂ равны 1, а 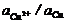= 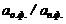, _.получим удобную для расчётов общепринятую форму уравнения Нернста для отдельного электрода, отражающего зависимость электродного потенциала от концентраций (активностей) реагентов.

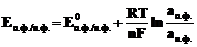, (7.5)

Принятая запись E_о.ф./_в.ф. соответствует условиям, при которых определялись стандартные электродные потенциалы, т.е. катодной реакции: о.ф. → в.ф. (Сu²⁺ → Cu).

Активность твердого вещества принимается равной единице, поэтому в случае рассматриваемого нами металлического медного электрода уравнение Нернста упрощается:

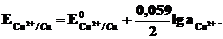
Вещества, входящие под знак логарифма, являются потенциалопределяющими, а электрод считается обратимым по отношению к соответствующему иону.

Так, в медном электроде катионы Сu²⁺ будут потенциалопределяющими, а электрод обратим по отношению к катиону.

Подведём некоторые итоги:

− уравнение Нернста для отдельного электрода условились писать для процесса восстановления (+ nē) независимо от того, в какую сторону сдвинуто равновесие, то есть под знаком логарифма в уравнении Нернста в числителе стоит окисленная форма реагента, в знаменателе – восстановленная.

− в дробном индексе при E и E⁰ над чертой ставится окисленная форма реагента, под чертой – восстановленная.

− активности твердых веществ в уравнение Нернста не входят.

Типы электродов

Многочисленные ХИТ могут быть составлены из двух электродов (полуэлементов, электродных пар). По типу потенциалопределяющей реакции (окислительно-восстанови-тельного электродного процесса) электроды делят на первого и второго рода - электроды с электрохимической реакцией) и ионоселективные - без электрохимической реакции.

К электродам первого родаотносятся электроды, в уравнение Нернста которых под знак логарифма входят активности веществ, участвующих в электродном процессе. Потенциал таких электродов меняется с изменением концентрации реагентов.

Электродами первого рода являются:

1. Электроды, состоящие из элементарного вещества, находящегося в контакте с раствором, содержащим его собственные ионы.

а) Металлический электрод– металл, погруженный в раствор своей соли М½Мⁿ⁺, например, цинковый и медный электроды:

Zn½Zn²⁺ Zn Zn²⁺ + 2

Cu½Cu²⁺ Cu Cu²⁺ + 2 .

Металлический электрод обратим по отношению к катиону. Его электродный потенциал

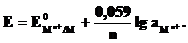
б) Газовый электрод в качестве одного из компонентов электродной пары содержит газ (H₂, Cl₂и др.), адсорбированный на химически инертном проводнике первого рода (обычно платина, покрытая платиновой чернью). При контакте адсорбированного газа с раствором собственных ионов устанавливается равновесие. Для хлорного и водородного электродов это равновесие можно представить уравнениями:

Cl₂ + 2 = 2Cl^-; 2H⁺ + 2 = H₂.

Соответствующие им уравнения Нернста имеют вид:

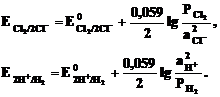
Очевидно, что их электродный потенциал зависит от давления в газовой фазе и активности (концентрации) ионов в растворе. Если давление водорода в газовой фазе поддерживать постоянным и равным 101,325кПа последнее уравнение преобразуется в:

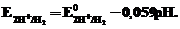
2. Редокс-электродысостоят из инертного по отношению к данному электролиту проводника первого рода (платина, графит и т.д.), погруженного в раствор, в котором находятся одновременно окисленная и восстановленная формы потенциалопределяющего вещества. Такой инертный проводник способствует передаче электронов от восстановителя к окислителю через внешнюю сеть.

Примером редокс-электродов с ионами в различных степенях окисления являются

Pt│ Sn⁴⁺, Sn²⁺; Pt│ Fe³⁺, Fe²⁺

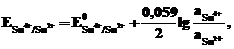
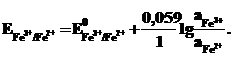
Электроды второго рода представляют собой металлические пластины, покрытые слоем труднорастворимой соли того же металла и опущенные в раствор, содержащий анион этой соли. Его потенциал будет определяться активностью аниона в растворе. Типичным представителемэлектродов второго рода является широко используемый хлорсеребряный электрод.

Хлорсеребряный электрод (ХСЭ) Ag│AgCl½Cl^- представляет собой серебряный проводник, покрытый твердым AgCl,который погружен в насыщенный раствор KСl.

Серебро электрохимически взаимодействует со своим ионом:

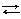Ag⁺ + Ag.

Уравнение Нернста для этого процесса

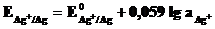. (7.3)

Однако в присутствии КCl активность ионов серебра ничтожно мала, но поскольку она связана с легко задаваемой в данной системе активностью ионов Cl ^-через произведение растворимости хлорида серебра (ПР _AgCl = a_Ag⁺∙a_Cl^-), то её можно представить в виде:

.

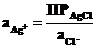Подставим это выражение в (7.3):

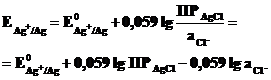
Обозначив ,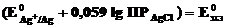

получим уравнение Нернста для хлорсеребряного электрода

.

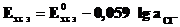Потенциалопределяющими здесь являются ионы хлора, а электродный процесс может быть представлен уравнением:

AgCl_тв + Ag + Cl^-.

В уравнение Нернста для электродов 2 рода под знак логарифма входят концентрации веществ, не участвующих в электродном процессе (не меняют степень окисления).

Электроды второго рода обратимы по отношению к аниону, активность которого в растворе можно поддерживать постоянной, что в свою очередь приводит к постоянству электродного потенциала и даёт возможность использовать эти электроды в качестве электродов сравнения.

Если гальванический элемент составлен из электродов второго рода, он обладает высокой стабильностью, его ЭДС не меняется многие годы

Стеклянный электрод для определения концентрации H⁺ (рН) относится к ионоселективным(мембранным)электродам и состоит из стеклянного тонкостенного шарика (мембраны), припаянного к стеклянной трубке. В шарик налит раствор HCl (внутренний раствор, 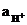=0,1 моль×л^–1), в который опущен хлорсеребряный электрод. При погружении стеклянного электрода в раствор с измеряемой концентрацией H⁺ (внешний раствор) между мембраной и исследуемым раствором происходят процессы ионного обмена, приводящие к возникновению разности потенциалов.

Потенциал стеклянного электрода Ag│AgCl│Cl-, Н+равен

.
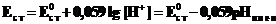