Работа с векторами и матрицами

ПакетMatLab построена как система, ориентирующая на работу с матрицами, то есть все численные вычисления производятся в матричной форме. Система MatLab выполняет сложные и трудоемкие операции над векторами и матрицами даже в режиме прямых вычислений без какого-либо программирования. Ею можно пользоваться как мощнейшим калькулятором, в котором наряду с обычными арифметическими и алгебраическими действиями могут использоваться такие сложные операции, как инвертирование матрицы, вычисление ее собственных значений и принадлежащих им векторов, решение систем линейных уравнений, вывод графиков двумерных и трехмерных функций и многое другое. Важно отметить, что даже обычные числа и переменные в MatLab рассматриваются как матрицы размера 1 x 1, что дает единообразные формы и методы проведения операций над обычными числами и массивами. Это также означает, что большинство функций может работать с аргументами в виде векторов и матриц. При необходимости вектора и матрицы преобразуются в массивы, и значения вычисляются для каждого их элемента.

Массивы являются одним из самых распространенных способов хранения данных и используются во всех языках программирования и математических пакетах. К особенностям работы с массивами в MatLab относится то, что одномерный массив может быть вектор-строкой или вектор-столбцом. Если способ представления массива важен, то мы будем подчеркивать, о строке или о столбце идет речь. Если же это несущественно, то будем говорить о вектор-строках и вектор-столбцах просто как о векторах или одномерных массивах. Напомним, что одномерный массив в MatLab есть двумерный, у которого ода из размерностей равна единице.

Для определения вектора используются квадратные скобки, а элементы вектора отделяются друг от друга:

· точкой с запятой, если требуется получить вектор–столбец;

· пробелом или запятой, если необходимо разместить элементы в векторе-строке.

Пример 3.1-12

>>a=[0.2; -3.9; 4.6] a = 0.2000 -3.9000 4.6000 >>b=[7.6; 0.1; 2.5] b = 7.6000 0.1000 2.5000 >>u=[0.1 0.5 -3.7 8.1] u = 0.1000 0.5000 -3.7000 8.1000 >>v=[5.2 9.7 3.4 –0.2] v = 5.2000 9.7000 3.4000 –0.2000 >>

Получить информацию о переменных, как мы уже знаем, можно с помощью окна Workspace или при помощи команды whos.

Для определения длины вектора используется функция length(а), вектор а указывается в качестве ее входного аргумента.

Пример 3.1-13

>>L=length(a) L = >>

Вектор-столбцы с одинаковым числом элементов можно складывать и вычитать друг из друга при помощи опрераций "+" и "–". Эти правила верны и для вектор-строк.

Сложение и вычитание вектор-строк и вектор-столбцов или векторов разных размеров приводит к ошибке. Операция * предназначена для умножения векторов по правилу матричного умножения. Поскольку MatLab различает вектор-строки и вектор- столбцы, то допустимо либо умножение вектор-строки на такой же по длине вектор-столбец (скалярное произведение), либо умножение вектор-столбца на вектор-строку (внешнее произведение, в результате которого получается прямоугольная матрица). Скалярное произведение двух векторов возвращает функция dot(), а векторное - cross():

Пример 3.1-14

>>s=dot(a, b) s= 1.2630e+001 >>c=cross(a, b) c= -1.0210e+001 3.4460e+001 2.9660e+001 >>

Для операции транспонирования зарезервирован символ апостроф - '. Если вектор содержит комплексные числа, то операция ' приводит к комплексно-сопряженному вектору. При вычислении скалярного и векторного произведений функциями cross() и dot() не обязательно следить за тем, чтобы оба вектора были либо столбцами, либо строками. Результат получается верный, например, при обращении c=cross(a,b'), только c становится вектор-строкой.

MatLab поддерживает поэлементные операции с векторами. Наряду с умножением по правилу матричного умножения, существует операция поэлементного умножения - .* (точка со звездочкой). Данная операция применяется к векторам одинаковой длины и приводит к вектору той же длины, что исходные, элементы которого равны произведениям соответствующих элементов исходных векторов. Например, для векторов a и b, введенных выше, поэлементное умножение дает следующий результат:

Пример 3.1-15

>>c=a.* b c = 1.5200 -0.3900 11.5000 >>

Аналогичным образом работает поэлементное деление - ./(точка с косой чертой). Кроме того, операция .\ (точка с обратной косой чертой) осуществляет обратное поэлементное деление, то есть выражения a./b и b.\a эквивалентны. Возведение элементов вектора a в степени, равные соответствующим элементам b, производится с использованием операции - .^. Для транспонирования вектор-строк или вектор-столбцов предназначено сочетание - .' (точка с апострофом). Операции- ' и .' для вещественных векторов приводят к одинаковым результатам. Не обязательно применять поэлементные операции при умножении вектора на число и числа на вектор, делении вектора на число, сложении и вычитании вектора и числа. При выполнении, например, операции a*2, результат представляет собой вектор того же размера, что и a, с удвоенными элементами.

Векторы могут быть аргументами встроенных математических функций, таких, как sin(), cos() и т. д. В результате получается вектор с элементами, равными значению вызываемой функции от соответствующих элементов исходного вектора, например:

Пример 3.1-16

>>q=sin([0 pi/2 pi]) q = 0 1.0000 0.0000 >>

Однако для вычисления более сложной функции от вектора значений, скажем, 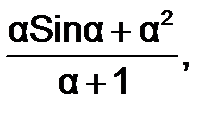где α,например,является вектором-строкой, состоящей из четырех элементов, выражение f=(α*sin(α)+α^2)/(α+1) вызовет ошибку уже при попытке умножения αна sin(α). Дело в том, что αявляется вектор-строкой длиной четыре, то есть хранится в двумерном массиве размером один на четыре. Точно также представлена и функция sin(α), следовательно, умножение при помощи звездочки (по правилу матричного умножения) лишено смысла. Аналогичная ситуация возникает и при возведении вектора α в квадрат, то есть, фактически, при вычислении α*α.

Правильная запись выражения в MatLabтребует использования поэлементных операций.

Пример 3.1-17

>>f=(a.*sin(a)+a.^2)./(a+1); >>

Часто требуется вычислить функцию от вектора значений аргумента, отличающихся друг от друга на постоянный шаг. Для создания таких векторов-строк предусмотрена операция двоеточие - :, которая отделяет начальное значение аргумента, шаг и конечное значение аргумента.

Пример 3.1-18

>>x=-1.2:0.5:1.8 x = -1.2000 -0.7000 -0.2000 0.3000 0.8000 1.3000 1.8000 >>f=(x.*sin(x)+x.^2)./(x+1) f = -12.7922 3.1365 0.0997 0.1374 0.6744 1.2794 1.7832 >>

Шаг может быть отрицательным, в этом случае начальное значение должно быть больше, либо равно конечному значению для получения непустого вектора. Если шаг равен единице, то его можно не указывать, например:

Пример 3.1-17

>>n=-3:4 n = -3 -2 -1 0 1 2 3 4 >>

Ясно, что для заполнения вектор-столбца элементами с постоянным шагом следует транспонировать вектор-строку.

Создание векторов при помощи двоеточия и умение производить поэлементные операции необходимо для визуализации массивов данных.

Пример 3.1-18

>>x=10:-2:0x = 10 8 6 4 2 0>>sin(x)= -0.5440 0.9894 -0.2794 -0.7568 0.9093 0 >>

Необходимо отметить, что при умножении векторов друг на друга получается скаляр.

Пример 3.1-19

>>y=[2 3 5 8 3 9];>>x*y??? Error using ==> * Inner matrix dimensions must agree. >>

Здесь допущена ошибка, так как матрицы (векторы) не согласованны. Правильно будет

Пример 3.1-20a

>>x*y'ans = 112>>

или можно было создать у как матрицу-столбец:

Пример 3.1-20b

>>y=[2;3;5;8;3;9] >>

MatLab обладает большим набором встроенных функций для обработки векторных данных, часть из них приведена в табл. 5.3-6.

Таблица. 3.1-6

Функции	Назначение
s=sum(a)	Сумма всех элементов вектора a
p=prod(a)	Произведение всех элементов вектора a
m=max(a)	Нахождение максимального значения среди элементов вектора a
[m,k]=max(a)	Второй выходной аргумент k содержит номер максимального элемента в векторе a
m=min(a)	Нахождение минимального значения среди элементов вектора a
[m,k]=min(a)	Второй выходной аргумент k содержит номер минимального элемента в векторе a
m=mean(a)	Вычисление среднего арифметического элементов вектора a
a1=sort(a)	Упорядочение элементов вектора a по возрастанию
[a1,ind]=sort(a)	Второй выходной аргумент ind является вектором из целых чисел от 1 до length(a), который соответствует проделанным перестановкам

Полный список имеющихся функций выводится в командное окно при помощи команды help datafun, а для получения подробной информацию о каждой функции требуется указать ее имя в качестве аргумента команды help. Обратите внимание на то, что ряд функций допускает обращение к ним как с одним, так и с двумя выходными аргументами. В случае нескольких выходных аргументов они заключаются в квадратные скобки и отделяются запятой.

Очень часто требуется обработать только часть вектора, или обратиться к некоторым его элементам. Разберем правила MatLab, по которым производится индексация векторных данных. Для доступа к элементу вектора необходимо указать его номер в круглых скобках сразу после имени переменной, в которой содержится вектор. Например, сумма первого и третьего элементов вектора y находится при помощи выражения

Пример 3.1-21

>>s=y(1)+y(3); >>

Обращение к последнему элементу вектора можно произвести с использованием аргумента end, то есть y(end) и y(length(v)) приводят к одинаковым результатам.

Указание номеров элементов вектора можно использовать и при вводе векторов, последовательно добавляя новые элементы (не обязательно в порядке возрастания их номеров).

Пример 3.1-22

>>h=10; >>h(2)=20; >>h(4)=40 h = 10 20 0 40 >>

Заметим, что для ввода первого элемента h не обязательно указывать его индекс, так как при выполнении оператора h=1 создается вектор (массив размера один на один). Следующие операторы присваивания приводят к автоматическому увеличению длины вектора h, а пропущенные элементы (в нашем случае h(3)) получают значение ноль.

Индексация двоеточием позволяет выделить идущие подряд элементы в новый вектор. Начальный и конечный номера указываются в круглых скобках через двоеточие, например:

Пример 3.1-23

>>z=[0.2 -3.8 7.9 4.5 7.2 -8.1 3.4]; >>znew=z(3:6) znew = 7.9000 4.5000 7.2000 -8.1000 >>

Применение встроенных функций обработки данных к некоторым последовательно расположенным элементам вектора не представляет труда. Следующий вызов функции prod() вычисляет произведение элементов вектора z со второго по шестой:

Пример 3.1-24

>>p=prod(z(2:6)) >>

Индексация векторов служит для выделения элементов с заданными индексами в новый вектор. Индексный вектор должен содержать номера требуемых элементов, например:

Пример.3.1-25

>>ind=[3 5 7]; >>znew=z(ind) znew = 7.9000 7.2000 3.4000 >>

Для нахождения суммы элементов произвольного вектора z с четными индексами необходимо выполнить следующие команды:

Пример 3.1-26

>>ind=2:2:length(z); >>s=sum(z(ind)) >>

К

Конструирование новых векторов из элементов имеющихся векторов производится при помощи квадратных скобок. Следующий оператор приводит к образованию вектора, в котором пропущен пятый элемент вектора z.

Пример 3.1-27

>>znew=[z(1:4) z(6:end)] znew = 0.2000 -3.8000 7.9000 4.5000 -8.1000 3.4000 >>

Для определения матрицы необходимо задать значение элементов строк и разделить строки матрицы символом - ;, заключенными в квадратные скобки:

А=[v1;v2;v3], где v1, v2, v3 -векторы одинаковой размерности.

Кроме того для определения матриц существует множество функций. Некоторые из них приведены в табл. 3.1-7.

Таблица. 3.1-7

Функция	Результат и примеры вызовов
zeros	Нулевая матрица F=zeros(4,5) F=zeros(3) F=zeros([3 4])
eye	Единичная прямоугольная матрица (единицы расположены на главной диагонали) I=eye(5,8) I=eye(5) I=eye([5 8])
ones	Матрица, целиком состоящая из единиц E=ones(3,5) E=ones(6) E=ones([2 5])
rand	Матрица, элементы которой — случайные числа, равномерно распределенные на интервале (0,1) R=rand(5,7) R=rand(6) R=rand([3 5])
randn	Матрица, элементы которой — случайные числа, распределенные по нормальному закону с нулевым средним и дисперсией, равной единице N=randn(5,3) N=randn(9) N=randn([2 4])
diag	1) диагональная матрица, элементы которой задаются во входном аргументе – векторе D=diag(v) 2) диагональная матрица со смещенной на k позиций диагональю (положительные k — смещение вверх, отрицательные — вниз), результатом является квадратная матрица размера length(v)+abs(k) D=diag(v,k) 3) выделение главной диагонали из матрицы в вектор d=diag(A) 4) выделение k-ой диагонали из матрицы в вектор d=diag(A,k)

Рассмотрим примеры формирования матриц.

Пример 3.1-28

>>Z=zeros(3,5)Z = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>>A=[1 2 3 4; 5 6 7 8; 9 10 11 12] ; %матрица А(4х3)A = 1 2 3 4 5 6 7 8 9 10 11 12 >>

Причем элементами матрицы могут быть матрицыиливектора.

Пример 3.1-29

% первая "строка" матрицы К–матрица А, % вторая – вектор [1 2 3 4]>>K=[A;1 2 3] K = 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 >>

Таким образом, как нам уже известно, вектор является матрицей с числом строк или столбцов равным 1,а число – матрица из одного элемента:

Пример 3.1-30

>>x=[1 2 3 4]x = 1 2 3 4>>c=1.256c = 1.2560 >>

Над матрицами и элементами матрицы можно выполнять различные операции, но при этом необходимо учитывать правила работы с матрицами. Рассмотрим примеры этих операций.

1)Умножение матрицы A на матрицу B:

Пример.3.1-31

>>B=[2 5; 6 4; 6 5; 8 3]B = 2 5 6 4 6 5 8 3>>C=A*BC = 64 40 152 108 240 176 >>

2)Умножение соответствующих элементов матриц необходимо использовать оператор поэлементного доступа ".":

Пример 3.1-32

>>A1=[1 3 4 6; 9 7 4 0; 8 6 3 9];>>С2=A.*A1С2 = 1 6 12 24 45 42 28 0 72 60 33 108>>

3) Добавление элементов ("увеличение матрицы"):

Пример 3.1-33

>>a1=[A;x]a1 = 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 >>

Пара квадратных скобок при этом является оператором объединения.

4) Транспонирование матрицы (апостроф - ' ):

Пример 3.1-34

>>Bt=B'Bt = 2 6 6 8 5 4 5 3 >>

5) Удаление строки (столбца матрицы), в примере удален второй столбец:

Пример 3.1-35

>>A(:,2)=[ ] %круглые скобки – оператор извлеченияA = 1 3 4 5 7 8 9 11 12 >>

6) Извлечение элементаматрицы:

Пример 3.1-36

>>y=A(3,3) %обращение к элементу в 3-й строке и 3-м столбцеy = 12>> % или >> A(5) %обращение по номеру так, %если записать все столбцы матрицы друг за другом> ans = 7

7) Извлечение строк или столбцовматрицы:

Для извлечения строк или столбцов вместо номера элементов в строке или столбце используется двоеточие, которое является оператором перечисления (с первого до последнего элемента строки или столбца):

Пример 3.1-37

>>%извлечение 3-й строки из А, >>%двоеточие означает весь набор чисел >>y=A(3,:) y = 9 11 12 >>% в этом примере это элементы из 3-й стоки и 1 2 3 столбцов.

Двоеточие, поставленное между двумя числами – это перечисление от одного до другого числа, с указанным интервалом (по умолчанию 1):

Пример 3.1-38

>>x=0:5 %вектор х = (0 1 2 3 4 5)x = 0 1 2 3 4 5 >>x=0:0.1:0.5 %вектор х = (0 0,2 0,3 0,4 0,5)x = 0 0.1000 0.2000 0.3000 0.4000 0.5000 >>

Таким образом, матрицы небольших размеров удобно вводить из командной строки. Существует четыре способа ввода матриц. Например, необходимо определить следующую матрицу:

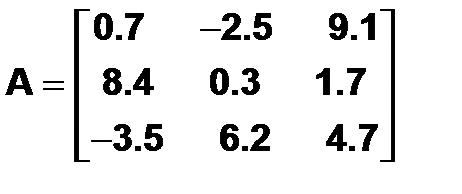
Первый способ предполагает набрать в командной строке (разделяя элементы строки матрицы пробелами): A=[0.7 –2.5 9.1 и нажать <Enter>. Курсор перемещается в следующую строку (символ приглашения командной строки >> отсутствует). Элементы каждой следующей строки матрицы набираются через пробел, а ввод строки завершается нажатием на <Enter>. При вводе последней строки в конце ставится закрывающая квадратная скобка:

Пример 3.1-39a

>>A=[0.7 -2.5 9.1 8.4 0.3 1.7 -3.5 6.2 4.7] A = 0.7000 -2.5000 9.1000 8.4000 0.3000 1.7000 -3.5000 6.2000 4.7000 >>

Второй способ ввода матрицы основан на том, что матрицу можно рассматривать как вектор-столбец, каждый элемент которого является строкой матрицы. Поскольку точка с запятой используется для разделения элементов вектора-столбца, то ввод, к примеру, матрицы

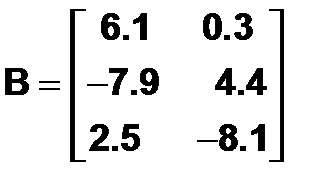осуществляется оператором присваивания:

Пример 2.3.1-39b

>>B=[6.1 0.3; -7.9 4.4; 2.5 -8.1] B = 6.1000 0.3000 -7.9000 4.4000 2.5000 -8.1000 >>

Третий способ Очевидно, что допустима такая трактовка матрицы, при которой она считается вектор-строкой, каждый элемент которой является столбцом матрицы. Следовательно, для ввода матрицы

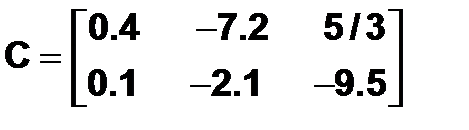достаточно воспользоваться командой:

Пример 3.1-40

>> C=[[0.4; 0.1] [-7.2; -2.1] [5.3; -9.5]] C = 0.4000 -7.2000 5.3000 0.1000 -2.1000 -9.5000 >>

Еще можно воспользоваться командой whos для получения информации о переменных A, B и C рабочей среды. В командное окно выводится таблица с информацией о размерах массивов, памяти, необходимой для хранения каждого из массивов, и типе – double array:

Пример 3.1-41

>>whos A B C Name Size Bytes Class A 3x3 72 double array B 3x2 48 double array C 2x3 48 double array >>

Функция size()позволяет установить размеры массивов, она возвращает результат в виде вектора, первый элемент которого равен числу строк, а второй – столбцов:

Пример 3.1-42

>>s=size(B) s = 3 2 >>

Сложение и вычитание матриц одинаковых размеров производится с использованием знаков +, -. Звездочка * служит для вычисления матричного произведения, причем соответствующие размеры матриц должны совпадать.

Допустимо умножение матрицы на число и числа на матрицу, при этом происходит умножение каждого элемента матрицы на число и результатом является матрица тех же размеров, что и исходная. Апостроф - ' предназначен для транспонирования вещественной матрицы или нахождения сопряженной к комплексной матрице. Для возведения квадратной матрицы в степень применяется знак ^.

MatLabобладает многообразием различных функций и способов для работы с матричными данными. Для обращения к элементу двумерного массива следует указать его номер строки и номер столбца в круглых скобках после имени массива.

Индексация двоеточием позволяет получить часть матрицы — строку, столбец или блок, например:

Пример 3.1-43

>>c1=A(2:3,2) c1 = 0.3000 6.2000 >> r1=A(1,1:3) r1 = 0.7000 -2.5000 9.1000 >>

Для обращения ко всей строке или всему столбцу не обязательно указывать через двоеточие начальный (первый) и конечный индексы, то есть операторы r1=A(1,1:3) и r1=A(1,:) эквивалентны. Для доступа к элементам строки или столбца от заданного до последнего можно использовать end, так же как и для векторов: A(1,2:end). Выделение блока, состоящего из нескольких строк и столбцов, требует индексации двоеточием, как по первому измерению, так и по второму.

Пусть в массиве T хранится матрица:

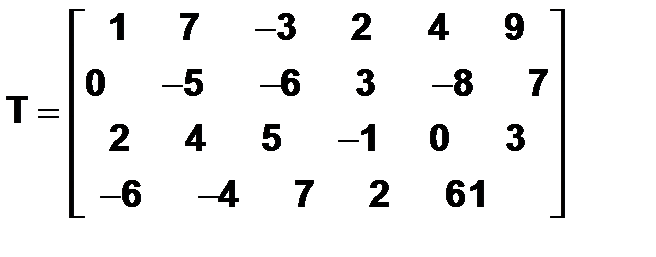
Для выделения элементов матрицы T со второй строки по третью и со второго столбца по четвертый, достаточно использовать оператор:

Пример 3.1-44

>>c1=A(2:3,2) c1 = 0.3000 6.2000 >>

Ранее было описано применение поэлементных операций к векторам. Поэлементные вычисления с матрицами производятся практически аналогично, разумеется, необходимо следить за совпадением размеров матриц:

· A.*B, A./B- поэлементные умножение и деление;

· A.^p - поэлементное возведение в степень, p - число;

· A.^B- возведение элементов матрицы A в степени, равные соответствующим элементам матрицы B;

· A.'- транспонирование матрицы (для вещественных матриц A' и A.' приводят к одинаковым результатам).

Иногда требуется не просто транспонировать матрицу, но и "развернуть" ее. Разворот матрицы на 90^o против часовой стрелки осуществляет функция rot90( ):

Пример 3.1-45

>>Q=[1 2;3 4] Q = 1 2 3 4 >>R=rot90(Q) R = 2 4 1 3 >>

Допустимо записывать сумму и разность матрицы и числа, при этом сложение или вычитание применяется, соответственно, ко всем элементам матрицы. Вызов математической функции от матрицы приводит к матрице того же размера, на соответствующих позициях которой стоят значения функции от элементов исходной матрицы.

В MatLab определены и матричные функции, например, sqrtm( ) предназначена для вычисления квадратного корня. Например, найдем квадратный корень из матрицы 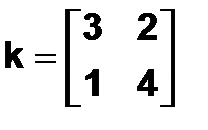и проверим полученный результат, возведя его в квадрат:

Пример 2.3.1-46

>>K=[3 2; 1 4]; >> S=sqrtm(K) S = 1.6882 0.5479 0.2740 1.9621 >>S*S ans = 3.0000 2.0000 1.0000 4.0000 >>

Матричная экспонента вычисляется с использованием expm(). Специальная функцияfunm()служит для вычисления произвольной матричной функции.

Все функции обработки данных могут быть применены и к двумерным массивам. Основное отличие от обработки векторных данных состоит в том, что эти функции работают с двумерными массивами по столбцам, например, функция sum() суммирует элементы каждого из столбцов и возвращает вектор-строку, длина, которой равна числу столбцов исходной матрицы:

Пример 3.1-47

>>M=[1 2 3; 4 5 6; 7 8 9] M = 1 2 3 4 5 6 7 8 9 >>s=sum(M) s = 12 15 18

Если в качестве второго входного аргумента sum() указать 2, то суммирование произойдет по строкам. Для вычисления суммы всех элементов матрицы требуется дважды применить sum():

Пример 3.1-48

>>s=sum(sum(M)) s = 45 >>

Очень удобной возможностью MatLab является конструирование матрицы из матриц меньших размеров. Пусть заданы матрицы:

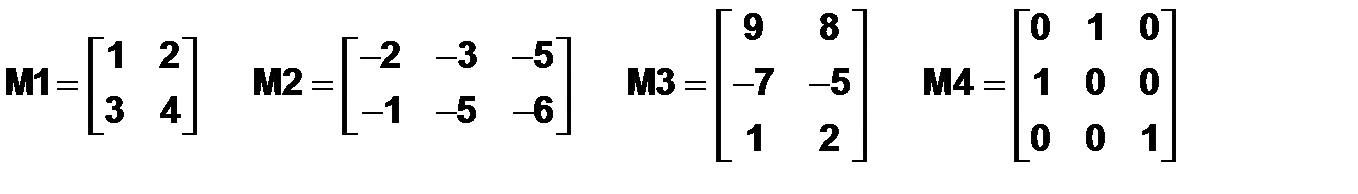
Требуется составить из M1, M2, M3и M4 блочную матрицу M

.

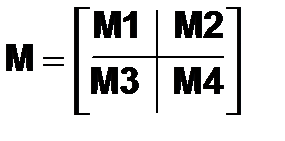Можно считать, что M имеет размеры два на два, а каждый элемент является, соответственно, матрицей M1, M2, M3или M4. Следовательно, для получения в рабочей среде MatLab матрицы M требуется использовать оператор:

Пример 2.3.1-49

>>M=[M1 M2; M3 M4]; >>

Четвертый способ. После ввода или формирования элементов векторов и матриц могут возникнуть ошибки. Для контроля и исправления отдельных элементов векторов и матриц можно воспользоваться окном редактора данных Array Editor.

ОкноArray Editor(окно редактора массива данных) состоит из панели инструментов и области просмотра значений переменных. В случае открепленного от рабочего стола окна редактирования данных в окне присутствует главное меню, которое совпадает с главным меню рабочего стола, и строка состояния (рис. 3.1-4). В окне редактора данных можно отображать не­сколько переменных. Переключение между переменными реализуется Array Editor. На
рис. 3.1-4 в окне редактирования данных находится переменная d.

Панель инструментов окна редактирования данных используется для записи данных (Save), для пе­ремещения (Cut) и копирования (Сору) в буфер обмена выделенных значений, вставки (Paste) значений из буфера и печати (Print).При перемещении выде­ленных значений в буфер обмена на их месте будут записаны нули. Количество и размерность числовых значений при вставке из буфера обмена должны сов­падать с областью, выделенной для вставки.

Рис3.1-4. Окно редактора данных