Размещение фокусов тяготения населения города

В качестве фокусов тяготения в городе выступают места приложения труда, главный городской центр, специализированные центры, места отдыха и др. Ос­новная цель — определение точки в пространстве, в которой обеспечивается минимум затрат на транспортные и пешеходные передвижения. Задача может решаться графоаналитическим, графическим и др. методами. В качестве приме­ра рассмотрим решение задачи определения оптимального местоположения го­родского центра тяготения населения графоаналитическим методом.

Суть метода заключается в определении центра тяжести территории и рас­пределения населения по этой территории, то есть точки, характеризующиеся наименьшей удаленностью от всей совокупности населения, распределенного по территории определенной конфигурации и размера. Задача решается в следую-:ией последовательности.

Оконтуривается освоенная территория, содержательно оцениваются и фик­сируются на плане элементы, корреспондирующиеся с центром. В нашем случае гаковым является население, фиксируемое на плане в виде точечной планограм-мы (рис. 6). В представленном ниже примере количество населения принято в масштабе 1 точка — 100 чел. Общее количество населения равно 100 000 чел. На точечную планограмму распределения населения наносится координатная сетка : произвольной ориентацией осей X и Y. Определяются координаты центра тяже­сти каждого квадрата сетки относительно принятой системы координат с учетом :населения каждого квадрата.

Так как координаты всех квадратов, находящихся в одном ряду (для оси Y) или в одном столбце (для оси X) одинаковы, расчет ведется в следующей после­довательности. Подсчитывается количество населения, находящегося в одном ряду (для оси Y), и полученное число умножается на координату соответствую­щего ряда. Данные заносятся в табл. 4. Полученные результаты по всем рядам суммируются и делятся на величину всего населения города. Найденное значе­ние фиксируется на соответствующей оси координат (Y) и через полученную точку проводится прямая, перпендикулярная этой оси. В той же последователь­ности расчет повторяется для оси X, для которой подсчитываются данные по всем столбцам. Точка пересечения двух построенных прямых определит поло­жение центра тяжести фигуры с учетом ее формы и распределения населения. То есть координаты центра тяжести всей фигуры с учетом распределения населения определяются из соотношений:

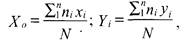
(1)

> в

— где: N — суммарное население города; щ — количество населения в каждом квадрате координатной сетки; x,,v, — координаты центров тяжести квадратов.

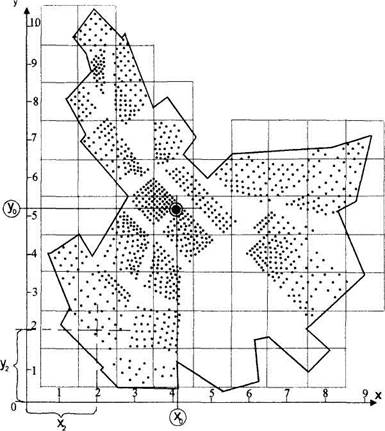Рис. 6. Определение оптимального местоположения общегородского центра тяготения населения координатным методом

Таблица 4. Определение координат центра тяжести населения

Определение координат «Х_оу>

20

Другим методом определения точки, минимизирующей затраты на передви­жения, может служить метод, основанный на гравитационном законе Рейли У. 2], суть которого заключается в определении потенциалов территорий города по критерию доступности. Согласно закону Рейли У., притягательность А_а, создава­емая точкой а, прямо пропорциональна весу точки N_a — (в нашем случае — населению) и обратно пропорциональна квадрату расстояния Ь_ам. Измеряемая в точке М сила притяжения А_ам со стороны района А равна:

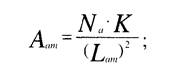m

тле: К — эмпирически определяемая постоянная.

Потенциал каждого расчетного района определяется относительно всех дру-: их районов или территорий из соотношения:

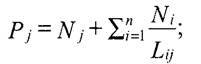(3)

де: Pj — потенциал поля расселения в точкеу; Nj — численность населения рас­четного района; /V, — численность населения района г; Ьц — расстояние между районами i и у.

Метод определения потенциалов поля расселения учитывает абсолютную численность населения и его территориальное распределение. Результаты расче-: а потенциала в каждой точке поля расселения наносятся на план города, точки . равными или близкими значениями соединяются изолиниями (рис. 7). Терри­тория, обладающая наивысшим потенциалом, наиболее предпочтительна для размещения главного городского фокуса тяготения с точки зрения минимизации атрат на передвижения. При решении задачи в качестве «веса» расчетного рай-■на, кроме численности населения, могут вводиться другие параметры — стро­ительные и эксплуатационные затраты, затраты на инженерное оборудование территории, градостроительные и эстетические характеристики площадок. В качестве расстояния может быть принято время, затрачиваемое на передвижение.

На гравитационном законе основывается и метод, предложенный Вебером А. 2] для решения задачи размещения промышленности. Задача в данном случае аключается в выборе местоположения предприятия, при котором суммарные .атраты на транспортировку сырья, его переработку и транспортировку готовой продукции, а также дальность поездок работающих на этом предприятии, будут минимальными. Метод основывается на положении: оптимальное место разме­щения производства соответствует точке в пространстве, в которой сумма издер­жек будет минимальна. Предполагается, что издержки пропорциональны рассто­янию и «весу» точек. В результате при «и» пунктов добычи сырья и «/и» — реа-:нзации готовой продукции образуется многоугольник сил, и проблема сводится ■ решению задачи классической механики. В самом первом приближении дан­ный метод может быть использован для определения точки в городе, в которой атраты на передвижения будут минимальны.

Рассмотрим наиболее простой графический способ решения задачи. Суть его аключается в следующем.

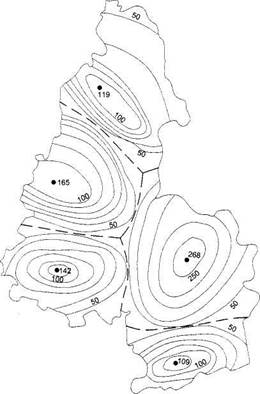1 — потенциал в точке; 2 — изолинии значений потенциала;

\У

------ 3 — границы зон влияния

Рис. 7. Распределение потенциала терри­тории по доступности

На плане фиксируются точки, являющиеся основными источниками внутриго­родских передвижений, и методом пробных точек определяется точка, в которой действие всех сил уравновешивается. Для этого строятся силовые многоугольни­ки: выбрав пробную точку, расстояния от нее до центра каждого расчетного райо­на измеряются и взвешиваются. Условно считается, что население каждого расчет­ного района сосредоточено в его геометрическом центре и определяет «вес» точ­ки — источника людского потока. Произведения расстояний от выбранной произ­вольно пробной точки до центров расчетных районов на «веса» (население) всех расчетных районов определяют длины ряда векторов, расходящихся радиально от пробной точки к центрам расчетных районов (рис. 8.1.).

Графический способ решения образованного векторами многоугольника сил заключается в том, чтобы последовательно соединить все векторы и получить результирующий, который является их равнодействующей (рис. 8.2). Выбирают­ся еще две произвольные пробные точки и относительно них повторяется та же операция. Три равнодействующие должны пересечься в одной точке, которая и будет точкой оптимального местоположения основного фокуса тяготения в пре­делах исследуемой территории (на рис. 8.2 — точка М). Этот метод в городе может применяться только для определения главного транспортного узла, каким является городской центр. В табл. 5 представлены расчетные данные для реше­ния задачи, показанной на рис. 8.

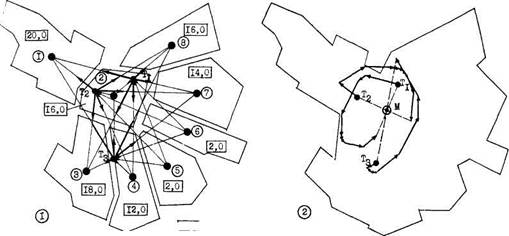© - номер района |12,0(- население района

• центр района ®М - Точка оптимального местополо-

жения центра

Рис. 8. Определение местоположения общегородского центра тяготения населения по методу Вебера А.

Таблица 5. Пример определения центра тяжести населения векторным методом

Номер	Населен.	Т		т2	Тз
района	района
	п,	L,	n,-L,	L2	n,L2	и	n,L3
		6,5		4,5		3,0
		3,5		1,5		1,0
		1,5		5,5		4,0
		1,5		5 0		5,0
		3,0		5,0		5,5
		4,0		4,0		5,5
		5,5		3,5		5,5
		7,0		3,0		5,0

Примечание: L — расстояние от пробных точек до центров расчетных районов.

Источники: 1) Якшин A.M., Говоренкова Т.М. и др. Графоаналитический метод в градострои­тельных исследованиях и проектирова­нии. — М., 1979; 2) Мерлен П. Город. Ко­личественные методы изучения. — М, 1977. Ъ)Хаггегп П. Пространственный ана­лиз в экономической географии. — М., 1968; 4) Стрельников А.И. Программа оп­ределения потенциальной транспортной потребности по воздушным расстояни­ям.— М., 1977.

23