Свойства операции сложения матриц

Определители

Определение 1.1. Пусть дана квадратная матрица 3-го порядка

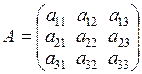. (1.1)

Определителем 3-го порядка, соответствующим матрице А (или определителем матрицы А) называется число

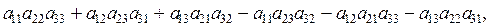
которое обозначается одним из следующих символов:

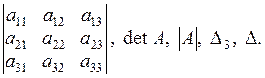
Элементы матрицы А из (1.1) называются также элементами 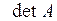. Элементы 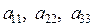образуют главную диагональ этого определителя, а элементы 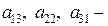его побочную диагональ.

Правило Саррюса. Определитель 3-го порядка равен сумме произве-дений его элементов, находящихся на главной диагонали и в вершинах равнобедренных треугольников, основания которых параллельны главной диагонали, минус сумма произведений элементов, находящихся на побочной диагонали и в вершинах равнобедренных треугольников, основания которых параллельны побочной диагонали (рис.1а, б).

Пример 1.1.Найти определитель матрицы А = .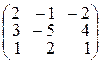

► Вычислим определитель по правилу Саррюса.

.◄

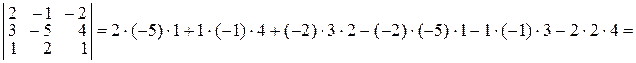
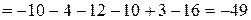Понятие определителя п-го порядка вводится индуктивно. Предположим, что введено понятие определителя для квадратной матрицы k-го порядка, 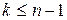, как функции, ставящей в соответствие этой матрице некоторое вещественное число. Рассмотрим квадратную матрицу п-го порядка

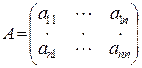. (1.2)

Если из матрицы А удалить элементы i-й строки и j-го столбца, 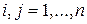, то получим квадратную матрицу 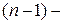го порядка, существование определителя у которой предположено выше. Назовем этот определитель минором (дополнительным минором) элемента 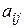матрицы А, находящегося на пересечении i-й строки и j-го столбца. Минор элемента 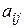будем обозначать 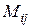. Алгебраическим дополнением элемента 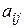назовем число .

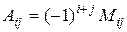Определение 1.2. Определителем п-го порядка, соответствующим матрице А из (1.2), называется число, равное 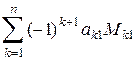и обозначаемое одним из символов: .

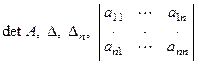Свойства определителя п-го порядка

1. Если матрица А из (1.2) содержит две одинаковых строки (или столбца), то .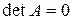

2. Если элементы какой-либо строки (или столбца) матрицы А являются суммами двух слагаемых, то 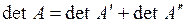, где

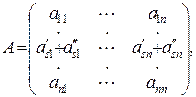
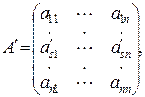
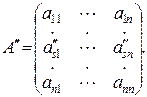
3.Общий множитель элементов какой-либо строки (или столбца) матрицы А можно выносить за знак определителя.

4. 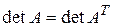, где А – матрица из (1.2), а 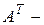матрица, полученная из А заменой строк на столбцы, то есть

.

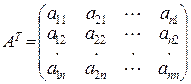Замечание 2.1. Замена строк столбцами называется операцией транспонирования матрицы, а сама матрица 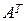называется транспонированной по отношению к матрице А.

5.Определитель единичной матрицы 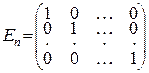равен 1.

6. При перестановке двух любых строк (или столбцов) в матрице А из (1.2) для полученной матрицы 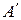справедливо равенство .

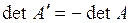7. Определитель матрицы А не меняется, если к элементам какой-либо строки (или столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Теорема1.1(о разложении определителя п-го порядка по элементам какой-либо строки или столбца). Определитель матрицы А из (1.2) равен сумме произведений элементов его любого столбца (или строки) на их алгебраические дополнения.

Замечание 1.2. Определители n-го порядка можно вычислять, например, с помощью теоремы 1.1, сводя их к определителям более низкого порядка, или при помощи свойств определителя. При этом с помощью элементарных преобразований (см. свойства 3, 6, 7) определитель приводят к верхнему треугольному виду:

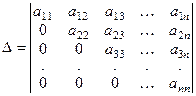, (1.3)

из теоремы 1.1 следует, что 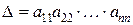, то есть определитель из (1.3) равен произведению элементов, стоящих на его главной диагонали.

Пример 1.2. Вычислить определитель .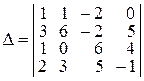

►Способ 1. Вычислим определитель Δ, используя разложение по третьей строке:

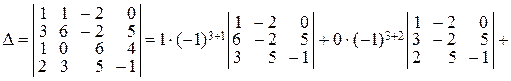
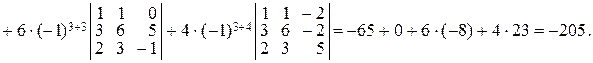
Получающиеся при разложении определители третьего порядка можно вычислить, например, по правилу Саррюса.

Способ 2. Вычислим определитель Δ, приведя его к верхней треугольной форме, используя свойства определителя. Для этого выполним следующие преобразования:

q Из второй, третьей и четвертой строк вычтем первую, умноженную соответственно на 3, 1, 2:

.

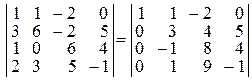q Переставим вторую и четвертую строки, при этом определитель по-меняет знак:

.

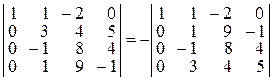q К третьей строке полученного определителя прибавим вторую, а из последней строки вычтем вторую, умноженную на 3:

.

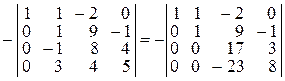q К третьему столбцу прибавим последний, умноженный на 3:

.

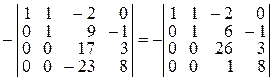q Переставим две последние строки:

.

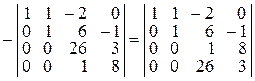q Из последней строки вычтем третью, умноженную на 26:

.

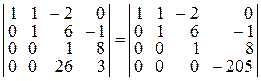q Полученный в результате определитель является определителем от верхней треугольной матрицы, он равен произведению элементов, стоящих на главной диагонали:

◄

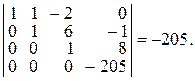§2. Действия с матрицами

Определение 2.1.Матрицей называется прямоугольная таблица чисел, обозначаемая следующим образом: .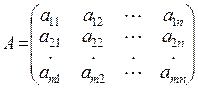

Матрица А содержит т строк и п столбцов. Говорят, что она имеет размер 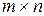, для неё принято также обозначение .

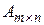Определение 2.2.Суммой двух матрицА и В одинакового размера 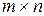называется матрица С того же размера, элементы которой есть суммы соответствующих элементов матриц слагаемых, то есть

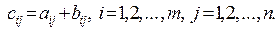
Принято обозначение 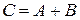, поэтому, если

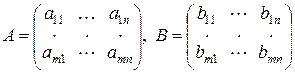, то .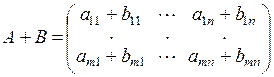

Свойства операции сложения матриц

1. 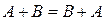– коммутативность (переместительный закон) сложения.

2. 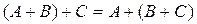– ассоциативность (сочетательный закон) сложения.

Определение 2.3.Произведением матрицы А на вещественное число λ называется матрица того же размера, обозначаемая 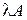, элементы которой есть произведения соответствующих элементов матрицы А на это число λ.

Таким образом, .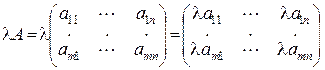

Сложение матриц и умножение матрицы на число называются линейными операциями с матрицами

Пример 2.1.Даны две матрицы: А и В. Найти матрицу 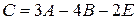, еслиA = 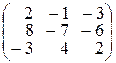, B = 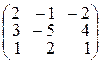, Е – единичная матрица.

►

.◄

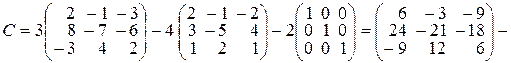
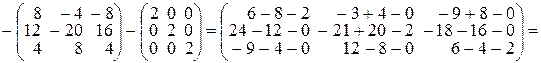
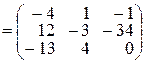Определение 2.4.Произведением матрицы А размера 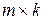на матрицу В размера 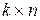называется матрица С размера 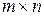, элемент которой 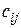, находящийся в i-ой строке и в j-ом столбце, равен сумме произведений соответствующих элементов i-ой строки матрицы А и j-ого столбца матрицы В:

.

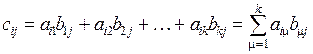Принято обозначение С=АВ. Рассмотрим частный случай произведения матрицы-строки на матрицу-столбец:

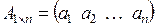и .

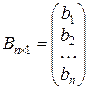Матрица 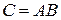имеет размер 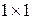, причём её элемент 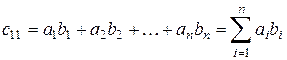. Таким образом,

.

j

А

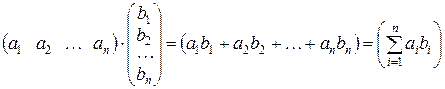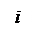
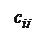
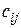Правило для вычисления произведения матриц схематично изображено на рис. 2.1. При умножении матриц обычно говорят, что элемент матрицы 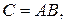стоящий в i-ой строке и в j-ом столбце, является «произведением i-ой строки матрицы А и j-го столбца матрицы В».