Задачи для самостоятельного решения. 1. Найти смешанное произведение векторов
1. Найти смешанное произведение векторов 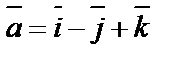 ,
, 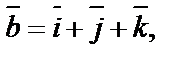
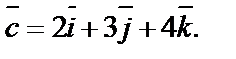
2. Показать, что векторы 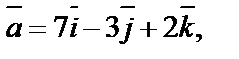
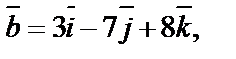
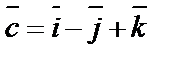 компланарны.
компланарны.
3. Доказать, что точки 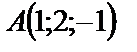 ,
, 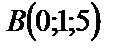 ,
, 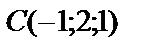 ,
, 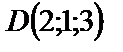 лежат в одной плоскости.
лежат в одной плоскости.
4. Найти объем параллелепипеда, построенного на векторах 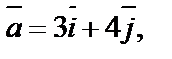
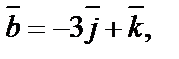
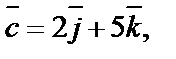 как на ребрах.
как на ребрах.
5. Дана пирамида с вершинами О(0;0;0), А(5;2;0), В(2;5;0) и С(1;2;4). Найдите её объем, площадь грани АВС и длину высоты, опущенной на эту грань.
Ответы. 1. 4. 4. 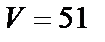 . 5.
. 5. 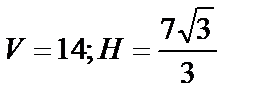 .
.
2.9. Прямая на плоскости
Линия на плоскости рассматривается (задается) как множество точек, обладающих некоторым, только им присущим геометрическим свойством.
Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел - ее координат, а положение линии на плоскости определять с помощью уравнения (то есть равенства, связывающего координаты точек линии).
Определение. Уравнением линии (или кривой) на плоскости Oxy называется такое уравнение 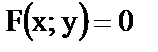 с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Переменные x и у в уравнении линии называются текущими координатами точек линии.
Пример 24. Лежат ли точки 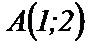 и
и 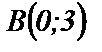 на линии
на линии 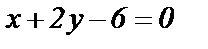 ?
?
Решение.Подставив в уравнение линии вместо x и у координаты точки А, получим 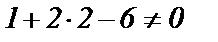 . Значит точка А не лежит на данной линии.
. Значит точка А не лежит на данной линии.
Подставим в уравнение линии координаты точки В вместо x и у 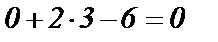 . Следовательно, точка В лежит на данной линии.
. Следовательно, точка В лежит на данной линии.
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разнее виды уравнений прямой.
Пусть 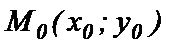 - заданная точка прямой l. Вектор
- заданная точка прямой l. Вектор 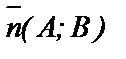 , перпендикулярный прямой l, называют нормальным вектором прямой. Пусть
, перпендикулярный прямой l, называют нормальным вектором прямой. Пусть 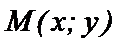 - произвольная (текущая) точка прямой. l. Тогда
- произвольная (текущая) точка прямой. l. Тогда 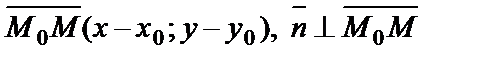 .
.
По свойствам скалярного произведения 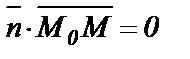 , то есть
, то есть
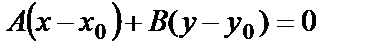 . (55)
. (55)
Полученное уравнение называется уравнением прямой, проходящей через данную точку перпендикулярно данному вектору.
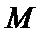 |
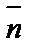 |
| l |
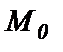 |
 |
Раскрыв скобки и сгруппировав слагаемые в (55), получим 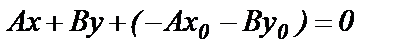 . Обозначим
. Обозначим 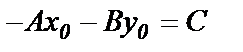 , уравнение (2.25) примет вид
, уравнение (2.25) примет вид
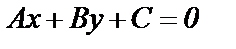 , (56)
, (56)
которое называется общим уравнением прямой на плоскости.
Некоторые частные случаи общего уравнения прямой:
1) если 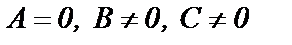 , то уравнение приводится к виду
, то уравнение приводится к виду 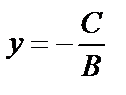 . Это есть уравнение прямой, параллельной оси Ох;
. Это есть уравнение прямой, параллельной оси Ох;
2) если 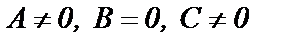 , то уравнение приводится к виду
, то уравнение приводится к виду 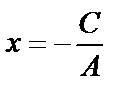 , прямая параллельна оси Оу;
, прямая параллельна оси Оу;
3) если 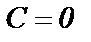 ,
, 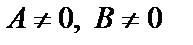 , то получим
, то получим 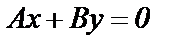 , прямая проходит через начало координат;
, прямая проходит через начало координат;
4)если 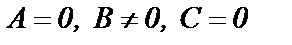 , уравнение прямой принимает вид
, уравнение прямой принимает вид 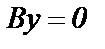 или
или 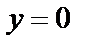 , прямая проходит через ось Ох;
, прямая проходит через ось Ох;
5)если 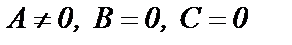 , уравнение прямой
, уравнение прямой 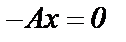 , или х=0, прямая проходит через ось Оу.
, или х=0, прямая проходит через ось Оу.
Пусть в уравнении (56) 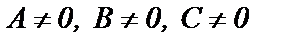 , тогда перенесем слогаемое С в правую часть и разделим на него обе части уравнения
, тогда перенесем слогаемое С в правую часть и разделим на него обе части уравнения
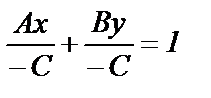 , или
, или 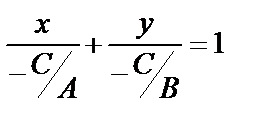 .
.
Обозначив 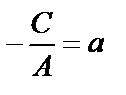 ,
, 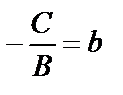 , получим уравнение
, получим уравнение
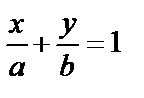 , (57)
, (57)
которое называется уравнением прямой в отрезках, здесь а и b
отрезки, отсекаемые прямой на осях координат.
| а |
| b |
| l |
| x |
| y |
| O |
Определение. Вектор 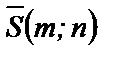 , паралельный прямой, называется направляющим вектором прямой.
, паралельный прямой, называется направляющим вектором прямой.
| l |
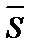 |
Пусть 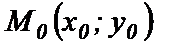 - заданная точка на прямой l,
- заданная точка на прямой l, 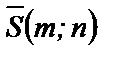 - направляющий вектор этой прямой,
- направляющий вектор этой прямой, 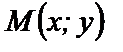 - произвольная точка прямой l.
- произвольная точка прямой l.
| l |
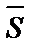 |
 |
 |
| M |
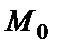 |
Тогда 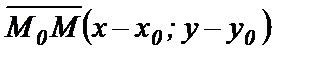 ,
, 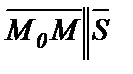 . Используя условие (53), получим:
. Используя условие (53), получим:
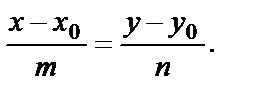 (58)
(58)
Полученное уравнение (58) называется каноническим уравнением прямой, или уравнением прямой, проходящей через данную точку параллельно данному вектору.
В частности, если прямая 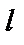 параллельна оси Ох, то ее направляющий вектор
параллельна оси Ох, то ее направляющий вектор 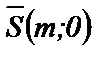 и уравнение (58) имеет вид
и уравнение (58) имеет вид 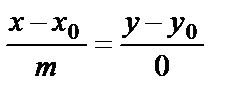 , или
, или 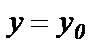 .
.
Если 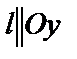 , то
, то 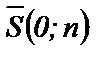 и уравнение прямой
и уравнение прямой 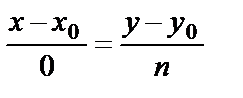 , или
, или 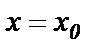 .
.
Если в уравнении (58) величину отношения положить равной 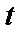
( 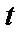 - параметр, переменная величина,
- параметр, переменная величина, 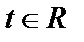 ):
): 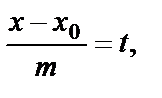
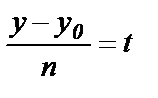 , то, выразив х и у из уравнений, получим
, то, выразив х и у из уравнений, получим
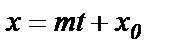 ,
, 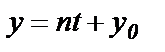 . (59)
. (59)
Уравнения (59) называются параметрическими уравнениями прямой.
Пусть на прямой 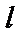 заданы две точки
заданы две точки 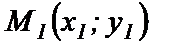 и
и 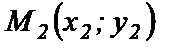 . Тогда вектор
. Тогда вектор 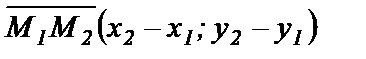 является направляющим вектором прямой и, используя уравнение (58), можно записать
является направляющим вектором прямой и, используя уравнение (58), можно записать
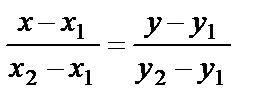 . (60)
. (60)
Уравнение (60) - уравнение прямой, проходящей через две данные точки.
Пусть 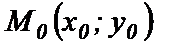 - заданная точка на прямой l,
- заданная точка на прямой l, 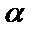 - угол наклона прямой к оси Ох,
- угол наклона прямой к оси Ох, 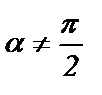 . В качестве направляющего вектора прямой l возьмем единичный вектор
. В качестве направляющего вектора прямой l возьмем единичный вектор 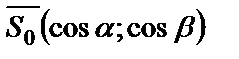 , но
, но 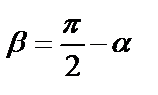 , тогда
, тогда 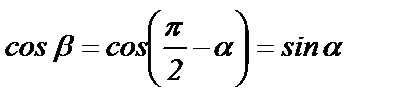 , то есть
, то есть 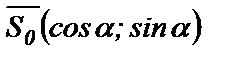 . Используя уравнение (58), получим
. Используя уравнение (58), получим 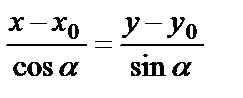 или
или 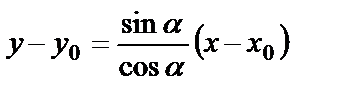 . Обозначим
. Обозначим 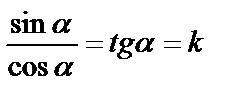 (k - угловой коэффициент прямой), получим уравнение прямой, проходящей через данную точку в заданном направлении
(k - угловой коэффициент прямой), получим уравнение прямой, проходящей через данную точку в заданном направлении
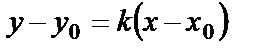 . (61)
. (61)
 |
 |
 |
| x |
| y |
| b |
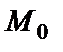 |
| l |
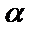 |
| O |
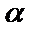 |
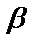 |
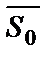 |
Выразив из (61) у: 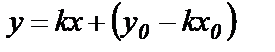 и обозначив
и обозначив 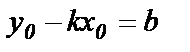 , получим уравнение
, получим уравнение
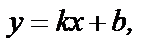 (62)
(62)
которое называется уравнением прямой с угловым коэффициентом. В уравнении (62) b - ордината точки пересечения прямой с осью Оу.
2.9.1.Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых.
Пусть прямые 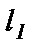 и
и 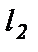 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами 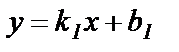 и
и 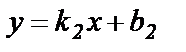 , где
, где 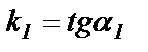 ,
, 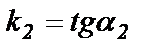 .
.
Требуется найти угол 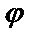 , на который надо повернуть в положительном направлении прямую
, на который надо повернуть в положительном направлении прямую 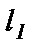 вокруг точки их пересечения до совпадения с прямой
вокруг точки их пересечения до совпадения с прямой 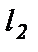 .
.
| x |
| y |
| O |
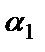  |
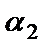 |
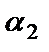 |
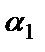  |
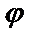 |
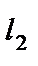 |
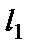 |
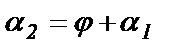 (по теореме о внешнем угле треугольника) или
(по теореме о внешнем угле треугольника) или 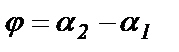 .
.
Если 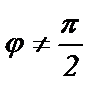 , то
, то 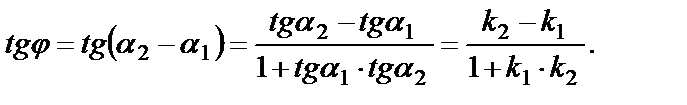
Таким образом
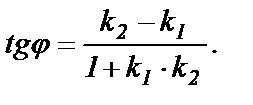 (63)
(63)
Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая - второй, то правая часть формулы (63) берется по модулю, то есть
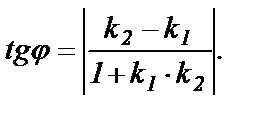 (64)
(64)
Если 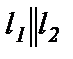 , то
, то 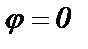 и
и 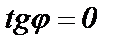 . Из формулы (63) следует, что
. Из формулы (63) следует, что 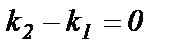 , то есть
, то есть
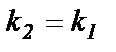 . (65)
. (65)
Если 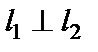 , то
, то 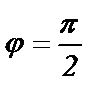 ,
, 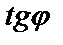 не существует. Тогда рассмотрим
не существует. Тогда рассмотрим 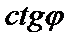 :
: 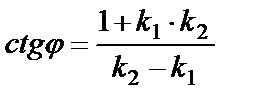 ,
, 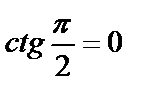 .
.
Отсюда 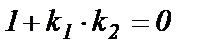 , то есть
, то есть
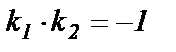 (или
(или 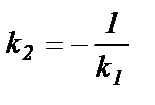 ). (66)
). (66)
Если прямые 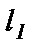 и
и 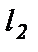 заданы общими уравнениями
заданы общими уравнениями 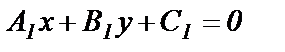 и
и 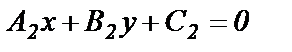 , где
, где 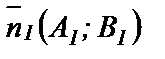 и
и 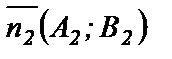 - нормальные векторы прямых, то
- нормальные векторы прямых, то
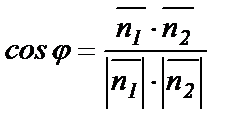 или
или
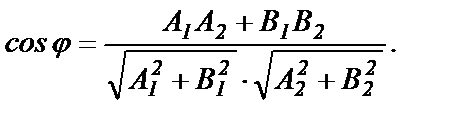 (67)
(67)
Если 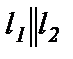 , то
, то 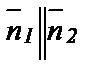 , следовательно
, следовательно
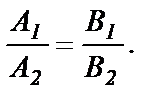 (68)
(68)
Если 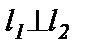 , то
, то 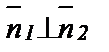 , то есть
, то есть 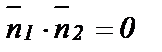
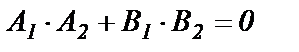 . (69)
. (69)
