Свойства смешанного произведения

1) Если в смешанном произведении перемножаемые векторы переставить в круговом порядке, то произведение не изменится:

.

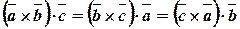2) Если в смешанном произведении поменять местами знаки векторного и скалярного умножения, то произведение не изменится:

.

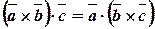Это свойство позволяет записывать смешанное произведение в виде 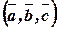без знаков векторного и скалярного умножения.

3) Перестановка в смешанном произведении любых двух векторов изменит лишь его знак:

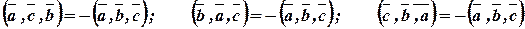
4) Смешанное произведение обращается в нуль, если:

а) хотя бы один из перемножаемых векторов есть нуль- вектор;

б) два из перемножаемых векторов коллинеарные;

в) три перемножаемые вектора компланарны;

Заметим, что случай в) содержит в себе и оба предыдущих: Если хотя бы один из трех векторов есть нуль-вектор или два из них коллинеарны, то все три вектора будут компланарны, следовательно,

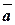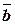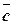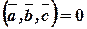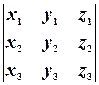, , -компланарны Û или =0.

Пример 17. Даны точки , , , .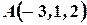

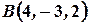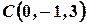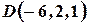Определить лежат ли точки 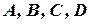в одной плоскости.

Решение. Точки будут лежать в одной плоскости, если три вектора, соединяющие эти точки, являются компланарными. Составим, например, вектора 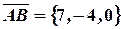, , 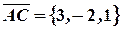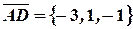и найдем их смешанное произведение:

,

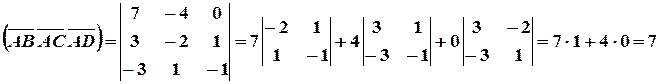Поскольку 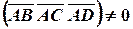, то вектора 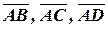не компланарны, а стало быть, точки не лежат в одной плоскости.

Пример 18. Даны точки , , , .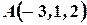

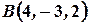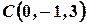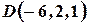Найти объем пирамиды .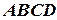

Решение. Объем пирамиды равен 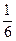части 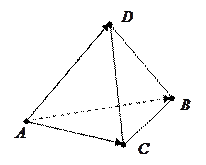объема параллелепипеда, построенного на векторах 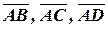, и вычисляется он по формуле:

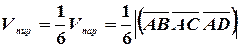
Эти три вектора имеют координаты:

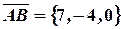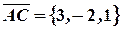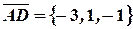, , . Их смешанное произведение будет равно:

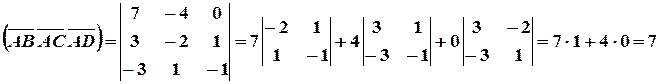
Отсюда получим V_пир= 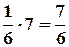(куб.ед.).

Понятие вектора обобщают и на случай 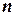- мерного пространства, только уже не физического, а, например, пространство товаров, услуг и т.д.

В этом случае под вектором понимаютупорядоченную совокупность 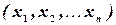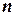- вещественных чисел и называют ее 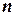- мерным вектором, а числа 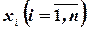- компонентами, или координатами, вектора.

Если, например, некоторый автомобильный завод должен выпустить в смену 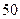легковых автомобилей, 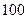грузовых, 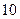автобусов, 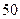комплектов запчастей для легковых автомобилей и 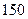комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора 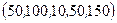, имеющего пять компонент.

В этом случае произведением вектора 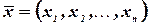на действительное число 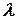называется вектор .

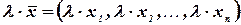Суммой векторов 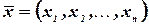и 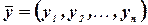называется вектор .

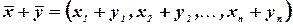Кроме того, N-мерное векторное пространство 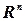определяется как множество всех 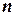- мерных векторов, для которых определены операции умножения на действительные числа и сложение.

Экономическая иллюстрация 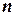- мерного векторного пространства: пространство благ (товаров). Под товаром мы будем понимать некоторое благо или услугу, поступившие в продажу в определенное время в определенном месте. Предположим, что существует конечное число наличных товаров 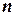. Количества каждого из них, приобретенные потребителем, характеризуются набором товаров

,

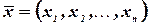где через 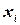обозначается количество 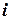- го блага, приобретенного потребителем. Будем считать, что все товары обладают свойством произвольной делимости, так что может быть куплено любое неотрицательное количество каждого из них. Тогда все возможные наборы товаров являются векторами пространства товаров .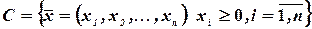