Различные виды уравнения прямой на плоскости

1.Уравнение прямой с угловым коэфициэнтом.
Определение. Уравнение прямой вида

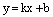
называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.

В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.

Уравнение вида

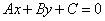
называется общим уравнением прямой.

Уравнение 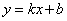называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением

,

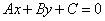то ее угловой коэффициент определяется по формуле

.

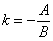Уравнение 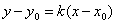является уравнением прямой, которая проходит через точку 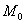( 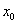, 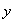) и имеет угловой коэффициент k.

Если прямая проходит через точки 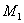( 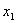, 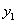), 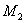( 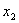, 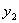), то ее угловой коэффициент определяется по формуле

.

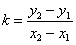Уравнение

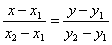
является уравнением прямой, проходящей через две точки 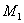( 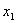,У₁ ) и М₂( , ).

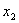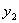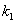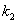Если известны угловые коэффициенты и двух прямых, то один из углов 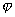между этими прямыми определяется по формуле

.

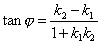Признаком параллельности двух прямых является равенство их угловых коэффициентов:

.

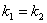Признаком перпендикулярности двух прямых является соотношение

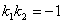, или .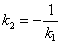

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.

Уравнение прямой в отрезка

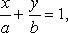
где a, b - величины отрезков, отсекаемых прямой на осях координат.

Угол между двумя прямыми

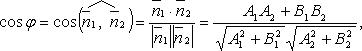
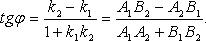
Необходимое и достаточное условие перпендикулярности двух прямых

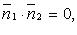или или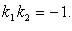

Расстояние между параллельными прямыми

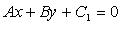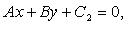Если прямые заданы уравнениями и то

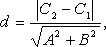
Пучок прямых

Если 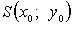- центр пучка, то уравнение пучка

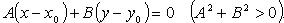
Расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

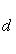
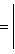
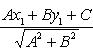
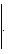
Окружность.

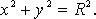Канонические уравнения

Окружность радиуса R с центром в начале координат:

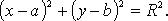Окружность радиуса R с центром в точке C(a; b):

О: Общим уравнением кривой 2-го порядка (кр. 2п) называется уравнение II степени относительно текущих координат:

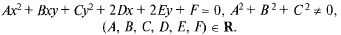(4.1)

Частным случаем уравнения кр. 2п является уравнение окружности (п. 3.1.1): 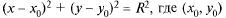— центр; R — радиус.

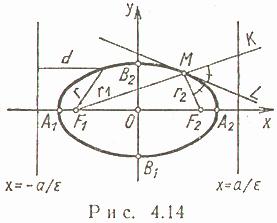
Эллипс.

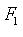
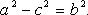Пусть на плоскости заданы две точки и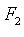 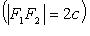и дано число a (a > c). Эллипс - множество точек M плоскости, для каждой из которых сумма расстояний от точек 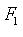и 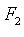равна 2a. Точк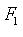и и 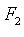называются фокусами эллипса; 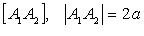- большая ось; 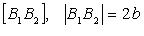- малая ось; O - центр; 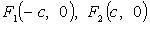- левый и правый фокусы; 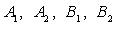- вершины; 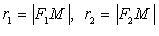- фокальные радиусы;

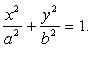
Каноническое уравнение:

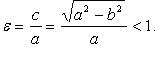
Эксцентриситет:

Уравнения директрис: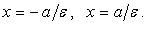

Гипербола.

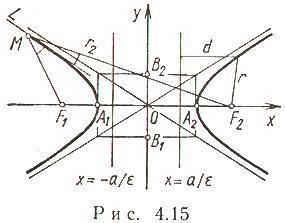
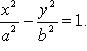Пусть на плоскости заданы две точк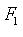и и 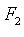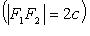и дано число a (0 < a < c). Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек 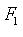и 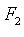равен 2a. Точк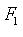и и 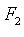называются фокусами гиперболы; 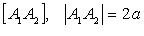- действительная ось; 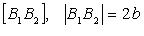- мнимая ось; O - центр; 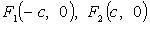- левый и правый фокусы; 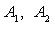- вершины; 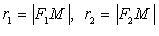- фокальные радиусы: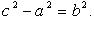

Каноническое уравнение:

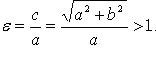
Эксцентриситет:

Фокальный параметр: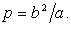

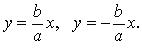
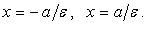Уравнения директрис:

Уравнения асимптот:

Парабола.

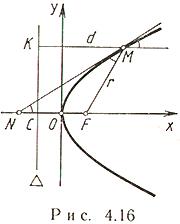
Пусть на плоскости заданы точка F и прямая 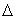, не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой 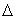. Точка F называется фокусом, прямая 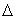- директрисой параболы; (OF) - ось, O - вершина, 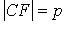- параметр, 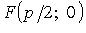- фокус, 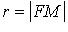- фокальный радиус.

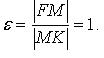Каноническое уравнение: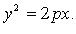

Эксцентриситет:

Уравнение директрисы: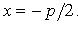

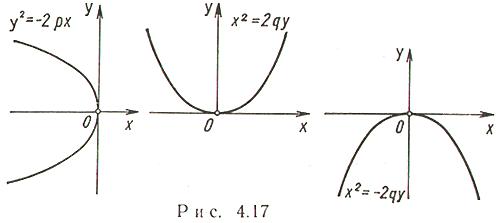
Другие формы канонического уравнения (рис. 4.17):

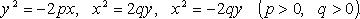
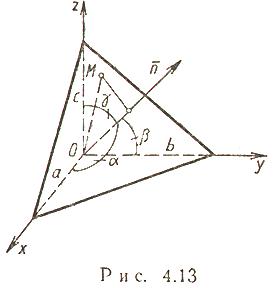Плоскость.